Delaunay三角剖分

最近在做人脸识别，在基于网格的特征提取部分遇到了Delaunay三角剖分。之前对此概念没什么印象，就查找相关资料学习，原来它是代数拓扑学里最基本的研究方法，总结如下：
转自：http://www.cnblogs.com/RenLiQQ/archive/2008/02/06/1065399.html
三角剖分与Delaunay剖分的定义
　　如何把一个散点集合剖分成不均匀的三角形网格，这就是散点集的三角剖分问题，散点集的三角剖分，对数值分析以及图形学来说，都是极为重要的一项预处理技术。该问题图示如下：

1.1.三角剖分定义
　　【定义】三角剖分：假设V是二维实数域上的有限点集，边e是由点集中的点作为端点构成的封闭线段, E为e的集合。那么该点集V的一个三角剖分T=(V,E)是一个平面图G，该平面图满足条件：
　　1.除了端点，平面图中的边不包含点集中的任何点。
　　2.没有相交边。
　　3.平面图中所有的面都是三角面，且所有三角面的合集是散点集V的凸包。
1.2. Delaunay三角剖分的定义
　　在实际中运用的最多的三角剖分是Delaunay三角剖分，它是一种特殊的三角剖分。先从Delaunay边说起：
　　【定义】Delaunay边：假设E中的一条边e（两个端点为a,b），e若满足下列条件，则称之为Delaunay边：存在一个圆经过a,b两点，圆内(注意是圆内，圆上最多三点共圆)不含点集V中任何其他的点，这一特性又称空圆特性。
　　【定义】Delaunay三角剖分：如果点集V的一个三角剖分T只包含Delaunay边，那么该三角剖分称为Delaunay三角剖分。
1.3.Delaunay三角剖分的准则
　　要满足Delaunay三角剖分的定义，必须符合两个重要的准则：
　　1、空圆特性：Delaunay三角网是唯一的（任意四点不能共圆），在Delaunay三角形网中任一三角形的外接圆范围内不会有其它点存在。如下图所示：
　　
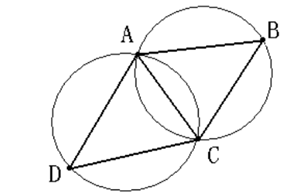
　　2、最大化最小角特性：在散点集可能形成的三角剖分中，Delaunay三角剖分所形成的三角形的最小角最大。从这个意义上讲，Delaunay三角网是“最接近于规则化的“的三角网。具体的说是指在两个相邻的三角形构成凸四边形的对角线，在相互交换后，六个内角的最小角不再增大。如下图所示：
　　
1.4.Delaunay三角剖分的特性
　　以下是Delaunay剖分所具备的优异特性：
　　　1.最接近：以最近临的三点形成三角形，且各线段(三角形的边)皆不相交。
　　　2.唯一性：不论从区域何处开始构建，最终都将得到一致的结果。
　　　3.最优性：任意两个相邻三角形形成的凸四边形的对角线如果可以互换的话，那么两个三角形六个内角中最小的角度不会变大。
　　　4.最规则：如果将三角网中的每个三角形的最小角进行升序排列，则Delaunay三角网的排列得到的数值最大。
　　　 5.区域性：新增、删除、移动某一个顶点时只会影响临近的三角形。
　　　 6.具有凸多边形的外壳：三角网最外层的边界形成一个凸多边形的外壳。
1.5.局部最优化处理
　　理论上为了构造Delaunay三角网，Lawson提出的局部优化过程LOP(Local Optimization Procedure)，一般三角网经过LOP处理，即可确保成为Delaunay三角网，其基本做法如下所示：
　　1.将两个具有共同边的三角形合成一个多边形。
　　2.以最大空圆准则作检查，看其第四个顶点是否在三角形的外接圆之内。
　　3.如果在，修正对角线即将对角线对调，即完成局部优化过程的处理。
LOP处理过程如下图所示：

2.Delaunay剖分的算法
　　Delaunay剖分是一种三角剖分的标准，实现它有多种算法。
2.1.Lawson算法
　　逐点插入的Lawson算法是Lawson在1977年提出的，该算法思路简单，易于编程实现。基本原理为：首先建立一个大的三角形或多边形，把所有数据点包围起来，向其中插入一点，该点与包含它的三角形三个顶点相连，形成三个新的三角形，然后逐个对它们进行空外接圆检测，同时用Lawson设计的局部优化过程LOP进行优化，即通过交换对角线的方法来保证所形成的三角网为Delaunay三角网。
上述基于散点的构网算法理论严密、唯一性好，网格满足空圆特性，较为理想。由其逐点插入的构网过程可知，遇到非Delaunay边时，通过删除调整，可以构造形成新的Delaunay边。在完成构网后，增加新点时，无需对所有的点进行重新构网，只需对新点的影响三角形范围进行局部联网，且局部联网的方法简单易行。同样，点的删除、移动也可快速动态地进行。但在实际应用当中，这种构网算法当点集较大时构网速度也较慢，如果点集范围是非凸区域或者存在内环，则会产生非法三角形。
2.2.Bowyer-Watson算法
Bowyer-Watson算法的基本步骤是：
　　1、构造一个超级三角形，包含所有散点，放入三角形链表。
　　 2、将点集中的散点依次插入，在三角形链表中找出其外接圆包含插入点的三角形（称为该点的影响三角形），删除影响三角形的公共边，将插入点同影响三角形的全部顶点连接起来，从而完成一个点在Delaunay三角形链表中的插入。
　　3、根据优化准则对局部新形成的三角形进行优化。将形成的三角形放入Delaunay三角形链表。
　　4、循环执行上述第2步，直到所有散点插入完毕。
这一算法的关键的第2步图示如下：

Bowyer-Watson算法伪代码如下：
伪代码思路：
subroutine triangulate
input : vertex list
output : triangle list
initialize the triangle list
determine the supertriangle
add supertriangle vertices to the end of the vertex list
add the supertriangle to the triangle list
for each sample point in the vertex list
initialize the edge buffer
for each triangle currently in the triangle list
calculate the triangle circumcircle center and radius
if the point lies in the triangle circumcircle then
add the three triangle edges to the edge buffer
remove the triangle from the triangle list
endif
endfor
delete all doubly specified edges from the edge buffer
this leaves the edges of the enclosing polygon only
add to the triangle list all triangles formed between the point
and the edges of the enclosing polygon
endfor
remove any triangles from the triangle list that use the supertriangle vertices
remove the supertriangle vertices from the vertex list
end

优化后的伪代码为：
input: 顶点列表(vertices)　　　　　　　　　　　　　　　　　　　　 　//vertices为外部生成的随机或乱序顶点列表
output:已确定的三角形列表(triangles)
　　　　初始化顶点列表
　　　　创建索引列表(indices = new Array(vertices.length))　　　　//indices数组中的值为0,1,2,3,…,vertices.length-1
　　　　基于vertices中的顶点x坐标对indices进行sort　　 　　　　　 //sort后的indices值顺序为顶点坐标x从小到大排序（也可对y坐标，本例中针对x坐标）
　　　　确定超级三角形
　　　　将超级三角形保存至未确定三角形列表（temp triangles）
　　　　将超级三角形push到triangles列表
　　　　遍历基于indices顺序的vertices中每一个点　　　　　　　　　 　//基于indices后，则顶点则是由x从小到大出现
　　　　　　初始化边缓存数组（edge buffer）
　　　　　　遍历temp triangles中的每一个三角形
　　　　　　　　计算该三角形的圆心和半径
　　　　　　　　如果该点在外接圆的右侧
　　　　　　　　　　则该三角形为Delaunay三角形，保存到triangles
　　　　　　　　　　并在temp里去除掉
　　　　　　　　　　跳过
　　　　　　　　如果该点在外接圆外（即也不是外接圆右侧）
　　　　　　　　　　则该三角形为不确定 　　　　　　　　　 //后面会在问题中讨论
　　　　　　　　　　跳过
　　　　　　　　如果该点在外接圆内
　　　　　　　　　　则该三角形不为Delaunay三角形
　　　　　　　　　　将三边保存至edge buffer
　　　　　　　　　　在temp中去除掉该三角形
　　　　　　对edge buffer进行去重
　　　　　　将edge buffer中的边与当前的点进行组合成若干三角形并保存至temp triangles中
　　　　将triangles与temp triangles进行合并
　　　　除去与超级三角形有关的三角形
end