深度学习00

Regression

Gradient Descent

learning rate的取值很重要，一般会绘制右图，横轴为迭代次数，纵轴为loss。从图中可以看到learning rate太小迭代的速度太慢，太大可能無法收斂。如何加快训练速度？

Tips1：Adagrad—选择合适的步伐
学习率除以前面几次一阶导平方和的均值

$\frac{{\eta }^t}{{\sigma }^t}=\frac{\eta }{\sqrt{t+1}}\ast \frac{\sqrt{t+1}}{\sqrt{\sum _{i=0}^t(g^i{)}^2}}=\frac{\eta }{\sqrt{\sum _{i=0}^t(g^i{)}^2}}$


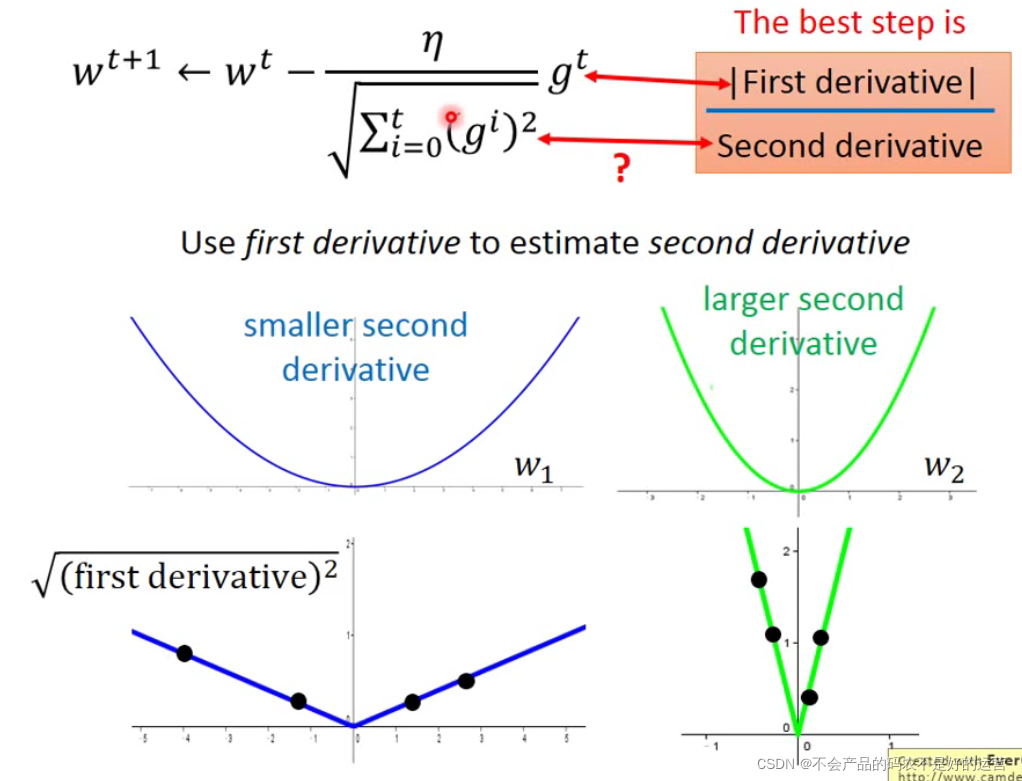
Adagrad中“梯度越大，step不一定越大”，最好的步伐是 $\frac{|一次微分|}{二次微分}$,可用这个比值衡量几个点距离极值点的远近。$g^t$是一次微分，$\sqrt{\sum _{i=0}^t(g^i{)}^2}$反应了二次微分的大小

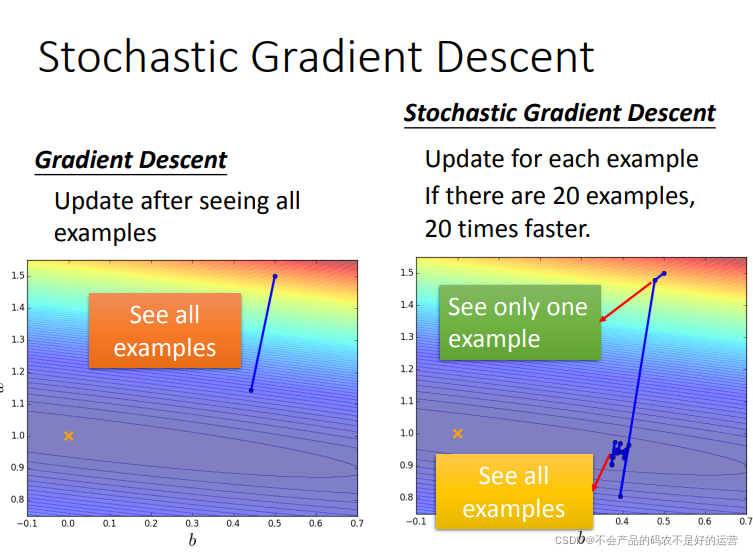
Tips2：SGD：随机梯度下降
随机选一个样本迭代参数

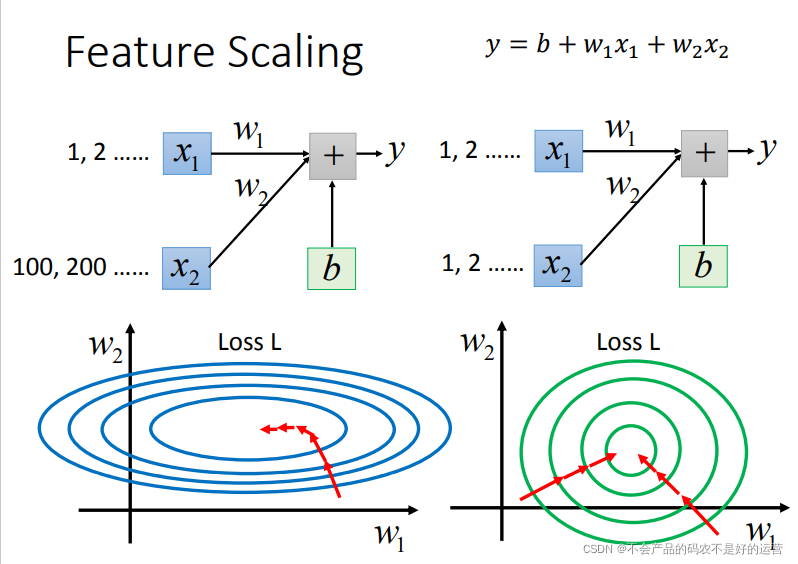
Tips3：特征放缩（Feature Scaling）归一化参数
从下图可以看出，如果没做归一化，w2小小的变化，loss就下降了一圈，而w1只能走很大一步，loss才下降一圈。

Gradient Descent theory

梯度下降可以看作是损失函数的一阶近似，近似的前提是图中的红色圆圈足够小



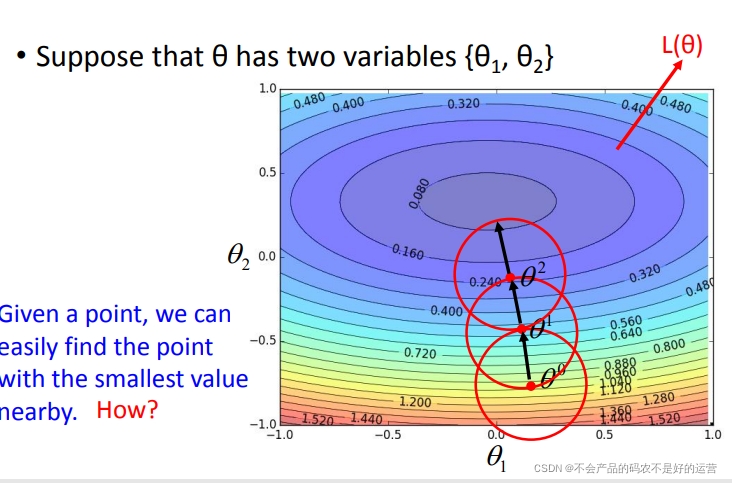
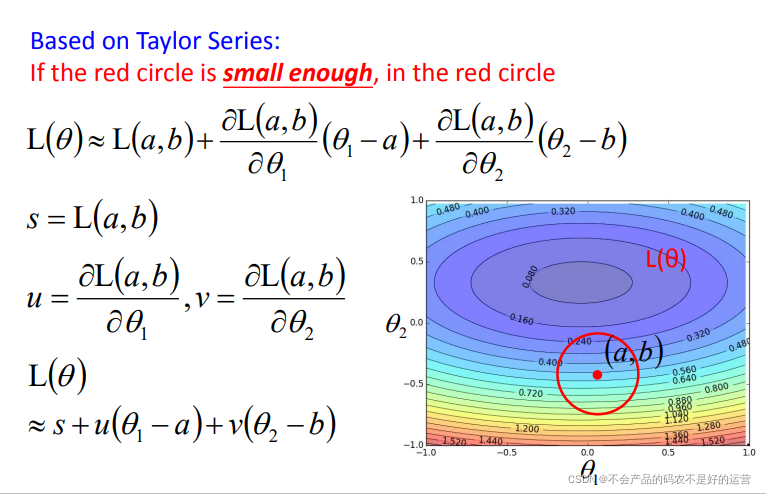
如果对一阶展开不满意，可以尝试二阶展开如Newton’s method，但是二阶所需要的计算量很大，因此一般都用一阶。

Classification

Q：能否将分类问题直接当作回归问题来解？（即分类问题直接用回归的损失函数）
A：
1、容易受到异常值的影响，如下右图中右下角有一堆离得非常远的点，其实我们可以看出绿色线是分类比较好的，但是因为要使得均方误差减少，故绿色线会变成紫色线。

2、多分类的时候，把类别1变成数值1，类别2变成数值2，类别3变成数值3……暗示类别1与类别2比较接近，与类别3比较远，实际上并无此关系。

那应该如何做呢？
一个替代方案是：

以二分类，将function中内嵌一个函数g(x)，如果大于0，就认识是类别1，否则认为是类别2。损失函数的定义就是，如果选中某个funciton f，在训练集上预测错误的次数。当然希望错误次数越小越好。但是这样的损失函数没办法解，这种定义没办法微分。

two boxes

将上面两个盒子换成两个类别：
若知道红色方框的值，就可以计算出给一个x，它是属于哪个类型的，P(C1|x) 和 P(C2x) ，谁大就属于谁。接下来就需要从训练集中估测红色方框中的值

1、其中$P(x)$为全概率公式，$P(C1|x)$为贝叶斯公式)
2、这一套想法叫做 Generative Model。因为有了这个model，就可以生成一个x，可以计算某个x出现的几率，知道了x的分布，就可以自己产生x

Prior 先验

知道了P(C1)和P(C2)，下面求解$P(x|C1)$：

这里假设这79点是从高斯分布（Gaussian distribution）中得到的，现在需要从这79个点找出符合的那个高斯分布。

高斯分布

简单点可以把高斯分布当作一个function，输入就是一个向量x ，输出就是选中 x的概率（实际上高斯分布不等于概率，只是和概率成正比，这里简单说成概率）。function由期望 μ 和协方差矩阵 Σ 决定。下图表示相同的 μ ， Σ 不同，概率分布的最高点是一样的，但是离散度是不一样的；不同的 μ ， 相同的Σ ，则概率分布的最高点的位置是不同的


假设通过79个点估测出了期望 μ 和协方差矩阵 Σ。期望是图中的黄色点，协方差矩阵是红色的范围。现在给一个不在79个点之内的新点，用刚才估测出的期望和协方差矩阵写出高斯分布的function $f_{\mu ,\Sigma }(x)$，然后把x带进去，计算出被挑选出来的概率

求解μ,Σ：Maximum Likelihood（最大似然估计）

求出${\mu }_1$,${\Sigma }_1$,${\mu }_2$,${\Sigma }_2$可以进行分类了。

更新model

如果每个类别$i$都有一个协方差矩阵Σ，一方面，variance过大，容易过拟合，另一方面，共享协方差矩阵可以减少参数个数。共用的$\Sigma =\frac{79}{140}{\Sigma }_1+\frac{61}{140}{\Sigma }_2$

右图新的结果，分类的boundary是线性的，所以也将这种分类叫做 linear model。如果考虑所有的属性，发现正确率提高到了73%

总结：

Posterior Probability

通过对后验概率的数学变形，推导出了sigmod函数。并且可以推出$z=w\cdot x+b$

逻辑回归

step1：Function Set

找到$p_{w,b}(C_1|x)$,若$p_{w,b}(C_1|x)$ ≥0.5，则输出C1，否则输出C2。
其中$p_{w,b}(C_1|x)=\sigma (z)$,$z=wx+b$,$\sigma (z)=\frac{1}{1+e^{-z}}$
因此Function Set：$f_{w,b}(x)=p_{w,b}(C_1|x)$，including all different w,b

step 2:Goodness of a Function

step 3：find the best function

为什么逻辑回归的损失函数不能用均方误差？

对于两个参数的变化，对总的损失函数作图：

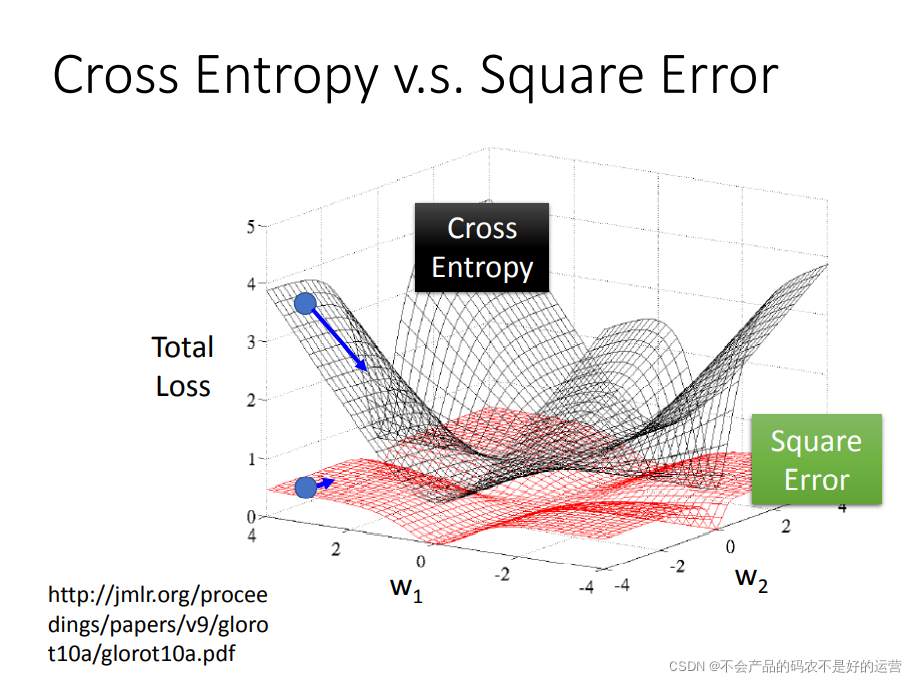
如果是交叉熵，距离target越远，微分值就越大，就可以做到距离target越远，更新参数越快。而平方误差在距离target很远的时候，微分值非常小，会造成移动的速度非常慢，这就是很差的效果了。

Discriminative（判别）v.s. Generative（生成）

逻辑回归的方法称为Discriminative（判别） 方法；上一篇中用高斯来描述后验概率，称为 Generative（生成） 方法。

如果是逻辑回归，就可以直接用梯度下降法找出w和b；如果是概率生成模型，像上篇那样求出 μ1 ， μ2 ，协方差矩阵的逆，然后就能算出w和b，用逻辑回归和概率生成模型找出来的w和b是不一样的。

上图的训练集有13组数据，类别1里面两个特征都是1，剩下的(1, 0), (0, 1), (0, 0) 都认为是类别2；然后给一个测试数据(1, 1)，它是哪个类别呢？人类来判断的话，不出意外基本都认为是类别1。朴素贝叶斯分类器（Naive Bayes）判断（1，1）属于类别1的概率<0.5，所以属于类别2。这其实是合理的，因为目前实际上训练集的数据量太小，对于 (1, 1)可能属于类别2这件事情，朴素贝叶斯分类器是有假设这种情况存在的（机器脑补这种可能性==）。所以结果和人类直观判断的结果不太一样。

判别（Discriminative）方法不一定比生成（Generative）方法好

生成方法的优势：
1、训练集数据量很小的情况；因为判别方法没有做任何假设，就是看着训练集来计算，训练集数量越来越大的时候，error会越小。而生成方法会自己脑补，受到数据量的影响比较小。
2、对于噪声数据有更好的鲁棒性（robust）。
3、先验和类相关的概率可以从不同的来源估计。比如语音识别，可能直观会认为现在的语音识别大都使用神经网络来进行处理，是判别方法，但事实上整个语音识别是 Generative 的方法，DNN只是其中的一块而已；因为还是需要算一个先验概率，就是某句话被说出来的概率，而估计某句话被说出来的概率不需要声音数据，只需要爬很多的句子，就能计算某句话出现的几率

softmax回归

如果定义类别1 y^ =1，类别2 y^ =2 ，类别3 y^ =3，这样会人为造成类别1 和类型2有比类别1和类别3离的近，可以用以下表示y

逻辑回归的限制

这里的逻辑回归所能做的分界线就是一条直线，没有办法将红蓝色用一条直线分开。

Feature Transformation

类别1转化为某个点到 (0,0) 点的距离，类别2转化为某个点到 (1,1) 点的距离。然后问题就转化右图，此时就可以处理了。但是实际中并不是总能轻易的找到好的特征转换的方法。

Cascading logistic regression models（级联逻辑回归模型）

我们想让机器自己产生这个transformation，我们把很多个逻辑回归接起来就可以做到这样的事情

如上图就是用两个逻辑回归 z1和 z2来进行特征转换，然后对于 x′1 和 x′2，再用一个逻辑回归进行分类

一个逻辑回归的输入可以来源于其他逻辑回归的输出，这个逻辑回归的输出也可以是其他逻辑回归的输入。把每个逻辑回归称为一个 Neuron（神经元），把这些神经元连接起来的网络，就叫做 Neural Network（神经网络）