1 信息熵
1.1 信息熵

事件越不确定熵越大,越确定熵越小,如果熵为0,表示这件事情一定发生,就好比你说了一句废话
1.2 条件熵
H(Y|X) = H(X,Y) - H(X),在X发生的前提下,Y发生新带来的熵
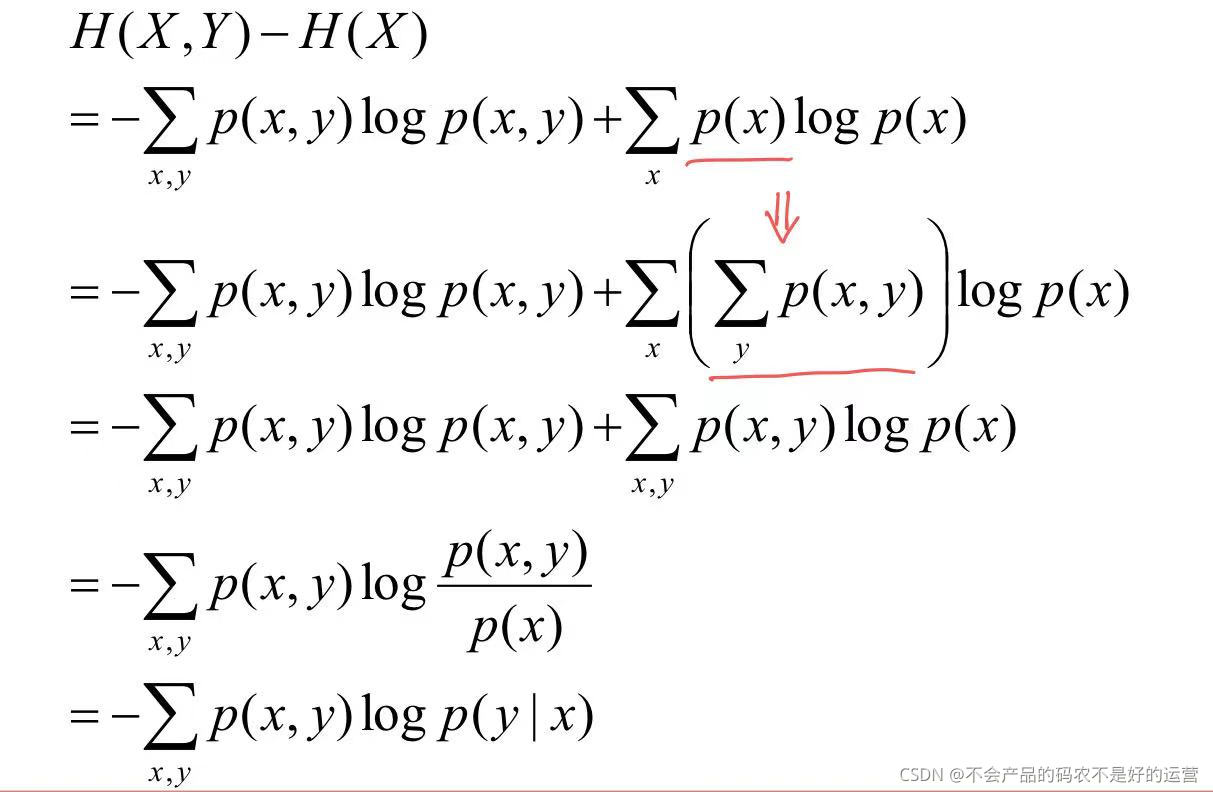
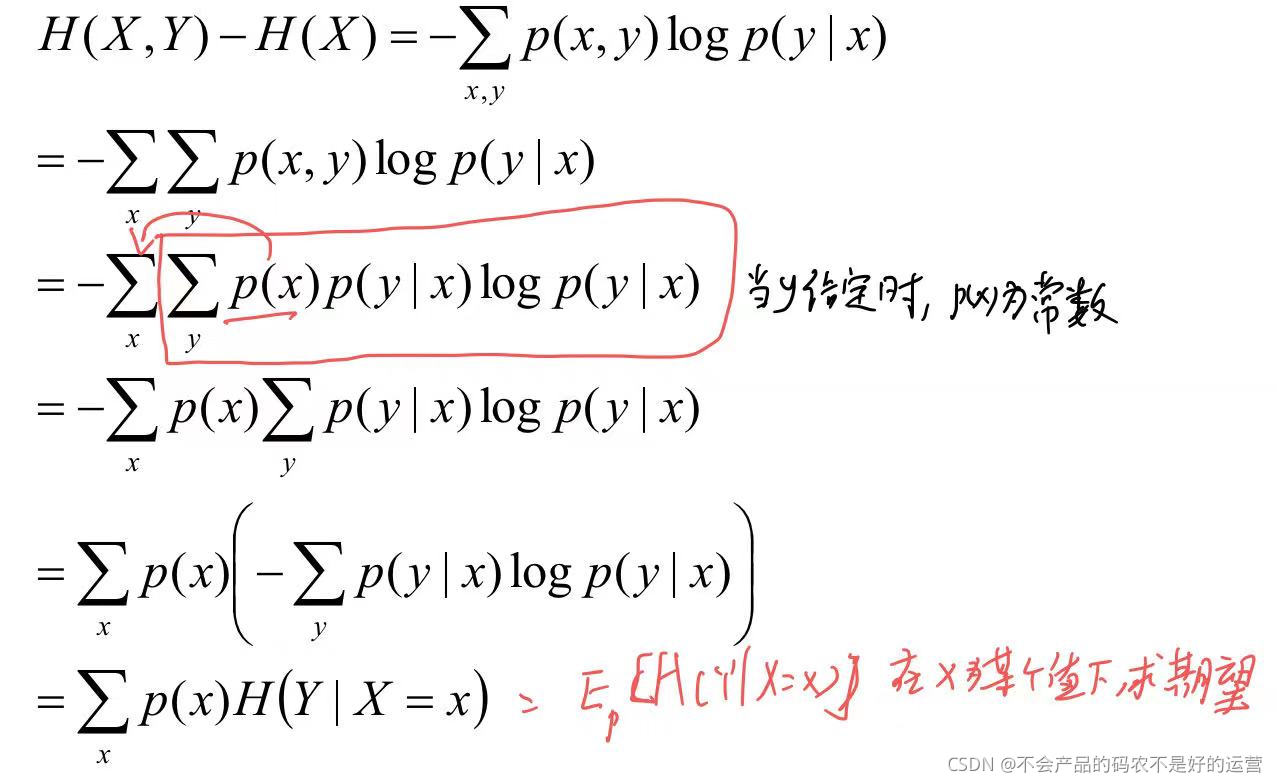
1.3 相对熵、互信息


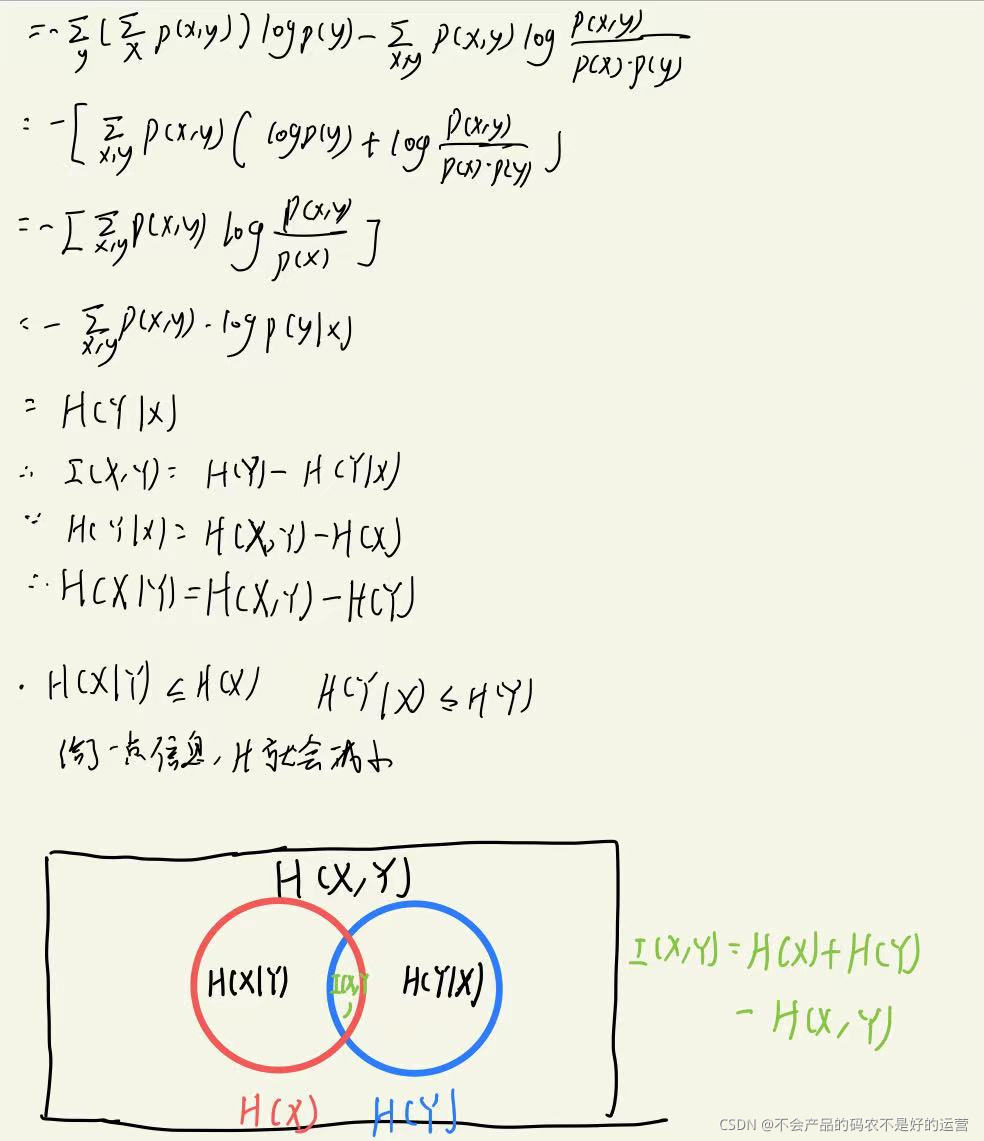
我们的目标函数可以是极大似然估计求最大值,也可以是交叉熵求最小值
2 决策树学习算法
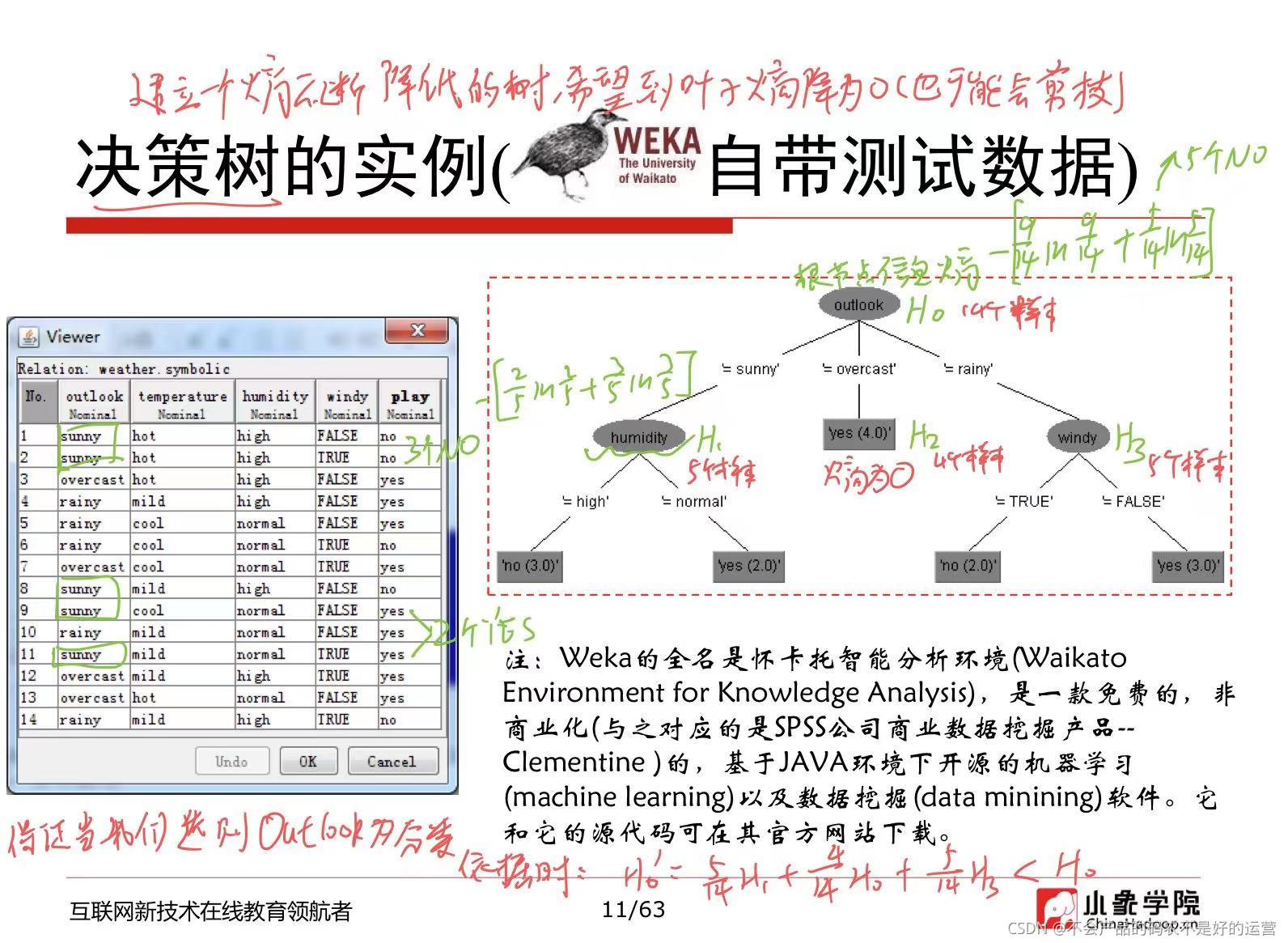
建决策树就是建立一个熵不断降低的树
2.1 三种决策树学习算法


2.2 决策树的过拟合
2.2.1、剪枝
1、预剪枝
2、后剪枝
(1)降低错误剪枝
模型的某个节点在剪枝后,如果测试集中错误的个数减少,那这个节点的分支应该剪枝,如剪枝前,误判个数为2个,剪枝后误判个数为1个,那这个枝就应该被剪掉。
这个方法受到测试集的影响较大,如果测试集比训练集小,会限制分类的精度,可能会让模型欠拟合

2.2.2、随机森林
2.3 决策树的损失函数
选出n个样本
2、在所有属性上,对这n个样本建立分类器(ID3、C4.5、CART、SVM、逻辑回归等),但一般不用SVM和逻辑回归使用Bagging策略。
重复以上两步m次,即可获得m个分类器。将数据放入这些分类器上,最后根据这m个分类器的投票结果,决定数据属于哪一类。


需要注意的是可能会有36.8%的数据没参与到建某棵树的过程,这些数据成为out of Bag,它可以用来做测试决策树分类性能的好坏
3.2 随机森林


样本不均衡问题如何处理:
样本不均衡:如共有1000个样本,990个负类,只有10个正类
解决方法:
1、降采样:α为采样率,假设是10%,则在负类中随机选择99个样本,和10个正类训练一个决策树
2、重采样:10个样本重复采样,比如10倍的重采样率,则有100个正类和990个负类来训练模型,需要注意的是,在这10个样本中,xA可能在决策树A中中重复了20次,在决策树B中可能重复了10次
3、**造数据:**两个样本点直接随机插入一个新的样本

3.2.1 使用随机森林建立样本间的相似度
如果x1和x2出现在同一叶子节点下的次数多,可以认为x1和x2相似度比较高

3.2.2 使用随机森林进行特征筛选
一个特征在多个节点出现,说明这个特征很重要

3.2.3 使用随机森林进行异常数据检测
异常值通常很快到达叶子

3.2.4 使用随机森林进行回归
依旧是用MSE作为损失函数
























 222
222

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








