一文读懂贝叶斯，不再忘记

全概率公式：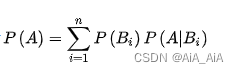

联合概率公式：

贝叶斯公式：

百度百科关于条件概率：条件概率_百度百科

下面是一个虚构但现实的例子，P(A|B) 与 P(B|A)的差距可能令人惊讶，同时也相当明显。

若想分辨某些个体是否有重大疾病，以便早期治疗，我们可能会对一大群人进行检验。虽然其益处明显可见，但同时，检验行为有一个地方引起争议，就是有检出假阳性的结果的可能：若有个未得疾病的人，却在初检时被误检为得病，他可能会感到苦恼烦闷，一直持续到更详细的检测显示他并未得病为止。而且就算在告知他其实是健康的人后，也可能因此对他的人生有负面影响。

这个问题的重要性，最适合用条件机率的观点来解释。

假设人群中有1%的人罹患此疾病，而其他人是健康的。我们随机选出任一个体，并将患病以disease、健康以well表示：

P(disease) = 1% = 0.01 and P(well) = 99% = 0.99. 假设检验动作实施在未患病的人身上时，有1%的机率其结果为假阳性（阳性以positive表示）。意即：

P(positive | well) = 1%，而且P(negative | well) = 99%. 最后，假设检验动作实施在患病的人身上时，有1%的机率其结果为假阴性（阴性以negative表示）。意即：

P(negative | disease) = 1%且P(positive | disease) = 99%。由计算可知：P(negative | well) = 99%

是整群人中健康、且测定为阴性者的比率。

P(positive|disease) = 99% 是整群人中得病、且测定为阳性者的比率。

是整群人中被测定为假阳性者的比率。

是整群人中被测定为假阴性者的比率。

进一步得出：

是整群人中被测出为阳性者的比率。

P(disease|positive) = 50% 是某人被测出为阳性时，实际上真的得了病的机率。

这个例子里面，我们很轻易可以看出 P(positive|disease)=99% 与 P(disease|positive)=50% 的差距：前者是你得了病，而被检出为阳性的条件机率；后者是你被检出为阳性，而你实际上真得了病的条件机率。由我们在本例中所选的数字，最终结果可能令人难以接受：被测定为阳性者，其中的半数实际上是假阳性。 

上述介绍的公式一直记不住，下面用一个表格，将朴素贝叶斯、联合概率、全概率，条件概率，说的都明明白白，容易记忆。

1.类似于混淆矩阵内的  C4、C5、D4、D5均为条件概率。 例如P(C4)=P(positive|well)=0.01

2.C6、D6内的为well和disease本身占总体的比例，为先验概率，事先统计出来的。即为P(Well),P(disease)

3.如何求E4、E5中的问号？这个是positive和negetive占总体的比例，
即为：P(positive),p(negetive).按照全概率公式：  E4=C6*C4+D6*D4， 这个其实就是第6行乘以第4行，其实就是加权平均。

4.如何求联合概率。联合概率其实是全概率的一部分。就是第四行和第6行，对应位置相乘。

5.条件概率本质上是：P(B|A) 事件A和事件B同时发的概率P(AB)除以 事件B的概率P(A)..

6.朴素贝叶斯，其实就是将条件概率的计算方式展开。