二叉树删除简单易行易于理解！！！！

内容理解
参考：https://blog.youkuaiyun.com/u013834525/article/details/80506126
二叉树的增删改查

其他都简单就是删除比较麻烦

分三种情况考虑
1.没有子节点的情况
2.有1个子节点
3.有两个子节点
主要就是有两个子节点情况代码步骤
a.当删除节点是 头节点的时候
============1.先用一个变量暂存遍历到头节点右边的最左边的节点
============2.将头节点的左边全部移到刚才查找的变量的左边
-===========3.再将头节点变为原来头结点的右边起始节点
b.当删除的节点不是头的话
============1.先判断是在父亲节点的左边还是右边
============2.将要删除的节点遍历到右边的最左边
============3.将要删除节点的左边全部移动到要刚刚遍历的最左边
============4.在将刚刚判断过的在父亲节点的左边还是右边将父节点和要删除节点右边起始节点相连接

删除头节点

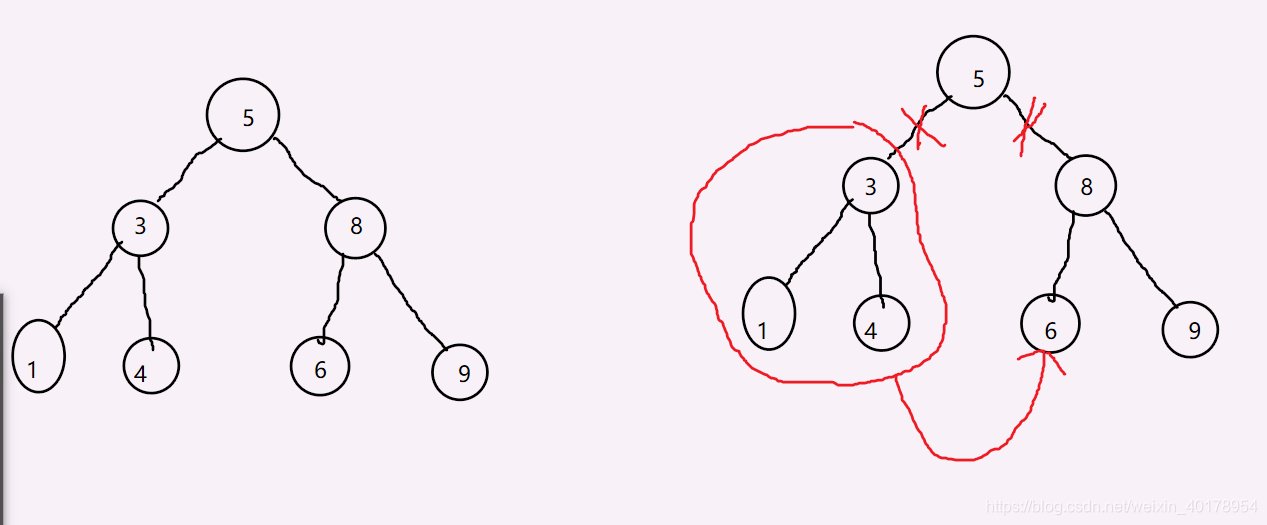
删除后

删除中间

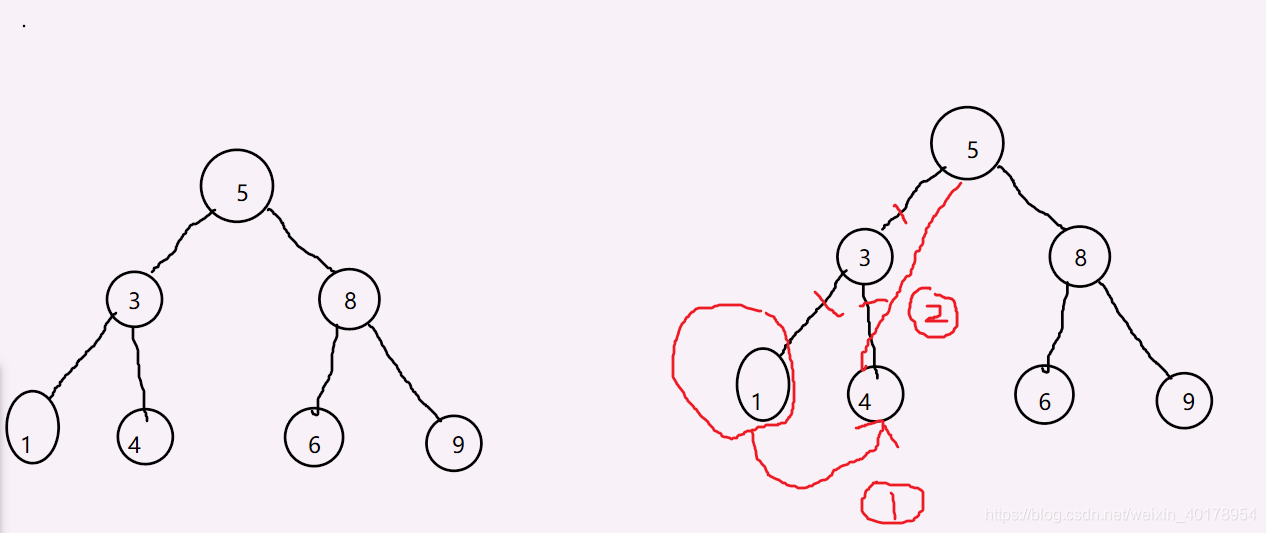
删除后

代码

#include <stdio.h>
#include <stdlib.h>


typedef struct tree{
	int data;
	struct tree *left;
	struct tree *right;
	
}Tree;


//查找节点并且同时记录节点的数值和父亲节点的数值
Tree * find_node;
Tree * parent_node;
void find_tree(Tree *root,int data){
	if(root != NULL){
		//如果找到节点则返回
		if(root->data == data){
			find_node=root;
			parent_node=NULL;
			return ;
		}else if(root->data > data){//没找到则根据大小进行便利并且同时记录上节点的父亲节点
			parent_node = root;
			find_tree(root->left,data);
		}else{
			parent_node=root ;
			find_tree(root->right,data);
		}
	}
}
//destory tree
void destory_tree(Tree *root){
	if(root){
		destory_tree(root->left);
		destory_tree(root->right);
		free(root);
	}
}
//删除节点
void delete_tree(Tree **root,int data){
	Tree *temp_node;
	//找到要删除的节点以及父亲节点 
	find_tree(*root,data);
	//分三种种情况讨论
	//第一种情况也是最简单就是不存在子节点的节点删除
	if(find_node->left==NULL&&find_node->right==NULL){
		if(parent_node->left==find_node)
			parent_node->left = NULL;
		else
			parent_node->right = NULL;
		//进行2
		free(find_node);
		return ;
	}
	//第二种情况也就是中间节点，存在两边都是节点的情况
	else if(find_node->right!=NULL&&find_node->right!=NULL){

		//删除头节点
		if(find_node == *root){
			printf("the node is head\n");
			temp_node = (*root)->right;
			//便利到最左边
			while(temp_node->left!=NULL){
				temp_node=temp_node->left;
			}
			temp_node->left = (*root)->left;
			*root=(*root)->right;
			free(find_node);
			return;
		}
		else{
			//将这个节点插入到当前要删除节点右边的最左边
			Tree *temp_node2 = find_node;
			temp_node2=temp_node2->right;
			while(temp_node2->left=NULL){
				temp_node2=temp_node2->left;
			}
			temp_node2->left = find_node->left;
			if(parent_node->left == find_node)
				parent_node->left = find_node->right;
			else
				parent_node->right = find_node->right;
			free(find_node);
			return ;
		}
	}else{
		if(parent_node->left=find_node){
			if(find_node->left!=NULL)
				parent_node->left = find_node->left;
			else
				parent_node->left = find_node->right;
		}else{
			if(find_node->left!=NULL)
				parent_node->right = find_node->left;
			else
				parent_node->right = find_node->right;
		}
		free(find_node);
		return ;
	}
}


//前面 bianli
void pre_order(Tree *node){
	if(node == NULL)
		return ;
	printf("%d\n", node->data);
	pre_order(node->left);
	pre_order(node->right);
}
void middle_order(Tree *node){
	if(node == NULL)
		return ;
	pre_order(node->left);
	printf("%d\n", node->data);
	pre_order(node->right);
}
void back_order(Tree *node){
	if(node == NULL)
		return ;
	pre_order(node->left);
	pre_order(node->right);
	printf("%d\n", node->data);
}
//初始化节嗲
struct tree *init_tree(int data ){
	Tree *newnode;
	newnode=(Tree *)malloc(sizeof(Tree));
	newnode->data=data;
	newnode->left=NULL;
	newnode->right=NULL;
	return newnode;
}
//插入节点
void inser_tree(Tree **root,Tree * newnode)
{
	if(*root == NULL)
		*root = newnode;
	else if(newnode->data > (*root)-> data)
		inser_tree(&((*root)->right),newnode);
		else
			inser_tree(&((*root)->left),newnode);
}

int main(int argc, char const *argv[])
{
	Tree *root=NULL;
 	Tree *newnode=NULL;
    int data;
    int a[7]={5,3,1,4,8,6,9};
    int i;
    for(i=0;i<7;i++){
    	newnode=init_tree(a[i]);
    	inser_tree(&root,newnode);
  	}
  	data = 3;
  	delete_tree(&root,data);
  	pre_order(root);
  	
  	//find_tree(root,data);
  	//printf("child Tree_node is:%d parent_node is %d\n",find_node->data,parent_node->data);
	return 0;
}