算法-基础-排序算法

程序员不二

已于 2022-04-19 17:36:40 修改

阅读量912

点赞数

分类专栏：算法文章标签： java 算法 leetcode

于 2022-04-17 23:02:19 首次发布

本文链接：https://blog.youkuaiyun.com/weixin_40113390/article/details/124220681

版权

算法专栏收录该内容

40 篇文章

订阅专栏

本文详细介绍了八大排序算法：选择排序、冒泡排序、快速排序、插入排序、Shell排序、归并排序、基数排序和堆排序。内容包括每种排序算法的时间复杂度、基本思想及优化策略，帮助读者理解各种排序算法的原理和应用场景。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

文章目录

八大排序算法

八大排序算法

排序算法时间复杂度

排序算法

1, 选择排序(最容易想到)

时间复杂度: O(n²)
最好的情况下也是：O(n²)

大体思路：
第一轮从数组中选取最大的数据，放在最后一位。
第二轮从除了倒数第一位之外剩余的那些数中选择最大的，放在倒数第二位
第三轮从除了倒数后两位之外剩余的那些数中选取最大的，放在倒数第三位
…
n个数字经过(n-1)轮后，即可保证有序

package com.shangguigu.dachang.algrithm.A08_sort;

import java.util.Arrays;

/**
 * @author : 不二
 * @date : 2022/4/17-上午12:46
 * @desc : 选择排序
 **/
public class A03_SelectSort {
    public static void main(String[] args) {
        int[] nums = {9, -2, -1, 3, 10, 100, -3, 3, 4, 20};
        selectSort(nums);
        System.out.println(Arrays.toString(nums));
    }

    private static void selectSort(int[] nums) {
        for (int i = 0; i < nums.length; i++) {
            int maxIndex = 0;
            for (int j = 1; j < nums.length - i; j++) {
                if (nums[maxIndex] < nums[j]) {
                    maxIndex = j;
                }
            }
            // 然后把最大的数据和对应的位置交换
            if (maxIndex != (nums.length - i - 1)) {
                int temp = nums[nums.length - i - 1];
                nums[nums.length - i - 1] = nums[maxIndex];
                nums[maxIndex] = temp;
            }
        }
    }
}

2, 冒泡排序算法

时间复杂度： O(n²)

相邻的两个进行比较，如果前者比后者大，那么就把大的移动到后面。
第一轮把最大的移动到最后一位
第二位把次大的移动到倒数第二位
依次进行，直到有序(n个数最大进行n-1轮即可有序)

package com.shangguigu.dachang.algrithm.A08_sort;

import java.util.Arrays;

/**
 * @author : 不二
 * @date : 2022/4/16-下午9:26
 * @desc : 冒泡排序
 **/
public class A01_BubbuleSort {
    public static void main(String[] args) {
        int[] nums = {9, -2, -1, 3, 10, 100, -3, 3, 4, 20};
        bubbleSort(nums);
        System.out.println(Arrays.toString(nums));
    }

    /**
     * 每次遍历， 把最大的通过冒泡的方式移动到顶端
     * 然后下一次遍历，把剩余最大的通过冒泡的方式移动到剩余数据的顶端
     */
    public static void bubbleSort(int[] arr) {
        for (int i = 0; i < arr.length; i++) {
            // 这里要多减去1
            for (int j = 0; j < arr.length - i -1; j++) {
                if (arr[j] > arr[j + 1]) {
                    int tmp = arr[j];
                    arr[j] = arr[j + 1];
                    arr[j + 1] = tmp;
                }
            }
        }
    }
}

3, 快速排序(常用)(平分移动+迭代排序)-冒泡算法的优化

时间复杂度： O(n $log_2 n$ )

快速排序思路
首先以中间一个数字为基准，把该数右侧大于该数的移至该数左侧，把该数左侧大于数的移至该数右侧。这样大于该数的数字都在右侧，小于该数的都在该数左侧。
接着再使用迭代算法, 依次对左侧的进行相同方法的移动。
接着再使用迭代算法, 依次对右侧的进行相同方法的移动。
当迭代结束，该数组数字即是有序

思路1: 中间值作为pivot，左右双指针移动

package com.shangguigu.dachang.algrithm.A08_sort;

import java.util.Arrays;

/**
 * @author : 不二
 * @date : 2022/4/16-下午9:43
 * @desc : 快速排序
 **/
public class A02_QuickSort_mid_pivot {
    public static void main(String[] args) {
        int[] nums = {9, -2, -1, 3, 10, 100, -3, 3, 4, 20};
        quickSort(nums, 0, nums.length - 1);
        System.out.println(Arrays.toString(nums));
    }

    /**
     * 思路1：以中间为界限，通过左右双指针，把大于中间界限的数据移动到右侧，小于中间界限的数据移动到左侧
     * 然后左侧部分数据和右侧部分数据分别迭代调用上述规则
     * 这里用的左右指针
     */
    private static void quickSort(int[] nums, int left, int right) {
        if (left < right) {
            int midIndex = (left + right) / 2;
            int midValue = nums[midIndex];

            // 这里定义两个指针，后续指针会根据数据的情况进行移动
            // left和right左右两个参数不能更改.
            int leftPointer = left, rightPointer = right;
            while (leftPointer < rightPointer) {
                // 左指针向右移动，直到找到大于中间值的数据
                while (nums[leftPointer] < midValue) {
                    leftPointer++;
                }
                // 右指针向左移动，直到找到小于中间值的数据
                while (nums[rightPointer] > midValue) {
                    rightPointer--;
                }

                int temp = nums[leftPointer];
                nums[leftPointer] = nums[rightPointer];
                nums[rightPointer] = temp;

                // 因为和中间值相同的数据，所以如果左右两个指针的数据和中间值相同，那么必须得有一个指针跳出来
                if (nums[leftPointer] == midValue && nums[rightPointer] == midValue) {
                    leftPointer++;
                }
            }

            // 这个时候leftPointer == rightPointer
            // 而且需要作为新的中间值进行迭代调用
            quickSort(nums, left, rightPointer - 1);
            quickSort(nums, leftPointer, right);
        }
    }
}

思路2: 最左或者最右数据作为pivot

这里尝试使用其他方式解决

package com.shangguigu.dachang.algrithm.A08_sort;

import java.util.Arrays;

/**
 * @author : 不二
 * @date : 2022/4/17-上午12:28
 * @desc : 快速排序
 **/
public class A02_QuickSort_start_pivot {

    public static void main(String[] args) {
        int[] nums = {9, -2, -1, 3, 10, 100, -3, 3, 4, 20};
        // quickSort(nums, 0, nums.length - 1);
        quickSort_v2(nums, 0, nums.length - 1);
        System.out.println(Arrays.toString(nums));
    }

    /**
     * 思路2：这里也尝试使用一下快慢指针(这里其实是双循环)
     */
    private static void quickSort_v2(int[] arr, int left, int right) {
        // 这个是必须的，left肯定小于right
        if (left < right) {
            // 1, 设定基准值（pivot）
            // 这里基准值设备最左侧数据
            int pivot = left;
            int index = pivot + 1;
            for (int i = index; i <= right; i++) {
                // 这里i和pivot相同的话，这里也是要交换的，感觉有点多余
                if (arr[i] < arr[pivot]) {
                    // 不相等的时候才交换
                    if (i != pivot) {
                        int tmp = arr[i];
                        arr[i] = arr[index];
                        arr[index] = tmp;
                    }
                    index++;
                }
            }

            // 然后确定中间位置，方便后续根据中间位置继续处理
            int temp = arr[pivot];
            arr[index-1] = arr[pivot];
            arr[pivot] = temp;
            
            int partitionIndex = index - 1;
            quickSort(arr, left, partitionIndex - 1);
            quickSort(arr, partitionIndex + 1, right);
        }
    }


    /**
     * 思路2：以最左侧数据作为pivot
     * 把小于pivot的数据移动到pivot左侧，大于pivot的数据移动到pivot右侧
     * 这里用的是左右指针
     */
    private static void quickSort(int[] nums, int left, int right){
        if (left < right) {
            int midIndex = left;
            int midValue = nums[midIndex];

            // 这里定义两个指针，后续指针会根据数据的情况进行移动
            // left和right左右两个参数不能更改.
            int leftPointer = left, rightPointer = right;
            while (leftPointer < rightPointer) {
                // 左指针向右移动，直到找到大于中间值的数据
                while (nums[leftPointer] < midValue) {
                    leftPointer++;
                }
                // 右指针向左移动，直到找到小于中间值的数据
                while (nums[rightPointer] > midValue) {
                    rightPointer--;
                }

                int temp = nums[leftPointer];
                nums[leftPointer] = nums[rightPointer];
                nums[rightPointer] = temp;

                // 因为和中间值相同的数据，所以如果左右两个指针的数据和中间值相同，那么必须得有一个指针跳出来
                if (nums[leftPointer] == midValue && nums[rightPointer] == midValue) {
                    leftPointer++;
                }
            }

            // 这个时候leftPointer == rightPointer
            // 而且需要作为新的中间值进行迭代调用
            quickSort(nums, left, rightPointer - 1);
            quickSort(nums, leftPointer, right);
        }
    }
}

4, 插入排序

时间复杂度：O(n²)
在最好的情况下：时间复杂度为：O(n), 比选择排序要好

1，第一轮把第二个数和第一个比较，如果比第一个小，那么把第一个后移一位，然后把第二个数赋值到第一位上
2，第二轮把第三个数和第二个数比较，如果比第二个小，那么把第二个数后移一位，然后再和第一个数比较，如果还比第一个数小(否则把第三个数赋值到第二位上)，再把第一个数后移一位，把第三个数赋值到第一位上。
3，依次执行如上逻辑
4，n个数字经过(n-1)轮插入，即可保证有序
简单来讲就是：
先第二个和第一个比较
然后第三个和前两个比较
然后第四个和前三个比较
…
最后第n个前前n-1个比较

注意：插入是先在前面的数据中找到应该插入的位置，最后才会插入
这个和冒泡有点类似，不过冒泡是先替换，然后再冒泡。插入时先找到最后位置，最后再替换。
插入的重点是: 把后面的一次往后移动一位，空出需要插入的，然后插入即可

package com.shangguigu.dachang.algrithm.A08_sort;

import java.util.Arrays;

/**
 * @author : 不二
 * @date : 2022/4/17-上午12:58
 * @desc : 插入排序
 **/
public class A04_InsertSort {
    public static void main(String[] args) {
        int[] nums = {9, -2, -1, 3, 10, 100, -3, 3, 4, 20};
        insertSort(nums);
        System.out.println(Arrays.toString(nums));
    }

    private static void insertSort(int[] nums) {
        for (int i = 1; i < nums.length; i++) {
            //即将被插入的数字和索引记录下来
            int lstOne = nums[i];
            // int lstOneIndex = i;

            int thePos = i - 1;
            // 要保证thePos最小为0，如果0也比lstOne大，那么thePos最后会减去到-1
            while (thePos >= 0 && nums[thePos] > lstOne) {
                // 如果进来，说明thePos数据比lstOne大，把lstOne位置数据后移一位。
                nums[thePos + 1] = nums[thePos];
                thePos--;
            }

            // 走到这里的话，说明thePos必然比lstOne小了，那么lstOne需要插入到thePos+1的位置了
            nums[thePos + 1] = lstOne;
            System.out.println("----");
        }

    }
}

5, shell排序(插入排序优化)

shell排序是插入排序的优化，以减少数据插入之前为了找到插入位置而可能后移次数过多的问题
shell排序的时候有两种方式：
1，交换法。直接进行交换，速度慢
2，移动法，先移动，而不是直接交换。速度快,超级快！80万只需要20ms左右。

第一种shell排序：直接交换

package com.shangguigu.dachang.algrithm.A08_sort;

import java.util.Arrays;

/**
 * @author : 不二
 * @date : 2022/4/17-下午8:08
 * @desc :  希尔排序
 **/
public class A05_ShellSort_exchange {
    public static void main(String[] args) {
        int[] nums = {9, -2, -1, 3, 10, 100, -3, 3, 4, 20};
        shellSort(nums);
        System.out.println(Arrays.toString(nums));
    }

    private static void shellSort(int[] nums) {
        for (int gap = nums.length / 2; gap > 0; gap /= 2) {
            System.out.println(gap);
            for (int i = gap; i < nums.length; i++) {
                System.out.println("");

                // 这么遍历的话，那么直接比较当前数据和前一个数据
                // 这里类似冒泡
                for (int j = i; j >= gap; j -= gap) {
                    System.out.println("gap是：" + gap + ", i是：" + i + ", j是：" + j);
                    if (nums[j-gap] > nums[j]) {
                        int temp = nums[j-gap];
                        nums[j-gap] = nums[j];
                        nums[j] = temp;
                    }
                }
            }
            System.out.println("---");
        }
    }
}

第二种shell排序：移动，最后交换(按理来说，这个才是正宗的shell排序)

package com.shangguigu.dachang.algrithm.A08_sort;

import java.util.Arrays;

/**
 * @author : 不二
 * @date : 2022/4/17-下午8:08
 * @desc :  希尔排序
 **/
public class A05_ShellSort_move {
    public static void main(String[] args) {
        int[] nums = {9, -2, -1, 3, 10, 100, -3, 3, 4, 20};
        shellSort(nums);
        System.out.println(Arrays.toString(nums));
    }

    private static void shellSort(int[] nums) {
        for (int gap = nums.length / 2; gap > 0; gap /= 2) {
            System.out.println(gap);
            for (int i = gap; i < nums.length; i++) {
                System.out.println("");

                // 这里进行插入，先移动，最后才插入的哈
                int insertValue = nums[i];
                int thePos = i - gap;
                while (thePos >= 0 && nums[thePos] > insertValue) {
                    nums[thePos + gap] = nums[thePos];
                    thePos -= gap;
                }
                nums[thePos + gap] = insertValue;

                /*for (int j = i; j >= 0; j -= gap) {
                    System.out.println("gap是：" + gap + ", i是：" + i + ", j是：" + j);
                }*/
            }
            System.out.println("---");
        }
    }
}

6, 归并排序

时间复杂度: O(n $log_2 n$ )

归并排序算法，这个是分治算法其中一种
分完之后，通过双指针把有序数据移动到新的临时数组中，然后排好序再把这部分数据拷贝回原数组
参考：https://www.cnblogs.com/chengxiao/p/6194356.html

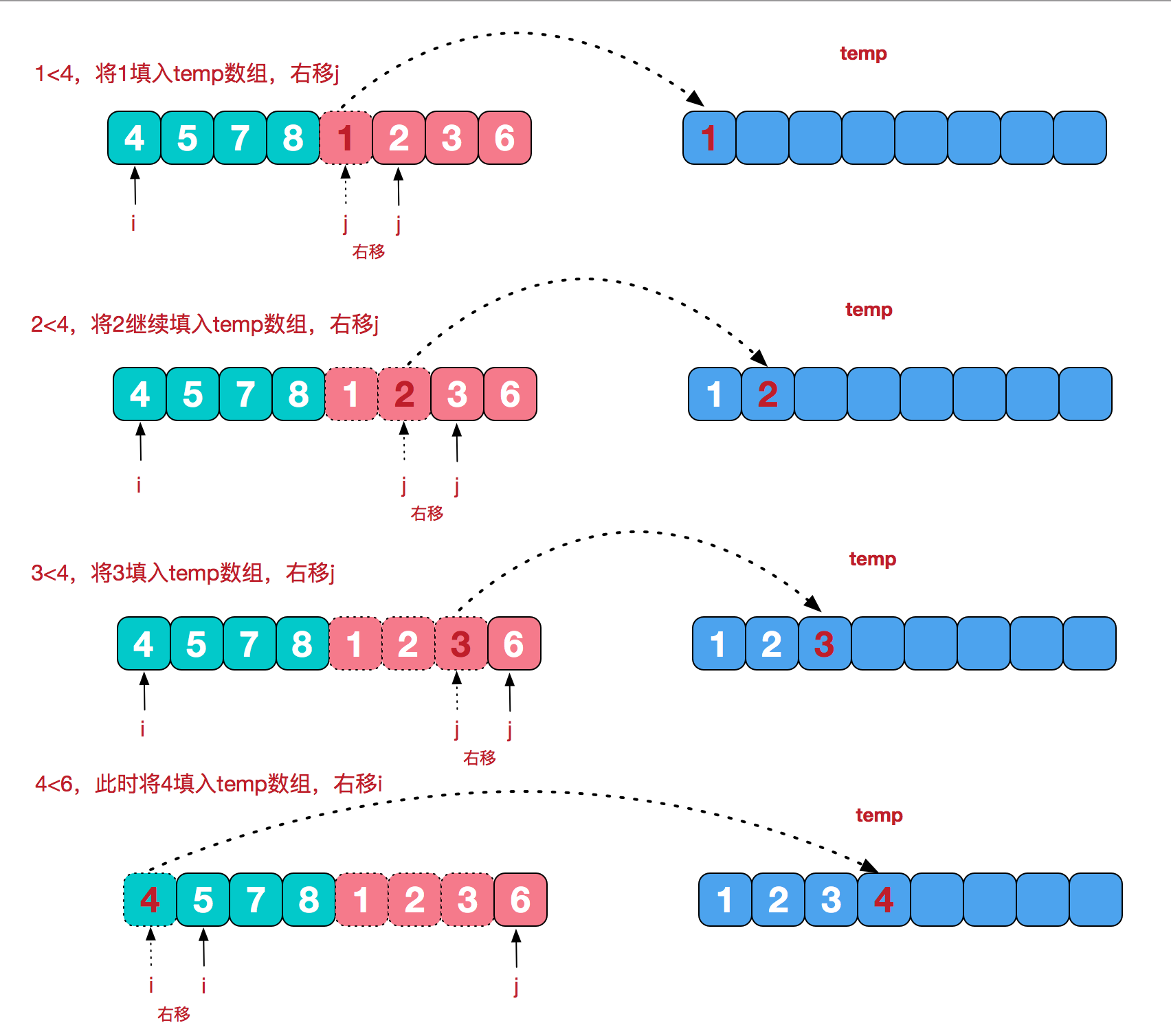
在这里插入图片描述

package com.shangguigu.dachang.algrithm.A08_sort;

import java.util.Arrays;

/**
 * @author : 不二
 * @date : 2022/4/17-下午9:15
 * @desc : 归并排序
 *
 **/
public class A06_MergeSort {
    public static void main(String[] args) {
        int[] nums = {9, -2, -1, 3, 10, 100, -3, 3, 4, 20};
        int[] tempArr = new int[nums.length];
        mergeSort(nums, 0, nums.length-1, tempArr);
        System.out.println(Arrays.toString(nums));
    }

    private static void mergeSort(int[] nums, int left, int right, int[] tempArr) {
        if (left < right) {
            int mid = (left + right) / 2;

            // 先迭代分左边
            mergeSort(nums, left, mid, tempArr);

            // 再迭代分右边
            mergeSort(nums, mid + 1, right, tempArr);

            // 分完开始从最后分的开始治理
            merge(nums, left, right, tempArr);
        }
    }

    private static void merge(int[] nums, int left, int right, int[] tempArr) {
        int mid = (left + right) / 2;

        int leftPointer = left;
        int rightPointer = (mid + 1);
        int tempArrPointer = 0;

        // 1.1, 先把合的数据按照大小顺序写入到临时数据中
        // 这里都需要是<=, 因为右边是需要包含的
        while (leftPointer <= mid && rightPointer <= right) {
            if (nums[leftPointer] < nums[rightPointer]) {
                tempArr[tempArrPointer++] = nums[leftPointer];
                leftPointer++;
            } else if (nums[leftPointer] >= nums[rightPointer]) {
                tempArr[tempArrPointer++] = nums[rightPointer];
                rightPointer++;
            }
        }
        // 1.2, 上面1.1走完，说明leftPointer到头了，或者rightPointer到头了，可能还有数据剩下，如果有剩下，一并写入到tempArr中
        // 说明左侧还有剩余
        while (leftPointer <= mid) {
            tempArr[tempArrPointer++] = nums[leftPointer];
            leftPointer++;
        }
        while (rightPointer <= right) {
            tempArr[tempArrPointer++] = nums[rightPointer];
            rightPointer++;
        }

        // 再从临时数据中取出来放回到left-right之间的位置上
        for (int i = left; i <= right; i++) {
            nums[i] = tempArr[i - left];
        }
    }
}

7, 基数排序(不考虑负数)

这里不是桶排序，桶排序是要做hash，分到不同的桶中再做排序
这个时间复杂度是非常稳定的, O(n*k)

基数排序思想：

第一轮：根据个位数字放进0-9不同的桶中

第二轮：在第一轮的顺序下，根据十位数放进0-9不同的桶中

第三轮：在第二轮的顺序下，根据百位数放进不同的桶中

…

直到最后一轮根据最大一位上的数字进行完毕，则序列即可保证有序

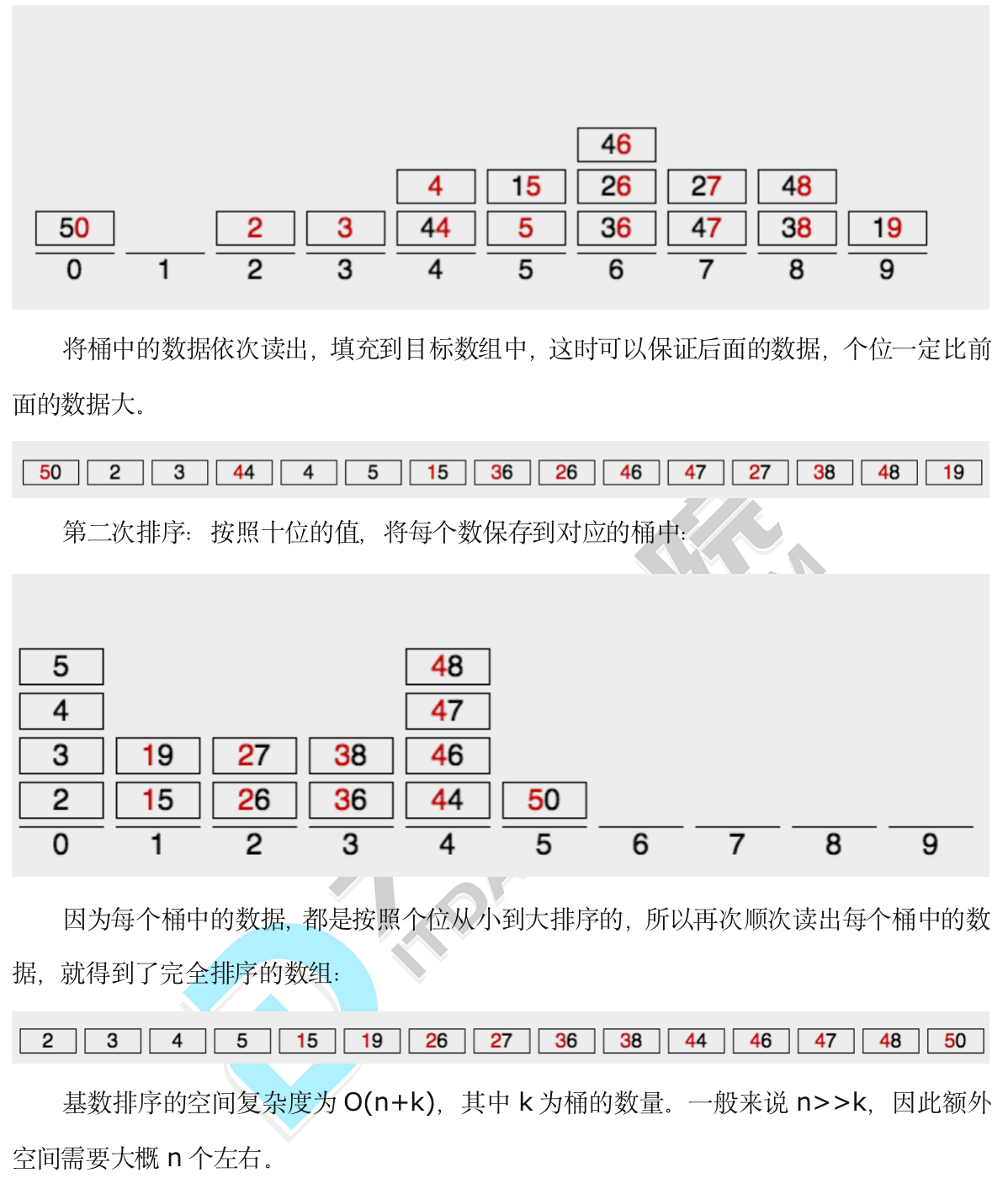
在这里插入图片描述

package com.shangguigu.dachang.algrithm.A08_sort;

import java.util.Arrays;

/**
 * @author : 不二
 * @date : 2022/4/17-下午9:46
 * @desc : 基数排序(桶排序--不考虑负数情况)
 *
 * 基数排序：0-9个不同的桶，然后分别按照个位，十位，百位数，。。。等等你放进不同的桶中，具体看代码
 * 基数排序需要10倍额外空间，所以是空间换时间的经典案例
 **/
public class A07_RadixSort {
    public static void main(String[] args) {
        // int[] nums = {9, 10, 100, 3, 4, 20};
        int[] nums = {3, -1};
        radixSort(nums);
        System.out.println(Arrays.toString(nums));
    }

    private static void radixSort(int[] nums) {
        // 第一步找到最大值
        int max = nums[0];
        for (int i = 1; i < nums.length; i++) {
            max = Math.max(max, nums[i]);
        }
        int length = (max + "").length();

        // 第二步创建需要的存储
        int[][] bucket = new int[10][nums.length];
        // 这个记录每个桶(0,1,2,3,4,5,6,7,8,9)的位置
        int[] positions = new int[10];

        // 这里有点妙
        for (int i = 0, multi = 1; i < length; i++, multi *= 10) {

            // 第一轮， 根据每个元素的个位元素进行排序
            for (int j = 0; j < nums.length; j++) {
                int current = nums[j] / multi % 10;
                System.out.println("i:" + i + ", 数据是："+ nums[j] + ",当前位数：" + current);
                bucket[current][positions[current]++] = nums[j];
            }

            // 桶中的数据取出来更新到数组里面去，方便后续从数组中进行十位处理
            int index = 0;
            for (int j = 0; j < 10; j++) {
                for (int k = 0; k < positions[j]; k++) {
                    int theData = bucket[j][k];
                    nums[index] = theData;
                    index++;
                }
            }
            positions = new int[10];
            System.out.println("-----");
        }
    }
}

8, 堆排序(大顶堆)

时间复杂度：O(n $log_2 n$ )
java优先队列PriorityQueue其实就是一个顶堆的实现

堆排序是利用堆这种数据结构而设计的一种排序算法，堆排序是一种选择排序，它最好，最坏以及平均复杂度均为O(nlogn)，它是不稳定的排序
堆是具有以下性质的完全二叉树：

大顶堆：每个节点的值大于或者等于其左右孩子节点的值(变成顺序存储二叉树的时候，数组是从大到小的)
小顶堆：每个节点的值都小于或等于其左右孩子节点的值(变成顺序存储二叉树的时候，数组是从小到大的)

package com.shangguigu.dachang.algrithm.A08_sort;

import java.util.Arrays;

/**
 * @author : 不二
 * @date : 2022/4/19-下午3:42
 * @desc : 堆排序(通过二叉树构建大顶堆)
 * 堆排序代码编写：构建大顶堆或者小顶堆
 **/
public class A08_HeapSort {
    public static void main(String[] args) {
         int[] nums = {9, 10, 100, 3, 4, 20};
//        int[] nums = {3, -1};
        heapSort(nums);
        System.out.println(Arrays.toString(nums));
    }

    private static void heapSort(int[] nums) {

        //  这里需要先构建成大顶堆方便进行后续处理
        // 首次构建大顶堆，需要从最右下，先同级往左， 然后再往上进行构建
        // 这里i要大于等于0， 因为最上级根节点也需要调整
        // arr.length / 2 - 1 是最下面的第一个非叶子节点
        for (int i = nums.length / 2 - 1; i >= 0; i--) {
            // 这里的作用是：把最大值移动到节点i处。i是从最后最左的一个非叶子开始遍历到最上面到，所以最后遍历结束之后就会变成大顶堆
            adjustHeap(nums, i, nums.length);
        }

        // 构建成大顶堆之后，最大值就是0位置的数据了，把最大值移动到末尾
        // 再根据adjustHeap把这个最小值移动到底层即可
        int temp;
        for (int i = nums.length - 1; i > 0; i--) {
            temp = nums[i];
            nums[i] = nums[0];
            nums[0] = temp;

            adjustHeap(nums, 0, i);
        }
    }

    /**
     *
     * @param arr: 给定数组
     * @param i：i是节点，这里调整i及i以下的节点，
     * @param length
     */
    public static void adjustHeap(int[] arr, int i, int length) {

        // 先把i位置也就是当前调整的根节点数据记录下来
        int temp = arr[i];

        // i位置的两个子节点分别是：2i+1，2i+2
        for (int j = 2 * i + 1; j < length; j = 2 * j + 1) {

            // 其实就是找根当前节点有关系的下层节点，一层一层遍历下去
            if (j + 1 < length && arr[j + 1] > arr[j]) {
                // 两个子节点，哪个节点的数据大，就接着从大节点往下层找
                j = j + 1;
            }

            // 如果下层已经不大于上层了，就可以退出了。
            // (这里其实都是在：先构建成大顶堆后才发挥作用的，如果我这里i是根部，但是本身数据不是大顶堆，这里是没啥用的哈)
            if (arr[j] < temp) {
                break;
            } else{
                // 说明下层有比上层大的数据
                arr[i] = arr[j];
                // 这个是下次交换就交换本次这里的这个位置的数据，而非最原始的i了
                i = j;
            }

            // 找一层换一层哈
            // 如果走完之后， 说明当前i处就是把最小值放置的位置
            arr[i] = temp;
            // 至此，最大值依次往上走， 最小值被挪至最后一行(最后一级)
        }
    }
}