Python知道cos值求角度_机械臂正运动学-DH参数-Python快速实现

# 机械臂正运动学-DH参数-Python快速实现 @[toc]

前言：

最近在玩一个非常弱智的机械臂，好多功能都没有，连个配套的仿真环境都没， 虚拟边界和碰撞检测的功能都非常难用。 没办法，我只能自己实现一个简陋的虚拟边界功能，这必须要在已知关节角的情况下，提前计算出每个关节的三维坐标。 这里的问题凝结为输入输出就是： 已知： 机械臂的关节长度，关节构型

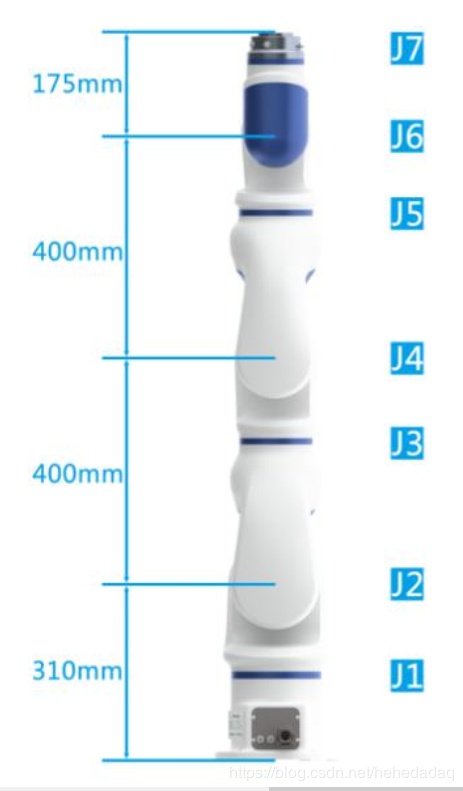
输入： 机械臂的关节角度； 输出： 机械臂的关节坐标。 全网好像没有搜到一个简单可用、基于DH参数的Python的正运动学代码（github有一个不能用）。 为了防止以后忘记，以及方便大家学习借鉴。先抛出来，供大家参考

整体思路流程：

搜集机械臂相关配置资料：关节长度、构型、官方设定的坐标系； 通过两个对应关系，找到机械臂的DH参数表； 找到了之后，代入转换矩阵T中； 连乘所有关节的T； 获取关节三维坐标。

学习资料

要想得到上面的输出，需要的基础知识比较多。 有： 1. 刚体的坐标变换； 2. DH参数； 3. 基本上就是上面两个了。

为了弄明白这个过程， 我请教了几位大佬，大佬说可以看看b站台大的机器人学，和《机器人学导论》-斯坦福的那本，自己去网上搜PDF版就好了 然后直接基本概念，大家可以去看看： 台大机器人学之运动学——林沛群（含课件+书籍）

核心概念：

我们将机械臂的每一个关节轴，都建立一个坐标系，那么从关节1到关节0的变化，其实就是做了一次刚体的坐标变换。 而关节7的末端点，则是串着做了好多次的坐标变换。

DH参数的理解。

先挂一个参考链接，这里面的介绍的更详细： https://blog.youkuaiyun.com/aic1999/article/details/82490615 上节说到本质是坐标变换，那么我们如何根据已知信息，确定好坐标变换的基本信息？ 这里面就得用到一个神奇的DH参数（两位大佬名字的缩写） 来看看课本里的这张经典图。

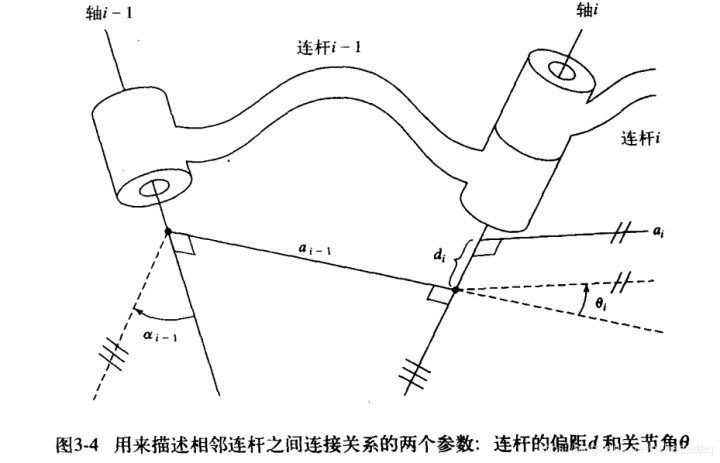
我们需要知道，决定四个轴的相对位置关系，我们可以用四个变量来描述（虽然可能不唯一，但是够了）。 那么我们需要知道的第一个对应关系：

DH参数的定义：

沿着轴方向，逆时针为正。

这里面我们还差一个东西，如何定义坐标系？

建立坐标系

其实一般如果是靠谱的机器人，这个坐标系应该是给的。

把我这次用的机器人的拿过来，作为例子，有例子，大家理解起来就方便了。

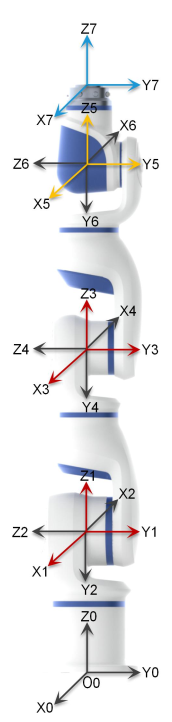
可以看出来一个很有意思的事情， 01关节是放在一起看了，即12坐标系原点重合，这里是将1杆的长度看作0了。下面去计算DH参数的时候也需要注意的。而且我们计算的时候，是无法计算出1轴的坐标。

坐标系和参数对应关系来了，我们就能填好DH表了： 如何填写？ 对着坐标轴的图和连杆参数定义，一个一个填。

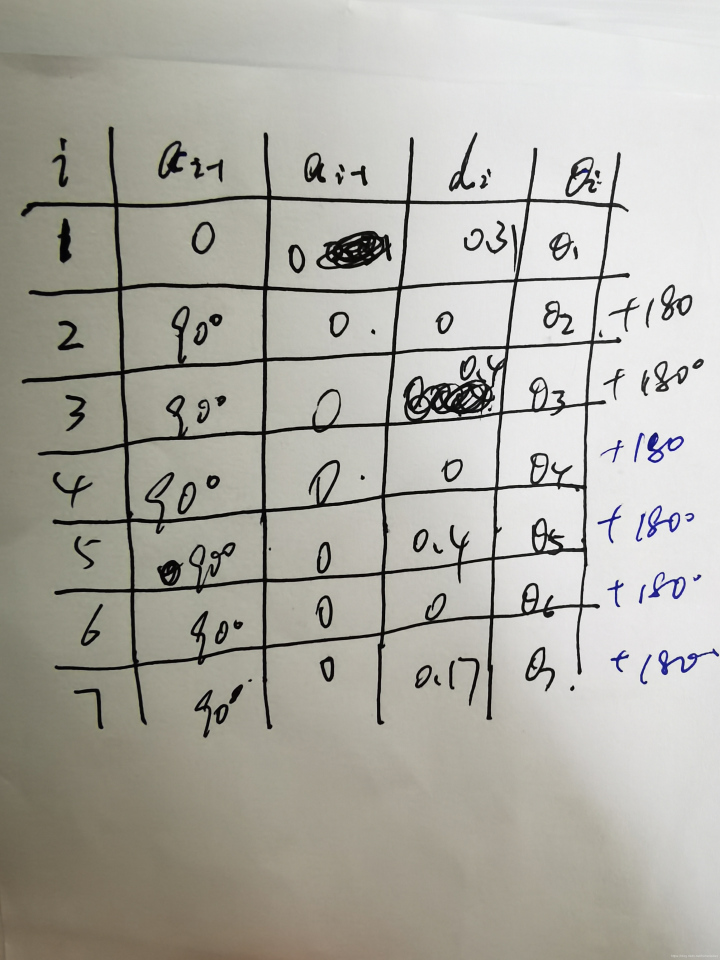
我们以第一个轴为例，第一行有四个值：$alpha$~1-0~ , $a$~1-0~ , $d$~1-0~ $theta$~1-0~ 这里面的$alpha$~1-0~即$alpha$~0~是绕X~0~正方向, 从Z~0~旋转到Z~1~的角度。从图中可以看出来，没旋转，即为0. $a$~0~沿着X~0~,从Z~0~移动到Z~1~的距离，因为两个Z重合，不存在移动距离，即距离为0； d~1~的话，不一样，沿着Z~1~轴，从X~0~移动到X~1~的距离，可以看出来，移动了0.31米，虽然方向不一样，但是确实是得移动这么多，才能重合。 $theta$的话，就是关节转动的角度了，后面几个关节，可能初始角度得加一个180°才行。 这个DH参数值拿到了之后，就得想办法拿到转换矩阵了。 好在《机器人学导论》这本书里直接给了计算公式：

矩阵变换公式：

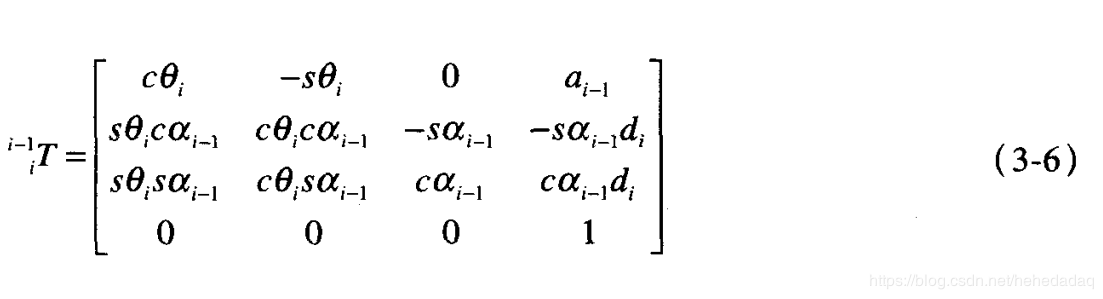
这玩意儿还得配套几个公式才行。

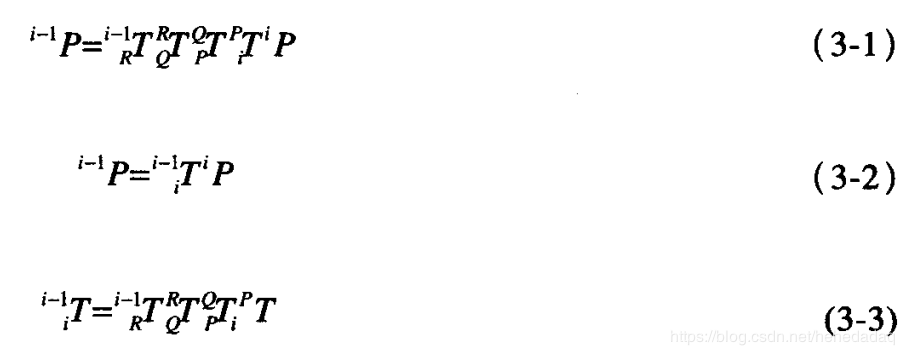
总之拿到了DH参数，就把表里的值代入到T中， 然后连乘，就能计算出末端位姿了。

最后直接上代码吧：

from