机器学习（九）：k-均值（k-means）

更多内容关注公众号：数学的旋律

tb店铺搜：FUN STORE玩物社，专业买手挑选送礼好物

引言

    k均值（k-means）是一种聚类算法，其工作流程如下：随机选择k个点作为初始质心（质心即簇中所有点的中心），然后将数据集中的每个点分配到一个簇中，具体来讲，为每个点找距其最近的质心，并将其分配给该质心所对应的簇。这一步完成之后，每个簇的质心更新为该簇所有点的平均值。重复以上步骤，直到质心不发生变化。
    k均值的操作解释参见图1。

图1

    然而随机地选取初始质心，簇的质量常常很差，为克服该问题，有人提出了二分k均值（bisecting k-means）算法，该算法不太受初始化问题的影响。
    本文讨论欧氏空间中的聚类问题，所用距离为欧氏距离（在kNN中已介绍过欧氏距离，这里不再重述）。

一、基本k均值算法

    k均值是发现给定数据集的k个簇的算法。簇个数k是用户给定的，每一个簇通过其质心（centroid），即簇中所有点的中心来描述。
    k均值的基本算法如下：首先，随机选择k个初始质心，其中k即所期望的簇的个数。每个点指派到最近的质心，而指派到一个质心的点集为一个簇。然后，根据指派到簇的点，更新每个簇的质心。重复指派和更新步骤，直到簇不发生变化，或等价地，直到质心不发生变化。
算法1 基本k均值算法

选择k个点作为初始质心
repeat
    将每个点指派到最近的质心，形成k个簇
    重新计算每个簇的质心
until 质心不发生变化

二、目标函数

    前面说到，k个初始质心是随机选择的，不同的选择可能产生不同的结果，如图2所示，经过两次迭代，不同的初始质心得出(a)(b)两种不同结果。

图2

    如何才能知道生成的簇哪个比较好呢？我们使用误差的平方和（Sum of the Squared Error,SSE）作为度量聚类质量的目标函数。我们计算每个数据点的误差，即它到最近质心的欧氏距离，然后计算误差的平方和。SSE形式地定义如下：$$SSE=\sum _{i=1}^k\sum _{x\in C_i}dist(c_i,x{)}^2$$其中，dist是欧氏空间中两个对象之间的标准欧氏距离。若数据集为 D = { x 1 , x 2 , ⋯   , x i , ⋯   , x N } D=\{x_1,x_2,\cdots,x_i,\cdots,x_N\} D={x1​,x2​,⋯,xi​,⋯,xN​}其中$x_i=({x_i}^{(1)},{x_i}^{(2)},\cdots ,{x_i}^{(i)},\cdots ,{x_i}^{(n)}{)}^T$，$x^{(i)}$表示$x$的第$i$个特征的取值，则$$dist(x_i,x_j)=(\sum _{l=1}^n|{x_i}^l-{x_j}^{(l)}{|}^2{)}^{\frac{1}{2}}$$
$C_i$表示第i个簇，$c_i=\frac{1}{m}{\sum }_{x\in C_i}x$为簇$C_i$的质心，$m_i$为第$i$个簇中对象的个数。k均值的目标函数就是最小化SSE。
    SSE值越小表示数据点越接近于它们的质心，聚类效果也越好。一种肯定可以降低SSE值的方法是增加簇的个数，但这违背了聚类的目标，聚类的目标是在簇数目不变的情况下提高簇的质量。
例1
3个二维点$(1,1)$、$(2,3)$和$(6,2)$的质心是$(\frac{(1+2+6)}{3},\frac{(1+3+2)}{3})=(3,2)$。

三、二分k均值

    在目标函数一节中，我们知道，选择适当的初始质心是基本k均值过程的关键步骤。常见的方法是随机选取初始质心，但是簇的质量常常很差。
    为了克服这个问题，有人提出了二分k均值算法。该算法是基本k均值算法的直接扩充，基本思路如下：
    首先，将所有点作为一个簇，然后在该簇上使用基本k均值算法，其中k=2，从而将该簇一分为二。之后选择其中一个簇继续进行同样的划分，选择哪一个簇进行划分取决于对其划分是否可以最大程度降低SSE值。上述基于SSE的划分过程不断重复，直到得到用户指定的簇数目为止。
算法2 二分k均值算法

初始化簇表，使之包含由所有的点组成的簇。
repeat
    从簇表中取出一个簇（选取对其划分能最大程度降低SSE值的簇）。
    {对选定的簇进行多次二分“试验”}
	for i=1 to 试验次数 do
	    使用基本k均值，二分选定的簇。
	end for
    从二分试验中选择具有最小总SSE的两个簇。
    将这两个簇添加到簇表中。
until 簇表中包含k个簇。

    该算法不太受初始化问题的影响，因为它执行了多次二分试验并选取具有最小SSE的试验结果，还因为每步只有两个质心。
例2
    下图3展示二分k均值如何找到4个簇。迭代1找到了两个簇对，迭代2分裂了最右边的簇对，迭代3分裂了最左边的簇对。

图3

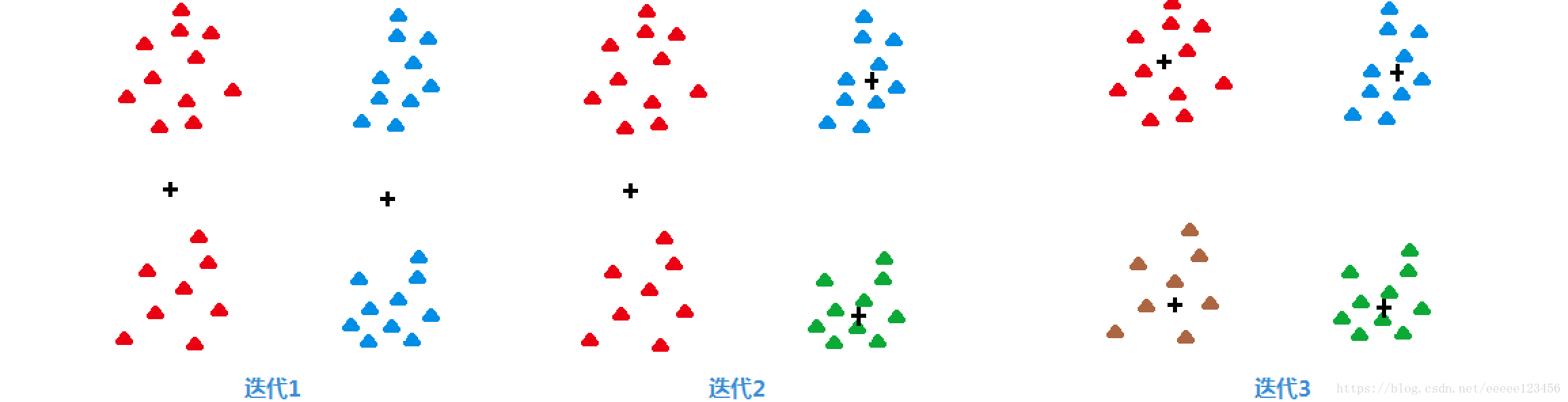
四、优点与缺点

    k均值简单并且可以用于各种数据类型。它相当有效，尽管常常多次运行。k均值的某些变种（包括二分K均值）甚至更有效，并且不太受初始化问题的影响。然而，k均值并不适合所有的数据类型。它不能出来非球形簇、不同尺寸和不同密度的簇。最后，k均值仅限于具有中心（质心）概念的数据。

五、代码实现（python）

以下代码来自Peter Harrington《Machine Learing in Action》。
本例代码实现二分k均值算法。
代码如下（保存为kMeans.py)：

# -- coding: utf-8 --
from numpy import *

def loadDataSet(fileName):
    # 获取数据集
    dataMat = []
    fr = open(fileName)
    for line in fr.readlines():
        curLine = line.strip().split('\t')
        fltLine = map(float,curLine)
        dataMat.append(fltLine)
    return dataMat

def distEclud(vecA, vecB):
    # 根据式()计算vecA, vecB两点间的欧氏距离
    return sqrt(sum(power(vecA - vecB, 2)))

def randCent(dataSet, k):
    # 随机生成k个质心
    n = shape(dataSet)[1]                         # 获取数据集特征数量，即列数
    centroids = mat(zeros((k,n)))                 # 初始化一个k行n列的矩阵，元素为0，用于存储质心
    for j in range(n):
        minJ = min(dataSet[:,j])                  # 获取数据集第j列的最小值
        rangeJ = float(max(dataSet[:,j]) - minJ)  # 计算数据集第j列中，最大值减最小值的差
        # 随机生成k行1列的数组，元素在0到1之间，乘以rangeJ再加上minJ，则可得随机生成的第j列中最小值与最大值之间的一个数
        centroids[:,j] = mat(minJ + rangeJ * random.rand(k,1))
    return centroids

def kMeans(dataSet, k, distMeas=distEclud, createCent=randCent):
    # kMeans函数接受4个输入参数，数据集及簇的数目为必选参数，计算距离默认为欧氏距离，创建初始质心默认为随机生成
    m = shape(dataSet)[0]                         # 获取数据集数量，即行数
    clusterAssment = mat(zeros((m,2)))            # 初始化一个m行2列的矩阵，元素为0，第一列存储当前最近质心，第二列存储数据点与质心的距离平方
    centroids = createCent(dataSet, k)            # 创建k个初始质心
    clusterChanged = True
    while clusterChanged:
        clusterChanged = False
        for i in range(m):
            # 循环m个数据，寻找距离第i个数据最近的质心
            minIndex = -1                         # 初始化最近质心
            minDist = inf                         # 初始化第i个数据与最近质心的最小距离为无穷大
            for j in range(k):
                # 循环k个质心，寻找离第i个数据最近的质心
                distJI = distMeas(centroids[j,:],dataSet[i,:]) #计算第i行数据与第j个质点的欧氏距离
                if distJI < minDist:
                    minIndex = j                  # 更新最近质心为第j个
                    minDist = distJI              # 更新第i个数据与最近的质心的最小距离
            if clusterAssment[i,0] != minIndex: clusterChanged = True         # 若其中clusterAssment存储的质心与此次结果不一样，则需迭代，直至没有质心的改变
            clusterAssment[i,:] = minIndex,minDist**2    # 更新clusterAssment数据
        for cent in range(k):
            ptsInClust = dataSet[nonzero(clusterAssment[:,0].A==cent)[0]]     # 获取属于第cent个质心的所有数据
            centroids[cent,:] = mean(ptsInClust, axis=0) # 计算属于第cent个质心的所有数据各列的平均值，更新第cent个质心
    return centroids, clusterAssment              # centroids为当前k个质心，clusterAssment为各个数据所属质心及距离该质心的距离平方

def biKmeans(dataSet, k, distMeas=distEclud):
    # biKmeans函数接受3个输入参数，数据集及簇的数目为必选参数，计算距离默认为欧氏距离
    m = shape(dataSet)[0]                         # 获取数据集数量，即行数
    clusterAssment = mat(zeros((m,2)))            # 初始化一个m行2列的矩阵，元素为0，第一列存储当前最近质心，第二列存储数据点与质心的距离平方
    centroid0 = mean(dataSet, axis=0).tolist()[0] # 将所有点作为一个簇，计算数据集各列的平均值，作为初始簇的质心
    centList = [centroid0]                        # centList存储各个质心
    for j in range(m):
        clusterAssment[j,1] = distMeas(mat(centroid0), dataSet[j,:])**2        # 计算初始质心与各数据的距离平方
    while (len(centList) < k):
        # 未达到指定簇的数目，则继续迭代
        lowestSSE = inf
        for i in range(len(centList)):
            # 循环簇的个数，寻找使SSE下降最快的簇的划分
            ptsInCurrCluster = dataSet[nonzero(clusterAssment[:,0].A==i)[0],:] # 获取属于第i个质心的所有数据
            centroidMat, splitClustAss = kMeans(ptsInCurrCluster, 2, distMeas) # 将第i个簇二分为2个簇
            sseSplit = sum(splitClustAss[:,1])                                 # 计算第i个簇二分为2个簇后的SSE值
            sseNotSplit = sum(clusterAssment[nonzero(clusterAssment[:,0].A!=i)[0],1]) # 计算剩余数据的SSE值
            if (sseSplit + sseNotSplit) < lowestSSE:
                # 若二分后总体SSE值下降，则更新簇的信息
                bestCentToSplit = i
                bestNewCents = centroidMat         # 第i个簇二分后的质心
                bestClustAss = splitClustAss.copy()# 第i个簇二分后的结果
                lowestSSE = sseSplit + sseNotSplit # 更新当前SSE值
        bestClustAss[nonzero(bestClustAss[:,0].A == 1)[0],0] = len(centList)   # 更新簇的分配结果，将二分后第二个簇分配到新簇
        bestClustAss[nonzero(bestClustAss[:,0].A == 0)[0],0] = bestCentToSplit # 更新簇的分配结果，将二分后第一个簇分配到被划分簇
        centList[bestCentToSplit] = bestNewCents[0,:].tolist()[0]              # 更新簇的分配结果，更新未划分簇质心为二分后第一个簇的质心
        centList.append(bestNewCents[1,:].tolist()[0])                         # 更新簇的分配结果，添加新质心为二分后第二个簇的质心
        clusterAssment[nonzero(clusterAssment[:,0].A == bestCentToSplit)[0],:]= bestClustAss # 将被划分簇数据更新为划分后簇
    return mat(centList), clusterAssment

数据集格式如下（保存为testSet.txt）：

3.275154	2.957587
-3.344465	2.603513
0.355083	-3.376585
1.852435	3.547351
-2.078973	2.552013
-0.993756	-0.884433

运行命令如下：










以上全部内容参考书籍如下：
《数据挖掘导论（完整版）》人民邮电出版社
Peter Harrington《Machine Learing in Action》