浅谈数据结构排序算法之（一）——冒泡排序

所谓排序就是指：假设含有n个记录的序列为{r1,r2,……rn},其对应的关键字分别为{k1,k2,……kn},需确定1,2,……n的一种排列p1,p2,……pn,使其相应的关键字满足kp1<=kp2<=……kpn(非递减或非递增)关系，即使得序列成为一个按关键字有序的序列{rp1,rp2,……rpn},这样的操作就称为排序。

我们在排序的时候，通常将数据元素称为记录。显然我们输入的是一个记录集合，输出的也是一个记录集合，所以我们可以将排序看成是线性表的一种操作。

2.排序的稳定性评估

假设ki = kj( 1 < = i <= n,1<=j<=n,i!= j)，且在排序前的序列中ri领先于rj(即i < j)。如果排序后ri仍然领先于rj,则称所用的排序方法是稳定的；反之，若可能使得排序后的序列中rj领先于ri,则称所用的排序方法是不稳定的。

3. 内排序与外排序

根据在排序过程中待排序的记录是否全部被置放在内存中，排序分为：内排序与外排序。

内排序是在排序整个过程中，待排序的所有记录全部被放置在内存中。外排序是由于排序的记录个数太多，不能同时放置在内存，整个排序过程需要在内外存之间多次交换数据才能进行。对于内排序来说，排序算法的性能主要受3个方面的影响。

时间性能：高效率的内排序算法应该是具有尽可能少的关键字比较和尽可能少的记录移动次数。
辅助空间：评估排序算法的另一个主要标准是执行算法所需要的辅助存储空间。辅助存储空间是除了存放待排序所占用的存储空间之外，执行算法所需要的其他存储空间。
算法复杂性：指算法本身的复杂度。根据排序过程中借助的主要操作，我们把内排序分为：插入排序、交换排序、选择排序和归并排序。

在众多的排序算法里，冒泡排序思路最简单，也最容易理解，本篇就以冒泡排序开始说起。

二.冒泡排序

1.基本定义

冒泡排序（Bubble Sort）是一种交换排序，它的基本思想是：两两比较相邻记录的关键字，如果反序则交换，直到没有反序的记录为止。

2.最简单的交换排序

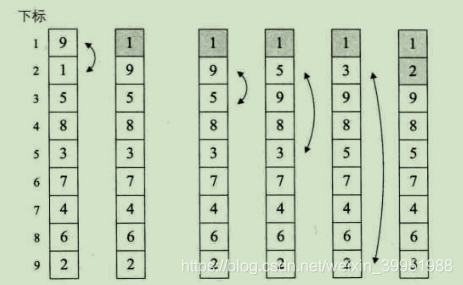
让每一个关键字，都和它后面的每一个关键字比较，如果大则交换，这样第一位置的关键字在第一次循环之后一定变成最小值，后面顺序以此类推，如图所示：

3.正宗的冒泡排序

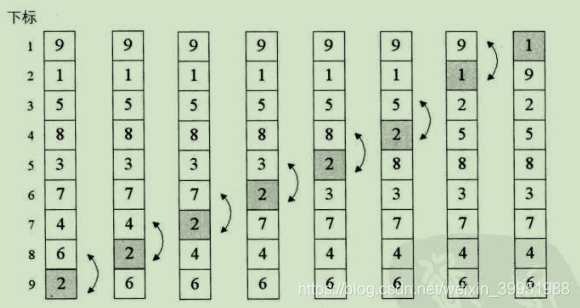
假设我们待排序的关键字序列是{9,1,5,8,3,7,4,6,2}，当i=1时，变量j由8反向循环到1，逐个比较，将较小值交换到前面，直到最后找到最小值放置在了第一的位置，如图所示：

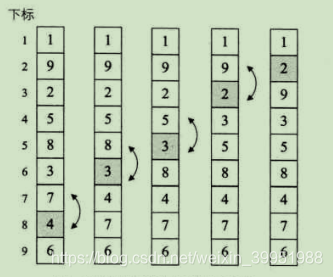
当i = 2时，变量j由8反向循环到2，逐个比较，在将关键字2交换到第二位置的同时，也将关键字4和3有所提升。后面的步骤依次比较交换

4.优化升级版的冒泡排序

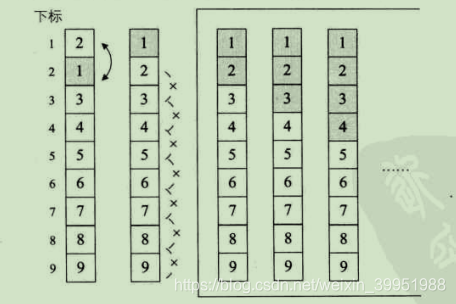
前面这样的冒泡排序是否还可以优化呢？当然啦。这样试想一下，如果我们待排序的序列是{2,1,3,4,5,6,7,8,9}，也就是说，除了第一和第二的关键字需要交换外，别的都是正常顺序。当i = 1时，交换了2和1，此时序列已经有序，后面的循环不需要再次进行了。

三.实例代码

首先我们定义一个结构和一个交换函数，供后面排序算法调用：

const int SIZE = 10;
struct ListTag
{
	int data[SIZE + 1];
	int length;
};
inline void Swap(ListTag *listTag,const int i,const int j)
{
	int temp = listTag->data[i];
	listTag->data[i] = listTag->data[j];
	listTag->data[j] = temp;
}

1.简单的交换排序

void BuddleSort1(ListTag *listTag)
{
	int i,j;
	for(int i = 1;i < listTag->length;i++)
	{
		for(j = i + 1;j <= listTag->length;j++)
		{
			if(listTag->data[i] > listTag->data[j])
			{
				Swap(listTag,i,j);    //交换listTag->data[i]和listTag->data[j]的值
			}
		}
	}
}

2.正宗的冒泡排序

void BuddleSort2(ListTag *listTag)
{
	int i,j;
	for(int i = 1;i < listTag->length;i++)
	{
		for(j = listTag->length;j >= i;j--)     //从后往前循环
		{
			if(listTag->data[j] > listTag->data[i])  //若前者大于后者
			{
				Swap(listTag,j,j+1);    //交换listTag->data[j]和listTag->data[j + 1]的值
			}
		}
	}
}

3.优化后的冒泡排序

void BuddleSort3(ListTag *listTag)
{
	int i,j;
	bool flag = true;    //用flag作为标记
	for(int i = 1;i < listTag->length && flag;i++)
	{
		flag = false;
		for(j = listTag->length - 1;j >= i;j--)     //从后往前循环
		{
			if(listTag->data[j] > listTag->data[j + 1])  //若前者大于后者
			{
				Swap(listTag,j,j+1);    //交换listTag->data[j]和listTag->data[j + 1]的值
				flag = true;            //如果有数据交换，则flag为true
			}
		}
	}
}