数据结构浅浅析之（三）——树（Tree）（下篇——应用提高附C++代码）

最新推荐文章于 2024-11-01 17:07:39 发布

原创最新推荐文章于 2024-11-01 17:07:39 发布 · 661 阅读

2 ·

CC 4.0 BY-SA版权

文章标签：

#树 #数据结构 #C/C++/Qt #设计模式 #设计思想

【菜鸟驿站】Learn数据结构-基础知识专栏收录该内容

5 篇文章

订阅专栏

本文深入探讨二叉树的顺序与链式存储结构，通过C++代码实例展示二叉树的创建与四种遍历方法，同时介绍二叉树在更复杂树型结构中的应用。

一.写在前面

本篇文章紧随上篇文章《数据结构浅浅析之（三）——树（Tree）（上篇——基础知识）》之后。假设现在我们已经了解了数据结构的有关树（tree）的基本知识。如果不太清楚树的基本知识，建议先去看看上篇有关树的基础知识篇一文。本篇文章以树型结构中最简单的二叉树（Binary Tree）说起。

二.二叉树的存储结构

1.二叉树的顺序存储结构

二叉树的顺序存储结构就是用一维数组存储二叉树树中的结点，数组的下标要能体现出结点的逻辑关系，比如双亲结点与孩子的关系，左右兄弟的关系等等。

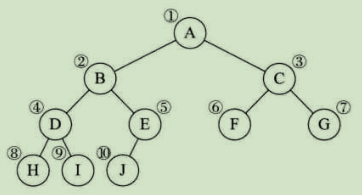
首先我们来看看一棵完全二叉树的顺序存储，一棵完全二叉树如图所示：

一棵完全二叉树

将这棵二叉树存入到数组中后相应的下标对应相同的位置，如图所示：

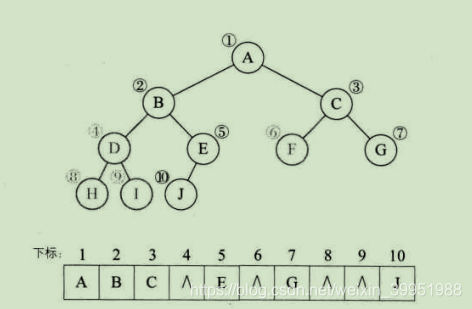
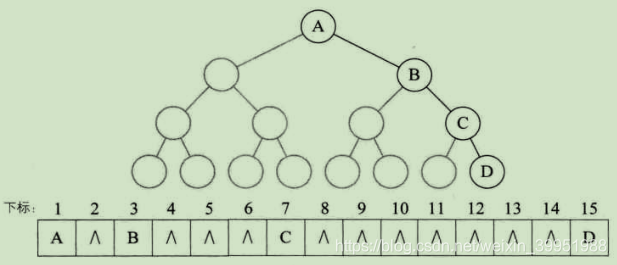
如果是一般的二叉树（不是完全二叉树），啊哈……，怎么办？有人提出这样的设想：我们可以按其完全二叉树进行编号，只不过，将不存在的结点设置为“∧”，（这个叫“有人”的人真是个天才）如图所示（浅色的结点表示不存在此结点）

Perfect！！完美的解决了这个问题，如果……我是说如果遇到这种情况呢：一棵深度为k的右斜树，它只有k个结点，那我么的存储方式就如下所示：

Emmmmmmmm……，我们开辟了15个存储空间，里面只存储了四个元素，内存不要钱啊？！！！！很显然，这个“有人”的想法是好的，但是不是很实用，最起码遇到这种情况不适用，如果深度足够大，浪费内存浪费的厉害，既然顺序存储适用性不强，那我们在看看链式存储方式。

2.二叉树的链式存储结构

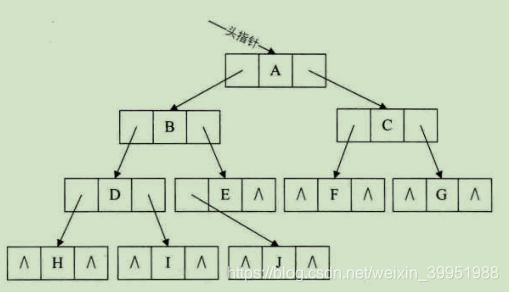
二叉树每个结点最多两个孩子，所以为它设计一个数据域和两个指针域是比较大众的想法，我们称这样的链表为二叉链表。如图所示：

三.代码实例

首先我们得有一个树结点，定义如下：

struct TreeNode
{
	char data;
	TreeNode* LeftNode;     //左结点
	TreeNode* RightNode;    //右结点
};

然后我们定义我们的树类，里面包含获取树高和四种遍历树的方法等：

tree.h:

enum ORDERTYPE
{
	PREORDER    = 1,  //前序遍历
	MIDDLEORDER = 2,  //中序遍历
	POSTORDER   = 3,  //后序遍历
	LEVELORDER  = 4   //层次遍历
};

class Tree{
public:
	Tree():m_root(NULL),m_height(0){}
	~Tree(){}

public:
	///按照前序遍历序列创建二叉树
	void createTree(string s);

	//遍历二叉树
	void OrderBinaryTree(const ORDERTYPE orderType);

	//获取树高
	const int getHeightBinaryTree();

private:
	//前序遍历
	void preOrder(TreeNode * node);
	//中序遍历
	void inOrder(TreeNode * node);
	//后序遍历
	void postOrder(TreeNode * node);
	//层次遍历
	void levelOrder();
	//创建树结点
	TreeNode* createNode(string &s ,unsigned pos);
	//获取树的高度
	void getHeight(TreeNode * node,int h); 
private:
	TreeNode * m_root;
	int m_height;
};

具体实现方法如下：

tree.cpp:

void Tree::createTree(string s)
{
	int pos = -1;
	m_root=createNode(s,pos);
}

void Tree::OrderBinaryTree(const ORDERTYPE orderType)
{
	switch(orderType)
	{
	case PREORDER: preOrder(m_root);  std::cout<<endl; break;  //前序遍历

	case MIDDLEORDER:inOrder(m_root); std::cout<<endl; break;  //中序遍历

	case POSTORDER:postOrder(m_root); std::cout<<endl; break;  //后序遍历

	case LEVELORDER:levelOrder(); break;                       //层次遍历

	default:break;
	}
}

void Tree::levelOrder()
{
	if(m_root==NULL)
	{
		return;
	}	
	queue<TreeNode*> treeQueue;
	treeQueue.push(m_root);
	while(!treeQueue.empty())
	{
		TreeNode * node;
		node=treeQueue.front();
		treeQueue.pop();
		cout<<node->data<<' ';
		if(node->LeftNode!=NULL)
		{
			treeQueue.push(node->LeftNode);
		}
		if(node->RightNode!=NULL)
		{
			treeQueue.push(node->RightNode);
		}
	}
	cout<<endl;
}

const int Tree::getHeightBinaryTree()
{
	getHeight(m_root,0);
	return m_height;
}

void Tree::preOrder(TreeNode * node)
{
	if(node!=NULL)
	{
		std::cout<<node->data<<' ';
		preOrder(node->LeftNode);
		preOrder(node->RightNode);
	}
}

void Tree::inOrder(TreeNode * node)
{
	if(node!=NULL)
	{
		inOrder(node->LeftNode);
		std::cout<<node->data<<' ';
		inOrder(node->RightNode);
	}
}

void Tree::postOrder(TreeNode * node)
{
	if(node!=NULL)
	{
		postOrder(node->LeftNode);
		postOrder(node->RightNode);
		std::cout<<node->data<<' ';
	}
}

TreeNode* Tree::createNode(string &s,unsigned pos)
{
	++pos;
	TreeNode* treeNode;
	if(pos >= s.size())
	{
		return NULL;
	}	
	else{
		if(s[pos]=='#')
		{
			treeNode=NULL;
		}

		else{
			treeNode=new TreeNode;
			treeNode->data=s[pos];
			treeNode->LeftNode=createNode(s,pos);
			treeNode->RightNode=createNode(s,pos);
		}
		return treeNode;
	}
}

void Tree::getHeight(TreeNode * node,int h)
{
	if(node!=NULL)
	{
		++h;
		if(h>m_height)
		{
			m_height = h; 
		}
		getHeight(node->LeftNode,h);
		getHeight(node->RightNode,h);
	}
}

然后在主函数中进行测试：

int _tmain(int argc, _TCHAR* argv[])
{
	Tree tree;
	string s  = "ABD##E#F##C##";   //#代表空结点
	tree.createTree(s);
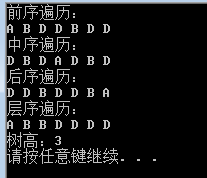
	cout<<"前序遍历："<<endl;
	tree.OrderBinaryTree(PREORDER);
	cout<<"中序遍历："<<endl;
	tree.OrderBinaryTree(MIDDLEORDER);
	cout<<"后序遍历："<<endl;
	tree.OrderBinaryTree(POSTORDER);
	cout<<"层序遍历："<<endl;
	tree.OrderBinaryTree(LEVELORDER);
	cout<<"树高：" << tree.getHeightBinaryTree() << endl;
	system("pause");
	return 0;
}

输出结果如下：

四.二叉树的扩展

二叉树是我们树型结构中最简单的一种。了解了二叉树的基本逻辑，如果要实现三叉树、四叉树、八叉树等等，原理和这一样。比如图像识别算法里，我们对图像识别时一般是对像素进行操作，通过卷积运算对像素进行处理提取，如果我们以9*9像素矩阵作为我们的基本单元，最方便的莫过于定义一个9叉树结构，像下面这样：

9*9像素矩阵

定义的九叉树结构：

struct ImageTreeNode
{
	unsigned data;                 //像素值
	ImageTreeNode*   LeftTop;      //左上
	ImageTreeNode*   MidTop;       //中上
	ImageTreeNode*   RightTop;     //右上 
	ImageTreeNode*   MidLeft; 	   //中左
	ImageTreeNode*   MidMid; 	   //中中
	ImageTreeNode*   MidRight; 	   //中右
	ImageTreeNode*   BottomLeft;   //底左
	ImageTreeNode*   BottomMid;    //底中
	ImageTreeNode*   BottomRight;  //底右
};

具体实现有兴趣可以研究一下。

【上一篇：】数据结构浅浅析之（三）——树（Tree）（上篇——基础知识附C++代码）：

https://blog.youkuaiyun.com/weixin_39951988/article/details/86534298