matlab 欧拉法解微分方程组_学习随笔之龙格库塔法解常微分方程

设一阶微分方程及初值为：

1. 欧拉法

过点(x0,y0)以y’(x0)=f(x0,y0)为斜率作切线，切线方程：

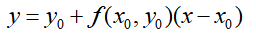
欧拉法即是f(x,y)在(x0,y0)处的一阶泰勒展开，即有：

设x0,x1,x2,…xn的步长为h，则欧拉法求解的公式可表示为：

欧拉法具有一阶精度，其局部阶段误差是关于步长的二阶无穷小量。

1. 改进欧拉法

由微分中值定理，改进欧拉方程为：

由于等式两边都存有yn+1未知量，这种形式称为隐式形式。因为是近似计算，可以由欧拉公式求得yn+1的一个近似值（预报值），然后将其带入公式中再进行计算得到一个yn+1值（校正值）。（本文中公式所有的方框都为*号，显示问题）

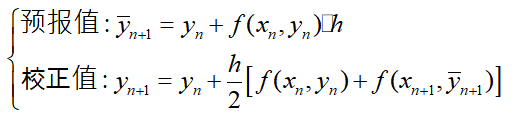
写成一个公式即为：

改进欧拉法具有二阶精度，其局部阶段误差是关于步长的三阶无穷小量。

1. 龙格库塔法

根据微分中值定理，在(xn,xn+1)区间存在一个ζ满足：

称ζ处的斜率f(ζ,y(ζ))为平均斜率K，则有：

显然，取xn处的斜率f(xn,yn)为K时即为欧拉法，取xn和xn+1处的斜率均值为K时为改进欧拉法。若在[xn,xn+1]区间多取几个点的斜率，以其某种加权均值作为K，可进一步提升yn+1精度。

在[xn,xn+1]区间取m个点，其中第j个点及对应的斜率Kj为：

每个斜率Kj的加权值为λj，则平均斜率K及yn+1估值为：

此即为龙格库塔算法，选取恰当的αj,βj和λj可使算法精度尽可能提升，算法阶数由取点数m决定，阶数越高精度越高。

二阶龙格库塔公式：

三阶龙格库塔公式：

四阶龙格库塔公式：

Matlab代码

clear
clc
close all
%% 初始条件
syms x y f;          % 原方程为y=e^(sinx)
f(x,y) = y*cos(x); % 条件1：方程导数y'=f(x,y)
x0 = 0;
y0 = 1;            % 条件2：初值y(0)=1

h = 0.2;           % 步长
x = x0:h:10;       % x取值范围
y = exp(sin(x));    % 真实的y值（待求）
len = length(x);

%% 欧拉法
y1 = zeros(size(x)); % 初始化y
y1(1) = y0;
for ii = 2:len
    K1 = f(x(ii-1),y1(ii-1));
    y1(ii) = y1(ii-1) + h*K1;
end

%% 二阶龙格库塔
y2 = zeros(size(x)); % 初始化y
y2(1) = y0;
for ii = 2:len
    K1 = f(x(ii-1),y2(ii-1));
    K2 = f(x(ii-1)+h/2,y2(ii-1)+h*K1/2);
    y2(ii) = y2(ii-1) + h*K2;
end

%% 三阶龙格库塔
y3 = zeros(size(x));
y3(1) = y0;
for ii = 2:len
    K1 = f(x(ii-1),y3(ii-1));
    K2 = f(x(ii-1)+h/2,y3(ii-1)+h*K1/2);
    K3 = f(x(ii-1)+h,y3(ii-1)+h*(K2*2-K1));
    y3(ii) = y3(ii-1) + h*(K1+4*K2+K3)/6;
end

%% 四阶龙格库塔
y4 = zeros(size(x));
y4(1) = y0;
for ii = 2:len
    K1 = f(x(ii-1),y4(ii-1));
    K2 = f(x(ii-1)+h/2,y4(ii-1)+h*K1/2);
    K3 = f(x(ii-1)+h/2,y4(ii-1)+h*K2/2);
    K4 = f(x(ii-1)+h,y4(ii-1)+h*K3);
    y4(ii) = y3(ii-1) + h*(K1+2*K2+2*K3+K4)/6;
end

%% 绘图
figure
plot(x,y,x,y2,x,y3,x,y4,x,y1)
title('fontname{微软雅黑}fontsize{10}龙格库塔求解值');
xlabel('fontname{微软雅黑}fontsize{10}x');
ylabel('fontname{微软雅黑}fontsize{10}y');
legend('原值','2阶值','3阶值','4阶值','欧拉法')

figure
plot(x,y2-y,x,y3-y,x,y4-y,x,y1-y)
title('fontname{微软雅黑}fontsize{10}龙格库塔误差');
xlabel('fontname{微软雅黑}fontsize{10}x')
ylabel('fontname{微软雅黑}fontsize{10}');
legend('2阶误差','3阶误差','4阶误差','欧拉法')

(早期随笔文件补档)