源码解析_Python Numpy gradient源码解析

最新推荐文章于 2024-09-22 14:53:45 发布
最新推荐文章于 2024-09-22 14:53:45 发布
阅读量251 收藏
点赞数
CC 4.0 BY-SA版权
文章标签： 源码解析
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.youkuaiyun.com/weixin_39944515/article/details/112722296
本文深入探讨了Numpy的gradient函数，该函数用于计算数组的梯度。主要内容包括一维和多维数组的梯度计算，边缘处理选项，以及一阶和二阶中心差分公式。博客指出，尽管文档提到中间元素使用2阶中心差分，但实际上默认使用一阶中心差分。此外，边缘处理可以通过edge_order参数调整。文章适合对数值计算和Numpy感兴趣的读者。

摘要生成于 C知道 ，由 DeepSeek-R1 满血版支持， 前往体验 >

复习图像梯度，发现Numpy有一个梯度计算函数，解析它的源码和需要注意的问题，最后自定义一个梯度函数

Numpy提供了数组梯度计算函数

gradient(f, *varargs, **kwargs)

输入

必选参数：类N维数组（列表/元组/数组）

可选参数：标量列表或数组列表，用于计算差分时的间隔空间

单个标量：为所有轴指定间隔

N个标量：为每一轴指定了间隔，比如dx, dx, dz...

N个数组：为f的每一轴都指定了采样值的下标，每个数组的长度必须匹配相对应那一维的长度

N个标量或数组的组合，其作用等同于2和3

注意：如果关键字参数axis被指定，那么这个可选参数的长度必须和要计算的轴数一致

关键字参数有2个：

edge_order：在边界使用第N-阶差分公式，默认是1-阶

axis：None或者是整数又或者是整数的元组，表示沿着指定的轴计算梯度，默认为None，表示计算所有轴的梯度。如果输入为负数，表示从后向前计算轴的梯度

从它的介绍中，我唯一没理解的就是可选参数的用法，看了代码后也没理解，因为它和一阶差分没有关系，所以在后面的内容就忽略对可选参数的解析

输出

如果输入是一维数组，返回同样大小的梯度数组

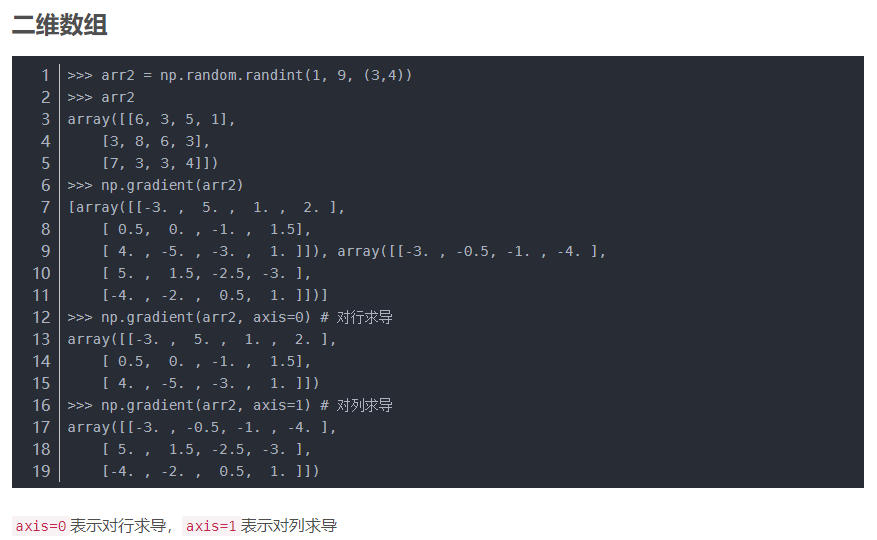
如果是多维数组，并要求计算多维，那么返回一个列表，包含计算的每一维的梯度，其大小和输入数组一致

计算方式

在它的介绍中，中间元素使用**2阶中心差分**，但是查看源码发现，它默认使用的其实是一阶中心差分，除非输入可选参数的3和4选项，但是代码中的二阶差分公式也没看懂？，应该是使用泰勒级数的近似公式，所以跳过对代码中二阶差分的介绍

两边使用一阶前向或后向差分，也可通过关键字参数edge_order修改计算方式

差分公式

一阶前向差分：

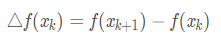
42e023b28fbc95501ccb920e690cb2c7.png

一阶后向差分：

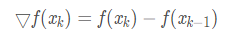
299006317e5ee57bc26217cb42f6fae0.png

一阶中心差分：

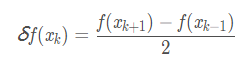
7f3a00f19447282b7a9303037d21c6d1.png

二阶中心差分：

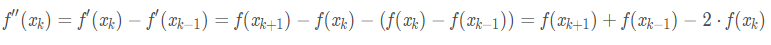
334cfcadb9e34b7457c25e6839b57703.png

3939c505e4a6002dd71e6c6989b50438.png

133c0653356c3146158a7d3a3fb93f94.png

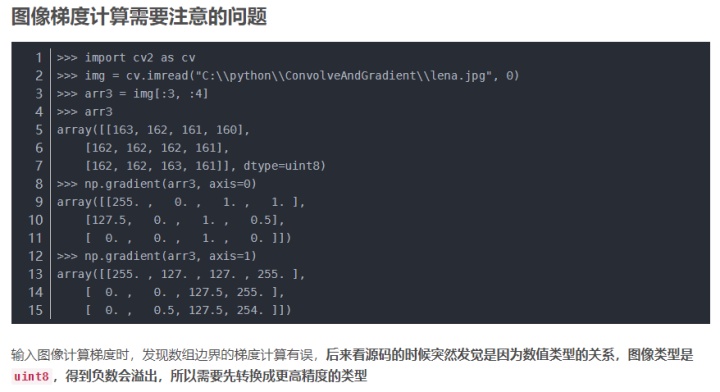
f298c62e783a886a75082173b54e0fc1.png

cef801e8b1c19c7ec67925ad620600db.png

源码分析见：

https://blog.youkuaiyun.com/u012005313/article/details/84035371​blog.youkuaiyun.com
python之numpy详细分析（附代码）
码农研究僧的博客
06-29 2882
前言 1.Numpy (Numerical Python)是一个开源的Python科学计算库，用于快速处理任意维度的数组。 2.Numpy支持常见的数组和矩阵操作。对于同样的数值计算任务，使用Numpy比直接使用Python要简洁的多。 3.Numpy使用ndarray对象来处理多维数组，该对象是一个快速而灵活的大数据容器。 ...
numpy-ml 决策树源码分析
using namespace 数学工具构造器;
01-26 468
源码： numpy_ml/trees/dt.py 文档： Tree-based models DecisionTree 写一个入口代码进行调试 from sklearn.datasets import load_iris from sklearn.metrics import accuracy_score from sklearn.model_selection import train_test_split from numpy_ml.trees import DecisionTree X, y =
NumPy源码解析
wq_0708的博客
01-15 2125
NumPy源码初步解析
NumPy 源码解析（一）
龙哥盟
07-05 488
【代码】NumPy 源码解析（一）
numpy基础全覆盖源代码手把手教你numpy计算
03-21
numpy基础全覆盖源代码手把手教你numpy计算，numpy基础全覆盖源代码手把手教你numpy计算
python 卷积神经网络 源码解析_代码详解：最全面的卷积神经网络介绍，都在这里了...
weixin_39988888的博客
12-15 1392
全文共8600字，预计学习时长40分钟或更长源：pexels.com神经网络由具有权重和偏差的神经元组成。通过在训练过程中调整这些权重和偏差，以提出良好的学习模型。每个神经元接收一组输入，以某种方式处理它，然后输出一个值。如果构建一个具有多层的神经网络，则将其称为深度神经网络。处理这些深度神经网络的人工智能学分支被称为深度学习。普通神经网络的主要缺点是其忽略了输入数据的结构。在将数据馈送到神经网络...
MADDPG多智能体博弈对抗算法Python源码解析
6. Python编程: 资源中的源码是用Python编写的，因此需要熟悉Python语言及其相关库，如NumPy、TensorFlow或PyTorch，这些库在深度学习和强化学习算法的实现中经常被使用。 7. 代码注释: 详细注释的代码对于理解和...
大模型底层 transformers源码解析之trainer.py
强化学习曾小健
04-17 4260
我会根据你提供的trainer.py源代码,用python的Graph包画出流程图,并着重介绍train()方法。- 将 inputs 通过 self._prepare_inputs 方法处理后传给 self.training_step。- 调用 optimizer.step() 和 lr_scheduler.step() 进行参数更新。计算总共需要训练的步数 max_steps 和 num_train_epochs。- 每 args.logging_steps 个步骤打印训练日志。
metabalance源码解析
最新发布
baidu_39157459的博客
09-22 390
这段代码实现了算法，是一种自定义的优化器，它继承了 PyTorch 中的Optimizer类。主要的目的是通过调整多个损失函数的梯度大小，使得主梯度和辅助梯度之间的差距缩小，从而实现平衡。
数据竞赛中XGB模型的Python实现及源码解析
- Python作为数据科学的主要编程语言，它有着丰富的数据处理和机器学习库，比如NumPy、Pandas、Matplotlib、Scikit-learn和XGBoost等，这些库使得数据预处理、分析和模型构建变得容易。 - 在数据竞赛中，Python的...
numpy 基础代码
08-24
python 中 numpy 基础代码,
numpy数据分析源代码+大数据的读取_.ipynb
02-14
blog链接：https://blog.youkuaiyun.com/qq_35456045/article/details/104319408 详细的，有解释的源代码哦 pandas数据处理 1、删除重复元素 使用duplicated()函数检测重复的行，返回元素为布尔类型的Series对象，每个元素对应一行，如果该行不是第一次出现，则元素为True df.duplicated() 返回bool型的值,如果不重复返回false ,有重复值返回Ture 2. 映射 使用replace()函数，对values进行替换操作 1）replace还经常用来替换NaN元素 2) rename()函数：替换索引 3) map()函数：新建一列 transform()和map()类似 apply() agg() 3. 异常值检测 4. 排序 sort_values() sort_index() 5. 数据聚合【重点】 add_prefix()添加前缀 可以使用transform和apply实现相同功能 离散化和分箱 奥巴马VS罗姆尼 时间序列 重采样 大数据读取
Numpy中的argsort源码解析
Thomas_Cai的记忆殿堂
04-20 497
numpy的argsort排序算法，默认为快速排序模式，但其中是由三个算法组成的，分别为快速排序，插入排序以及堆排序，官方给的阈值为15，即需要排序的元素长度超过15则会进入快速排序。 快速排序的细节：前后循环到中间位置pm交换值使得pm前面的值小于pm对应值，后面的值大于pm对应的值，然后分为两部分，把元素较多部分放入栈中，利用栈来进行深度遍历。 之后，再进入插入排序，双指针往后退来排序。 最后，如果达成某个条件（NPY_UNLIKELY(cdepth < 0)）进入堆排序，这个还没看懂，至少我还进
NumPy 源码解析（四）
龙哥盟
07-05 948
strstr。
全方位剖析Numpy中的np.diag源代码
向往有那么一天梦幻的步态识别落地，开花❀！
08-02 817
全方位剖析Numpy中的np.diag源代码,Numpy中内置的函数diag是一个变化莫测的函数。
NumPy 源码解析（二十）
龙哥盟
07-05 332
.\numpy\numpy\f2py\tests\src\array_from_pyobj\wrapmodule.c /* * This file was auto-generated with f2py (version:2_1330) and hand edited by * Pearu for testing purposes. Do not edit this file unless you know what you * are doing!!! */ #ifdef __cpluspl
Python科学计算库Numpy数值运算基础详解（超详细 附源码）
showswoller的博客
01-05 1335
Python科学计算库Numpy数值运算基础详解（超详细 附源码）
解读一篇Numpy好文
算法channel
07-01 699
1最近工作太忙，每次回家洗洗就不想再开电脑码字了，写了也近两年了，习惯了，时间久了，不写都欲罢不能。尤其是有了好的点子，或者对某个概念或理论有了新的解读、新的展示形式、学...
NumPy Essentials 带注释源码 四、NumPy 核心和模块
热门推荐
龙哥盟
06-14 4万+
NumPy 核心和模块# 来源：NumPy Essentials ch4步长 # 步长是每个维度相邻两个元素的偏移差值 import numpy as npx = np.arange(8, dtype = np.int8) x # array([0, 1, 2, 3, 4, 5, 6, 7]) # x 是一维数组，步长为 1，因为 int8 占一个字节 x.strides # (1,) # data
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值