如何比较浮点数相等_【强基固本】算法工程师应该了解的浮点数知识

“强基固本，行稳致远”，科学研究离不开理论基础，人工智能学科更是需要数学、物理、神经科学等基础学科提供有力支撑，为了紧扣时代脉搏，我们推出“强基固本”专栏，讲解AI领域的基础知识，为你的科研学习提供助力，夯实理论基础，提升原始创新能力，敬请关注。

作者：知乎-Dounm

地址：https://www.zhihu.com/people/niu-chong

作为一个算法工程师，工作中经常会用到浮点数相关的知识，比如要对比两个浮点数的误差，再比如混合精度在 float 和 half 之间做变换。因此，有必要了解一些浮点数相关的知识。

01

浮点数的表示

根据国际标准IEEE 754，任意二进制浮点数都可表示为

•  ：符号位。  代表正数，  代表负数。

•  ：有效数字，大于1，小于2

•  ：指数位

举例：

•  的二进制是  ，则 

•  的二进制是  ，则 

•  的二进制是  ，则 

02

浮点数的存储

首先我们要注意区分浮点数的「表示值」(下标  )和「存储值」(下标  )。

上一节的例子中，  的值都是表示值，但真正把这些浮点数存储在内存中时，具体存储的值并不等同与表示的值。

这一些都是因为 IEEE 754 对  和  的存储还有些特殊规定。

针对有效数字 M

对于有效数字  ， IEEE 规定其表示值必须满足  ，所以  总是1.xxxxx的形式。

但 IEEE 规定存储  时可以不存第一位的1，所以  只保存xxxxx，即  ，这样就可以节省一位有效数字。

所以，前例中的  ，但实际只用存储  。

针对指数 E

对于指数E ，因为 E 是unsigned int，所以如果 E 有 8bit(Float)，那么取值为0~255；如果E 有11bit(Double)，取值为0~2047。

但科学计数法的 E 可以为负数，所以 IEEE 规定  。

对于8bit E (float)，Exponent Bias 是  ；对于11bit E (double)，Exponent Bias 是  。

因此，前例中  ，那如果用 Float 数据类型来保存该数字，真正要保存在内存里的其实是 

除此之外，还有两种特殊情况：

•  的 bits 全为0

以 float 数据类型为例，若按照默认规则，则  ；但实际上，对于此种情况，特殊规定  。

因此，  和  对应的  一样。但区别在于，  对应的有效数字的表示值  ，即 0.xxxxx(与默认规定不同)；而  对应的有效数字的表示值  1.xxxxx(与默认规定相同)。

为什么要对  采用特殊规定呢？
因为采用默认规定的话，我们能表示的最小数字  ，该num必然大于  。
而如果采用上述特殊规定，  ，则可以表示更小的数字，即 Subnormal Numbers。

•  的 bits 全为1
  如果此时  的 bits 全是0，则表示正负无穷大inf；否则就是NaN

03

总结

如果以存储值来表示任意浮点数的话(除去前面提到的两种特殊情况)，其默认公式如下：

常见浮点数据类型

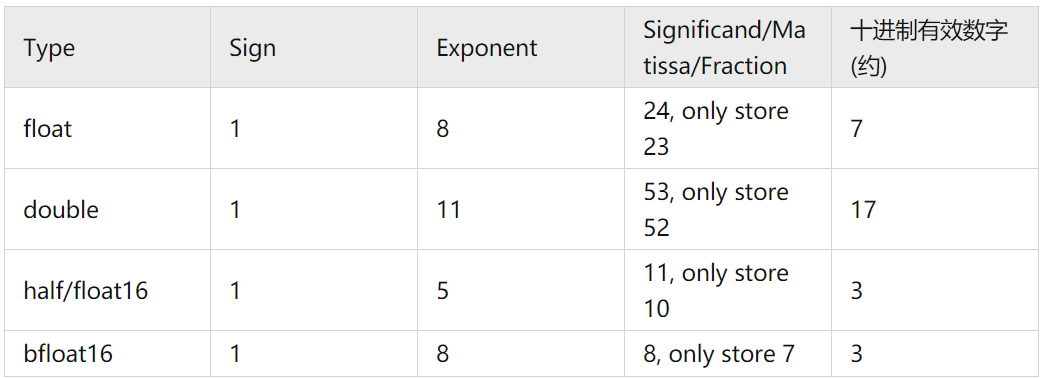
对于任意浮点数来说，其最高位存的是sign；最低位存储Fraction bit。

关于表格最右侧的十进制有效数字，因为  ，所以二进制精度如果是24位的话，那么十进制有效数字约7位。因此，对于 float16这种浮点数来说，其十进制有效数字就特别小，如果 debug 时看到两个 half 的区别特别大，也不用特别惊慌，这是正常现象 _(:3」∠)_

浮点数的一些其它相关

• 如果两个浮点数相加会怎样？

更小的数字会被shifted right来保证exponent一致，方便加法。因此，该更小的数字会损失部分的significand精度(即round-off error，Floating-point arithmetic - Wikipedia)

• 浮点数能否精确表示  ？

因为浮点数的存储也是基于二进制的，因此对于  这种无法用二进制精确表示的数字，实际上在计算机里存储的都是临近值(同理还有  等 )。

float a = 0.1;    cout << a << endl; // 输出0.1，因为cout的默认输出精度不高，所以会roundup为0.1cout.precision(10);   cout << a << endl; // 输出0.1000000015

• 如何判断两个浮点数相等？

因为浮点数会有精度损失，因此我们通常并不会用 == 来判断两个浮点数相等，而是判断两者 diff 是否足够小，小到一定程度就认为两个浮点数相等。

此处可以参考 numpy.isclose(...) 的实现，通过公式 absolute(a - b) <= (atol + rtol * absolute(b)) 来判断两个浮点数是否相等。

Refer

[1] IEEE 754-1985 - Wikipedia

https://en.wikipedia.org/wiki/IEEE_754-1985

[2] 浮点数的二进制表示

http://www.ruanyifeng.com/blog/2010/06/ieee_floating-point_representation.html

本文目的在于学术交流，并不代表本公众号赞同其观点或对其内容真实性负责，版权归原作者所有，如有侵权请告知删除。

直播预告

“强基固本”历史文章

• 神经网络量化简介

• 样本量极少如何机器学习？Few-Shot Learning概述

• 我们真的需要深度图神经网络吗？

• 深度强化学习(Deep Reinforcement Learning)入门

• 伪标签(Pseudo-Labelling)——锋利的匕首

• 基础算法：使用numpy实现逻辑回归随机梯度下降(附代码)

• 脉冲神经网络(SNN)

分享、点赞、在看，给个三连击呗！