首先从向量的乘法讲起,假设有个a向量和b向量,
那么这两个向量的点积或者乘积可以写为
希望你对上面这行还有印象。对于向量的意义,如果你要探究几何意义的话,我觉的只有当a或者b是单位向量的时候才有意义,就是所谓的投影。向量的诞生是来解决实际问题的,用来解决的最直接的一个问题是力的做功:
下面我们开始讨论一下函数,首先试想一下,函数是什么?函数的定义域是不是可以看做是向量坐标中的维度 i ,而值域就是向量每个坐标对应的值,也就是说函数可以看成一个维度无限大的向量。假设有个两个函数
函数向量的乘积就是常说的函数点积,可以写为:
现在应该理解,从-inf 到 +inf 的积分不过是一个两个函数向量的点积而已。函数点积的意义是什么呢,可以完全从向量点积的意义照搬啊,就是变力变位移的做功啊,就是做功啊做功啊Work啊。</





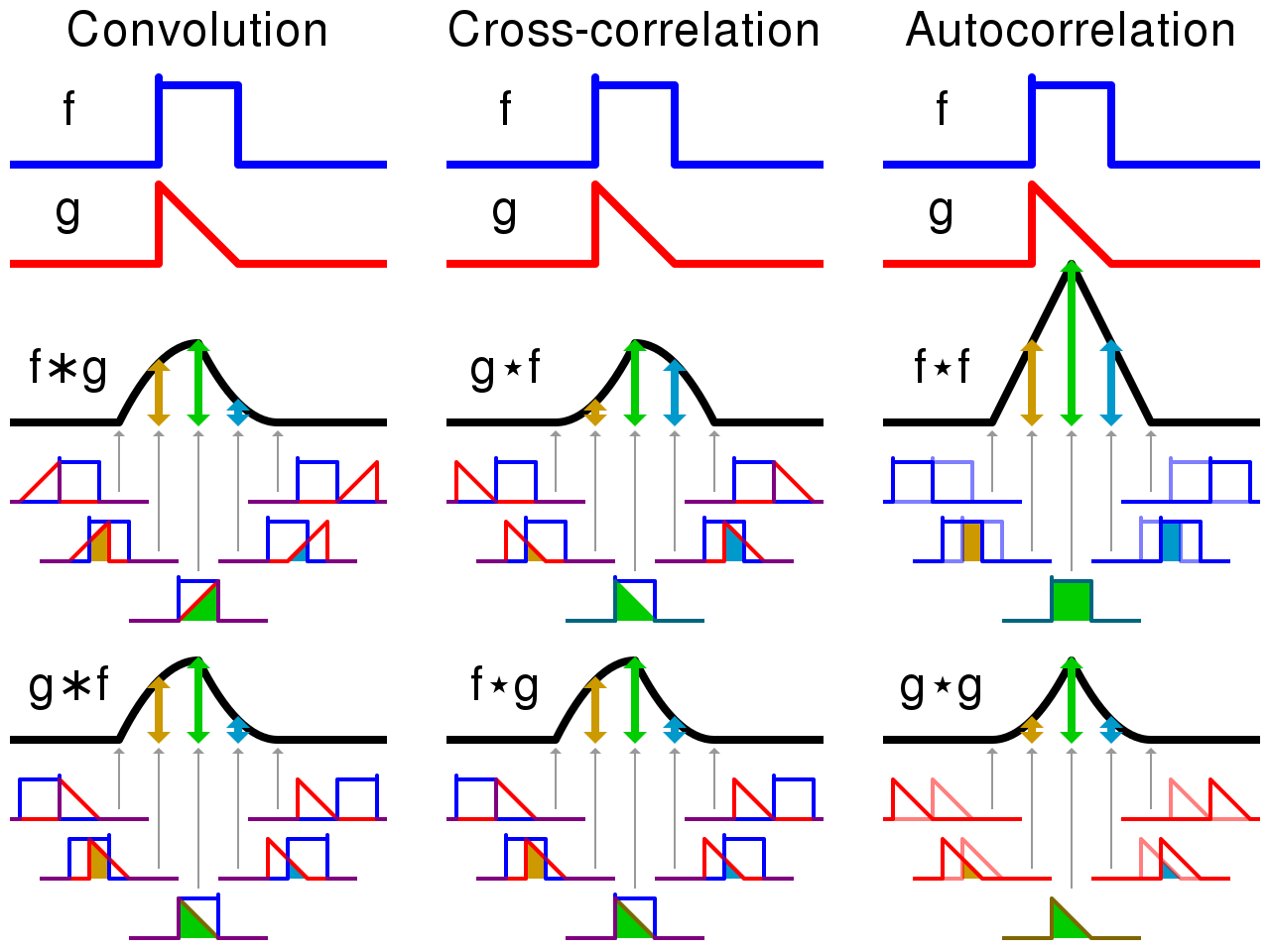
 本文从向量乘法的角度引入,解释了函数的乘积与积分的几何意义,进而阐述了卷积、互相关和自相关的概念。通过信号与系统中的例子,详细解析了卷积的过程,强调了卷积在时间轴上的平移特性。同时,介绍了互相关和自相关的应用,如迈克尔逊干涉仪和AGWN,并提供了卷积、互相关和自相关的比较图,帮助读者深入理解这些概念。
本文从向量乘法的角度引入,解释了函数的乘积与积分的几何意义,进而阐述了卷积、互相关和自相关的概念。通过信号与系统中的例子,详细解析了卷积的过程,强调了卷积在时间轴上的平移特性。同时,介绍了互相关和自相关的应用,如迈克尔逊干涉仪和AGWN,并提供了卷积、互相关和自相关的比较图,帮助读者深入理解这些概念。
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章

















 7594
7594

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








