深度学习：卷积（Convolution）详解

摘要：本文系统讲解卷积运算的核心概念，包括卷积步长（Stride）、三维卷积以及其在图像处理中的实际应用，帮助理解 CNN 的基础原理。

---

一、什么是卷积？

卷积（Convolution）是卷积神经网络（CNN）中最基本的操作，用于：

✅ 提取图像的局部特征，如边缘、纹理、形状等。

🌐 类比理解：

• 就像用一个小窗口在图片上滑动，每次只看一小块区域；
• 在 AI 中，这个“小窗口”就是过滤器（Filter），也叫卷积核（Kernel）。

---

二、卷积步长（Stride）

🔍 定义：

卷积步长（Stride）是指过滤器在输入图像上每次移动的像素数。

✅ 默认情况：步长 = 1

• 过滤器每次向右或向下移动一个元素；
• 每个位置都会被计算一次。

✅ 步长 = 2

• 过滤器每次跳过一个元素；
• 输出矩阵尺寸更小，计算更快。

---

📌 示例：7×7 图像 + 3×3 过滤器 + 步长 = 2

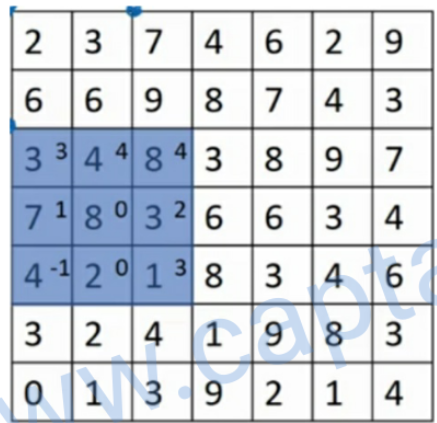
🔄 卷积过程（步长=2）：

• 第一次：左上角开始 → 得到输出第一个元素（91）
• 第二次：向右移动 2 格 → 得到第二个元素（100），如果说剩余的部分不足以完成卷积则不执行
• 向下移动 2 行，重复

✅ 输出矩阵（3×3）：

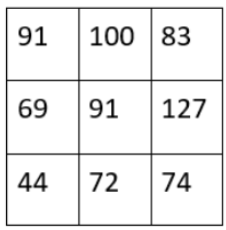
⚠️ 注意：由于步长大于 1，部分位置被跳过，因此输出尺寸变小。

---

三、输出维度公式（含步长与 Padding）

其中：

• ( n )：输入尺寸
• ( p )：Padding 大小
• ( f )：过滤器尺寸
• ( s )：卷积步长
• ( )：向下取整

✅ 示例：

• 输入：7×7
• 过滤器：3×3
• Padding：0
• 步长：2

✅ 输出为 3×3 矩阵。

---

四、三维卷积：处理彩色图像

🎨 彩色图像的表示

• 黑白图：二维矩阵（H × W）
• 彩色图：三维张量（H × W × C），C 表示通道数（通常为 3：R, G, B）

例如：6×6×3 的 RGB 图像

---

🔧 三维卷积操作

为了处理彩色图像，过滤器也必须是三维的，维度为：

例如：

• 输入：6×6×3
• 过滤器：3×3×3
• 输出：4×4×1（单通道）

---

🧪 三维卷积过程详解

1. 逐层相乘：

   

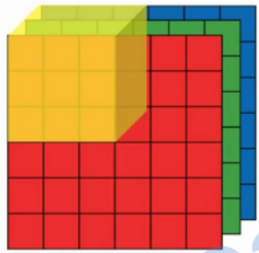
   • 过滤器第 1 层（红色）与输入第 1 层（红色）对应元素相乘；
   • 过滤器第 2 层（绿色）与输入第 2 层（绿色）相乘；
   • 过滤器第 3 层（蓝色）与输入第 3 层（蓝色）相乘；

2. 累加求和：

   • 将所有 3 层的乘积结果相加，得到输出的一个值。

✅ 总共进行 27 次乘法（3×3×3），然后求和。

---

五、如何选择过滤器参数？

目标	建议
检测红色边缘	设置过滤器中绿色、蓝色层全为 0
检测绿色边缘	设置红色、蓝色层全为 0
检测所有颜色边缘	所有层都启用

💡 例如：若只想检测红色边缘，则将过滤器的第 2、3 层设为 0。

---

六、总结

🔑 卷积是计算机视觉的基石 —— 它让模型能够从局部信息中学习全局结构。

对于开发者而言，掌握卷积意味着：

1. 理解 CNN 的工作原理；
2. 能够设计合适的过滤器和超参数；
3. 为后续的池化、激活函数、残差连接打下基础。