拟牛顿法matlab程序_牛顿环实验的数据处理改进及图像分析

牛顿环是光的一种薄膜干涉图样，最早是由牛顿于1675年首先观察得到的，当用单色光照射牛顿环装置时，在视觉上为一系列明暗相间的同心圆环。 这些圆圈的距离不同，随着到中心点的距离增加而逐渐变窄，它们是由球面上与平面上反射的光线相互干涉而形成的干涉条纹。 以往实验室通常使用的逐差法处理实验数据，过程较为繁杂，其计算结果也不够准确。 在牛顿环实验中获得的某组数据通过逐差法计算牛顿环透镜曲率，其相对扩展不确定度为0.82%，由于“逐差”先两两相减使得自由度减半，即重复测量或组合测量时计算实验标准偏差所用的独立残差个数减半，未能充分利用测得的有效数据信息，这不符合实验设计随机化原则的思路。 本文通过线性拟合法处理实验数据，并利用GUI建立一个可进行数值分析以及图像动态分析的交互式界面，不仅可以得到更精确的实验结果，其相对扩展不确定度为0.65%，还能结合实际选择牛顿环实验参量以观察到不同的实验现象，简便易行，应用范围广。

1 牛顿环实验理论

牛顿环装置如图1所示，牛顿环干涉的明暗条纹条件满足：

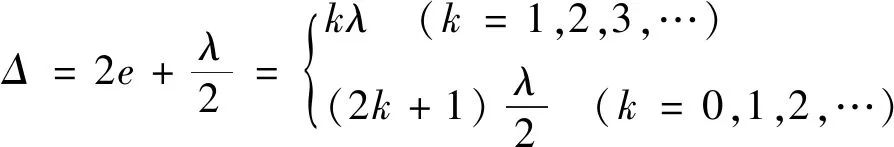
得到牛顿环暗纹公式[1]

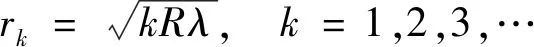
由于单色光的波长λ已知，测量得到第k级的暗环半径，可以计算得到牛顿环凸透镜的曲率半径。由于中心切点处的压力形变或残留粉尘作用，实际方程式由上式修正为

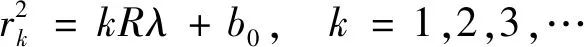
(1)

b0指的是由于凸透镜中心切点处的压力形变或残留粉尘作用，使得牛顿环的暗环公式不再是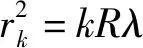这样的正比例关系，而是需要在右边加上一个常数，这个常数反映的是压力形变或残留粉尘作用所带来的影响，即b0。

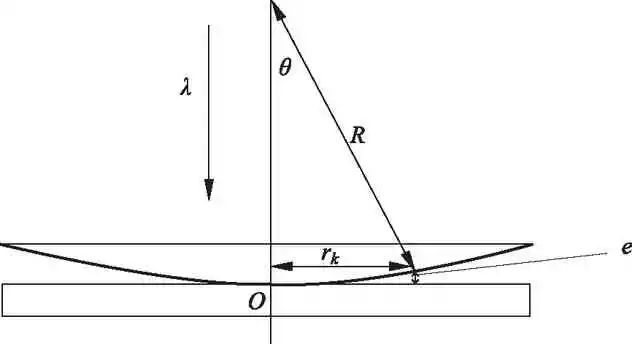
图1 牛顿环装置示意图e指的是牛顿环装置中的凸透镜和底面平板之间的厚度距离

2 传统实验数据处理方法——逐差法

考虑到凸透镜和平面镜表面的尘埃和凹陷，以及波长误差、平晶不平度、部分余弦(投影)误差、被测面偏离理想球面等误差使得显微镜观察下的牛顿环中心将会是一个圆斑。于是改为测量牛顿环的各暗环直径即可避免这种误差。若求得了第m级及第n级的暗环直径Dm,Dn，记m-n=25即可得到计算公式：

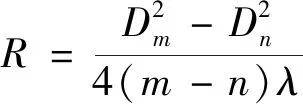
(2)

此时已知单色光源为钠光灯，其波长λ=589.3nm，通过逐差法即可计算得到曲率半径R。具体的逐差法计算结果见表2所示。(其中XL,XR分别表示某暗环中心在牛顿环左侧和右侧的位置)

表1 牛顿环各级暗环半径位置记录表

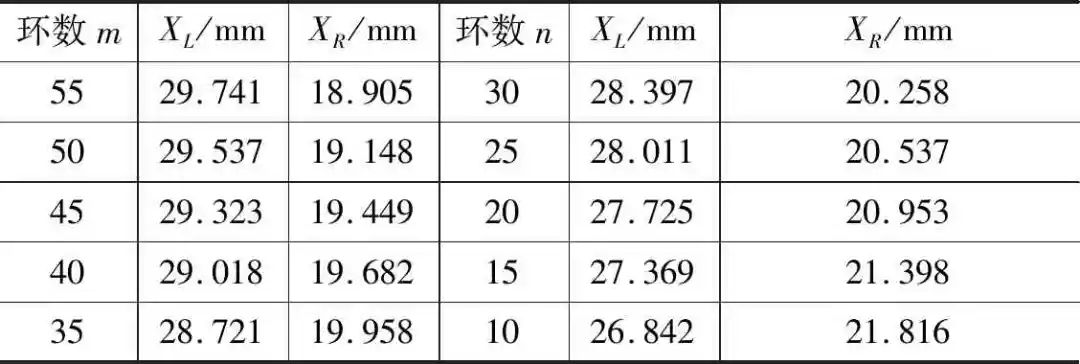
表2 逐差法处理数据结果

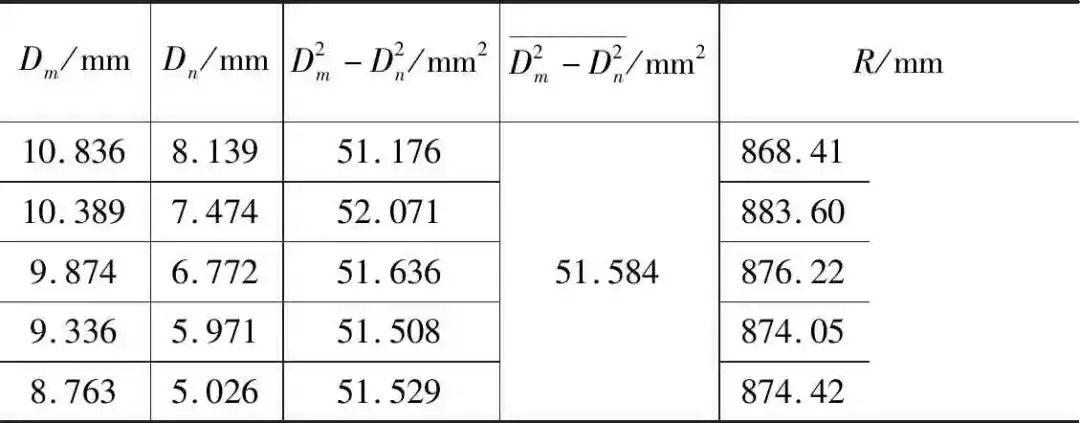
将数据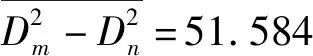代入式(2)，计算透镜曲率半径值为：R=875.34mm。

测量结果的B类不确定度主要由两个分量组成，即仪器误差限和瞄准误差限。因变量