泊松分布记为_统计分布理论 常见分布总结

• bernoulli distribution

1. 定义：一个非常简单的试验是只有两个可能结果的试验. 结果1的概率是p，结果2的概率是1-p.
2. μ=p
3. σ^2=p(1-p)

• binomial distribution

1. 定义：n重伯努利试验成功次数的离散概率分布. 每次伯努利试验的成功概率为p，X代表成功的次数，则X的概率分布是二项分布，记为X~B(n,p).
2. μ=np
3. σ^2=np(1-p)

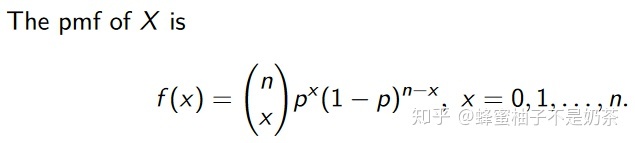
• geometric distribution

1. 定义：在n次伯努利试验中，试验第k次才得到第一次成功的机率。一次实验中成功的概率是p.
2. μ=1/p
3. σ^2=q/(p^2)

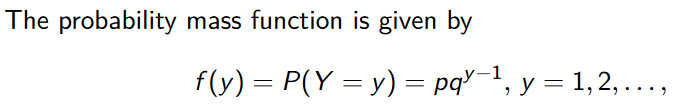
• negative binomial distribution

1. 定义：负二项分布是统计学上一种离散概率分布。满足以下条件的称为负二项分布：实验包含一系列独立的实验， 每个实验都有成功、失败两种结果，成功的概率是恒定的，实验持续到r次不成功，r为正整数. (不同资料对于r和k的定义是不同的，要根据解释走，这里我们和百度百科一致).
2. μ=rp/1-p

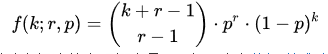
• poisson distribution

1. 定义：泊松分布适合于描述单位时间内随机事件发生的次数。
2. μ=λ
3. σ^2=λ

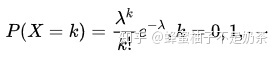
5.limiting binomial for p small and n large→poisson distribution

• uniform distribution

1. 定义：均匀分布由两个参数a和b定义，它们是数轴上的最小值和最大值，通常缩写为U(a,b).

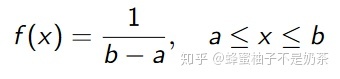
3.

• exponential distribution

1. 定义：指数分布（也称为负指数分布）是描述泊松过程中的事件之间的时间的概率分布，即事件以恒定平均速率连续且独立地发生的过程。 这是伽马分布的一个特殊情况。 它是几何分布的连续模拟，它具有无记忆的关键性质。 除了用于分析泊松过程外，还可以在其他各种环境中找到。
2. μ=θ
3. σ^2=θ^2
4. 有时候用来判断指数分布

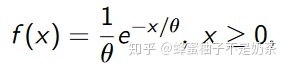
• gamma distribution

2.

3.μ=αθ

4.σ^2=αθ^2

• chi-square distribution

1. μ=αθ=r
2. σ^2=αθ^2=2r
3. Let X has a gamma distribution with θ=2 and α=r/2, where r is a positive integer. The pdf of X is then：

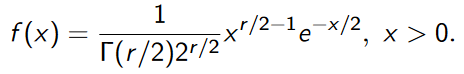
• normal distribution

1. standardization of the normal distribution：if X is N(μ,σ^2), then Z=(X-μ)/σ is N(0,1).