主成分分析
- 一个非监督的机器学习算法
- 主要用于数据的降维
- 通过降维,可以发现更便于人类理解的特征
- 其他应用:可视化,去噪
对数据进行简化的一系列原因:
- 使得数据集更易使用
- 降低很多算法的计算开销
- 去除噪声
- 使得结果易懂
什么是主成分分析?
在PCA中,数据从原来的坐标系转换到了新的坐标系,新的坐标系的选择是由数据本身决定的。第一个新坐标轴选择的是原始数据中方差最大的方向,第二个新坐标轴的选择和第一个坐标轴正交且具有最大方差的方向。该过程一直重复,重复次数为原始数据中特征的数目,我们会发现,大部分方差都包含在最前面的几个新坐标轴中。因此,可以忽略余下的坐标轴,及对数据进行了降维处理。
PCA优缺点
- 优点:降低数据的复杂性,识别最重要的多个特征
- 缺点:不一定需要,且可能损失有用信息
- 使用数据类型:数值型数据
举个例子理解一下,二维空间上有一些样本点如下,将二维降维至一维:
| 原始样本点(二维) | 映射到特征1上 | 映射到特征2上 |
 |  |  |
从图中可以看到,将样本点映射到特征1这种方案感觉会好一些,因为相较另一种方案,样本与样本之间的间距较大一些,也就是说点和点之间的区分度更大一些。那有没有更好地映射方案呢?来看看下面这中映射成一维的方案:
| 原始样本点(二维) | 找一根直线 | 将所有的点都映射到这根直线上 |
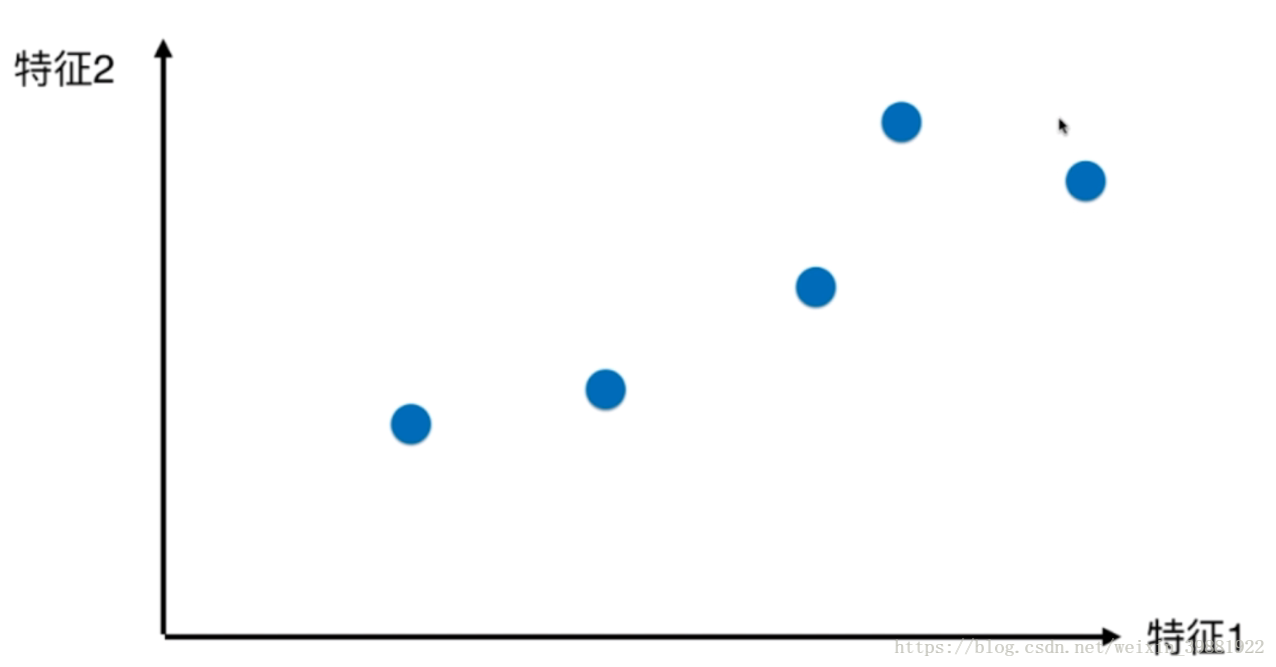 | 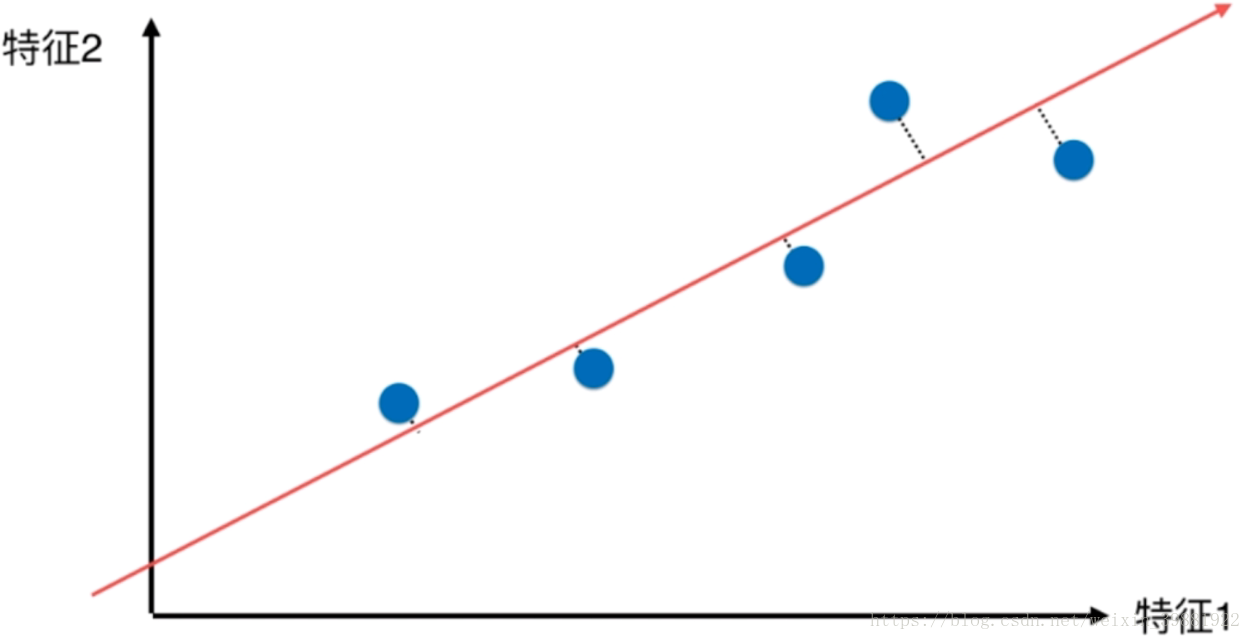 | 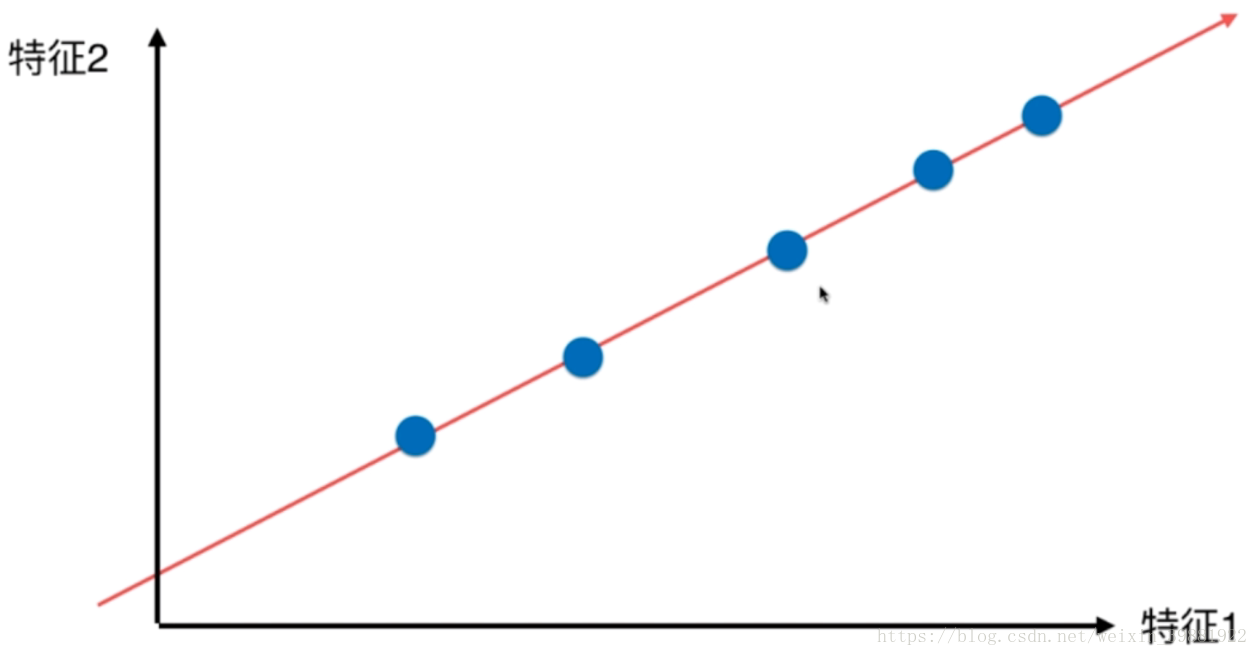 |
在这种映射方案下,我们可以看到它将所有的点都映射到直线上,虽然线是斜的,我们也可以把它看成是一个轴,一个维度,可以看到所有的点在映射之后,可以发现它们与原来的样本点的分布并没有更大的差距,并且样本之间的距离(可区分度)也比无论映射到x轴还是y轴都要大。
那么我们需要思考的就是如何找到这个让样本间间距最大的轴?如何定义样本间的间距?通常情况下,我们使用方差(Variance),因为方差可以作为反映样本的疏密的一个指标。
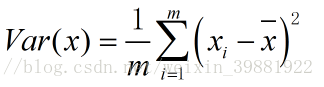
这样上面的降维问题,就转化成为了找到一个轴,使得样本空间的所有点映射到这个轴后,方差最大的问题。
为了解决这个问题,在进行主成分分析之前,要做一些工作:
第一步:将样例的均值归为0(demean),所有样本减去整体的均值,可以看到处理之后,样本分布没有改变,只是坐标轴变了。
| 原始样本分布 | demean之后 |
 | 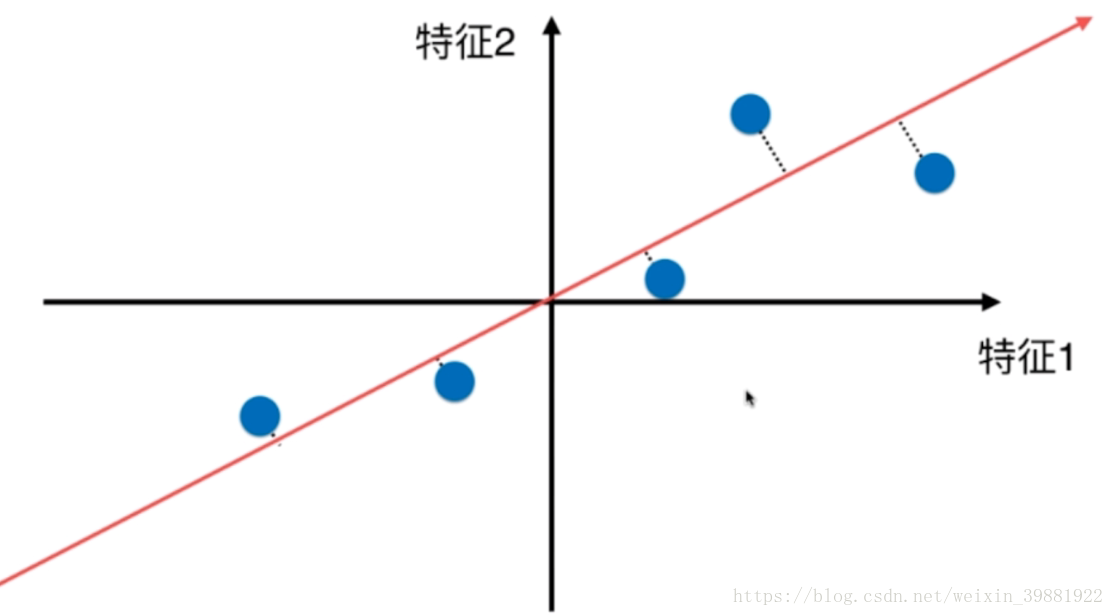 |
demean之后样本均值为0,方差公式就可以做出一些改变,更加方便
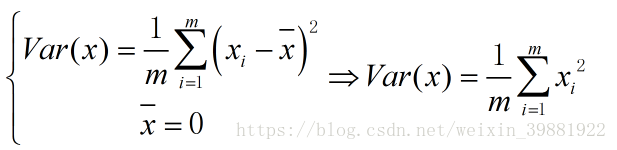
第二步,求这个轴的方向w=(w1,w2)(两维的表达),使得我们所有的样本映射到w维度上方差最大,即
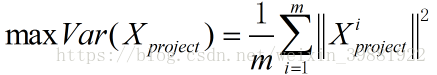
| 图解 | |
w为要映射的轴的方向,蓝色的点为原始的样本点,映射到w上,其实就是蓝色的那跟线段,其实也就是点乘的定义
| 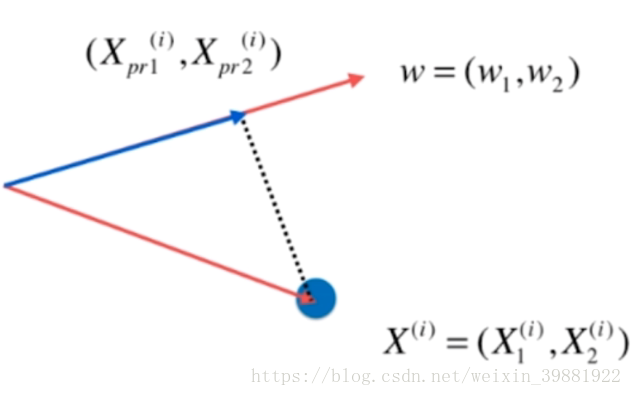 |
由这个问题,扩展到N维,主成分分析的目标就是求w,使得映射到此维度后,方差最大

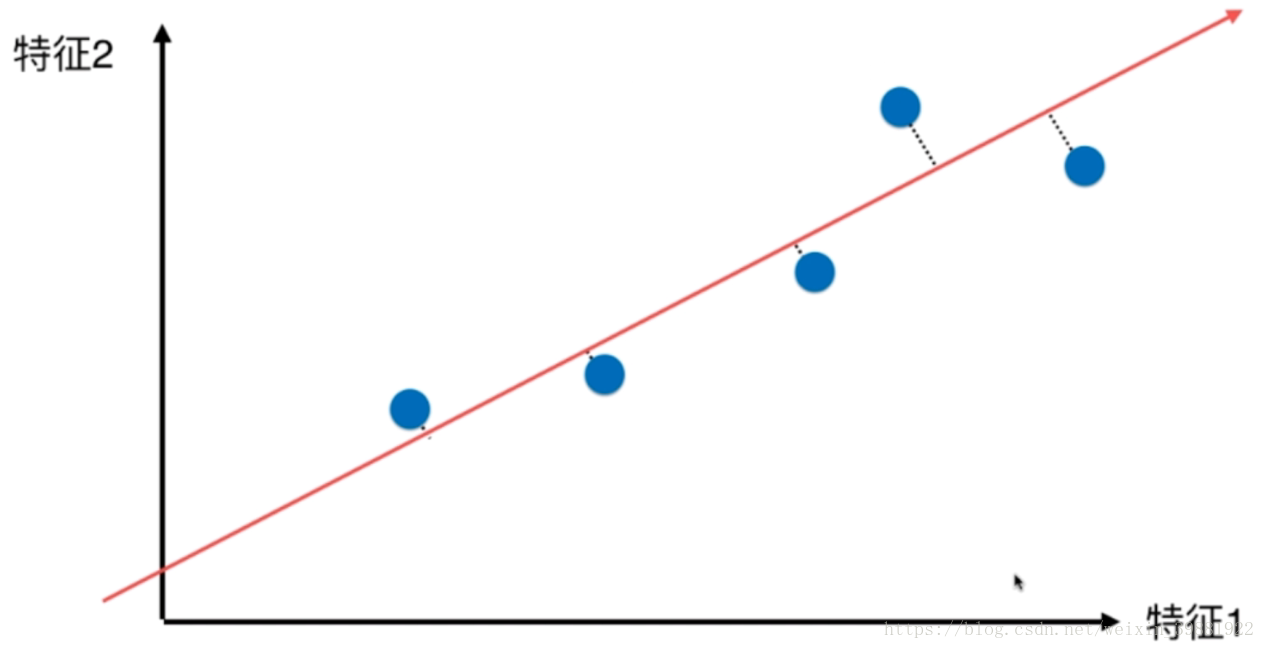
插曲,光看图我们会感觉到pca和线性回归有些相似,但需要注意他们之间的差别
| PCA | 线性回归 |
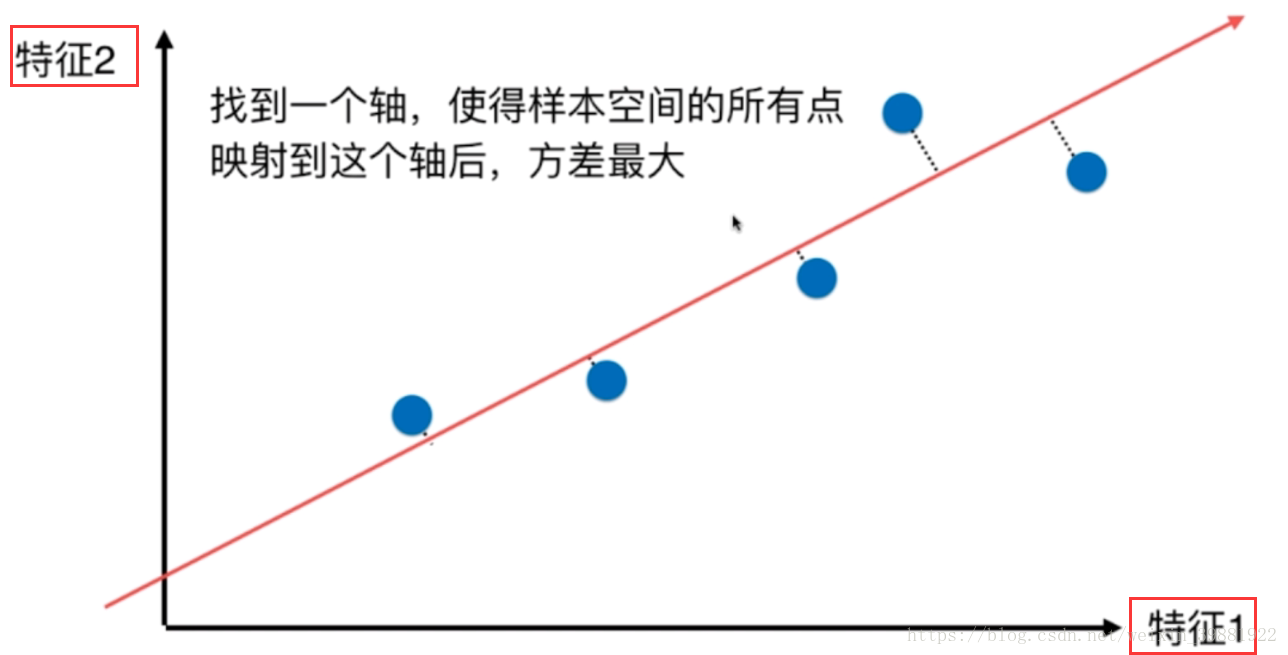 | 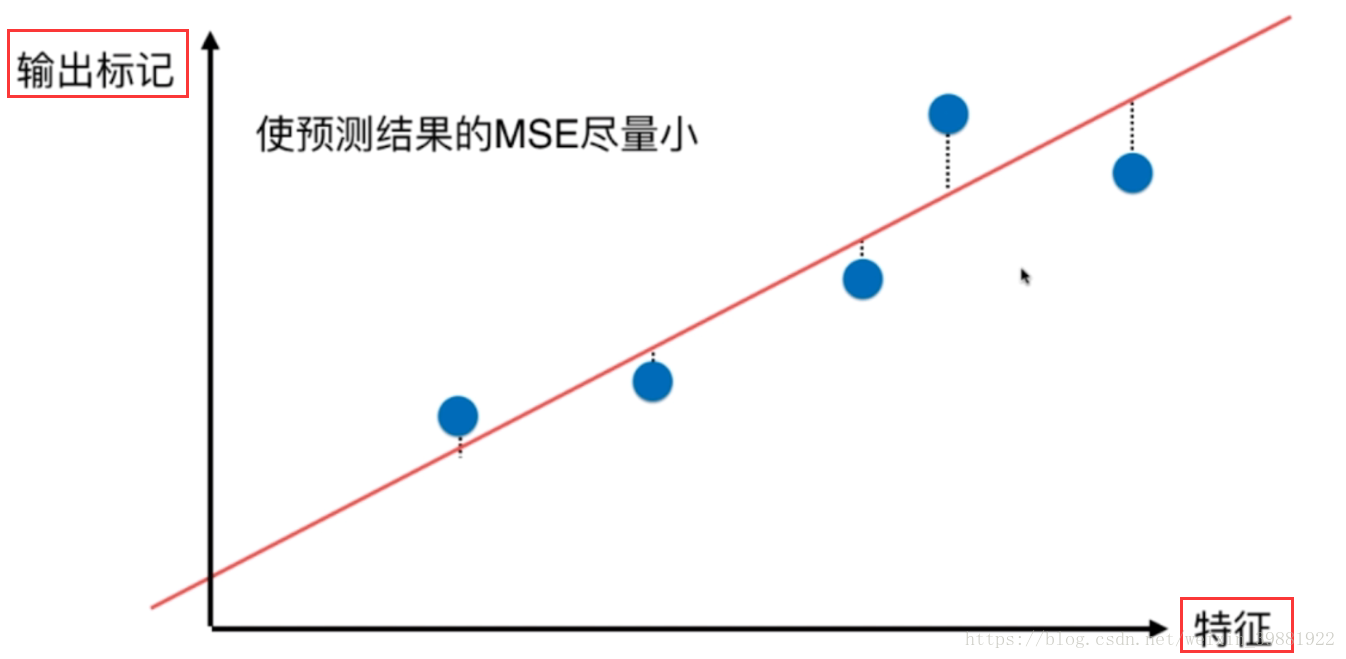 |
横轴轴是特征 推导式子不同 虽然都是样本与一条直线的关系,但pca是距离时点垂直于直线 | 横轴特征,纵轴输出标记 推导式子不同 点垂直于特征 |
梯度上升法解决主成分分析问题

1.生成数据,进行demean
import numpy as np
import matplotlib.pyplot as plt
X=np.empty(shape=(100,2))
#从一个均匀分布[low,high)中随机采样,注意定义域是左闭右开,即包含low,不包含high.
X[:,0]=np.random.uniform(1,100,size=100)
X[:,1]=0.75*X[:,0]+3+np.random.normal(0,10,size=100)
plt.scatter(X[:,0],X[:,1])
plt.title('X')
plt.show()
def demean(X):
#求每列的均值,也是每个特征维度上的均值
return X-np.mean(X,axis=0)
X_demean=demean(X)
plt.scatter(X_demean[:,0],X_demean[:,1])
plt.title('demean(X)')
plt.show()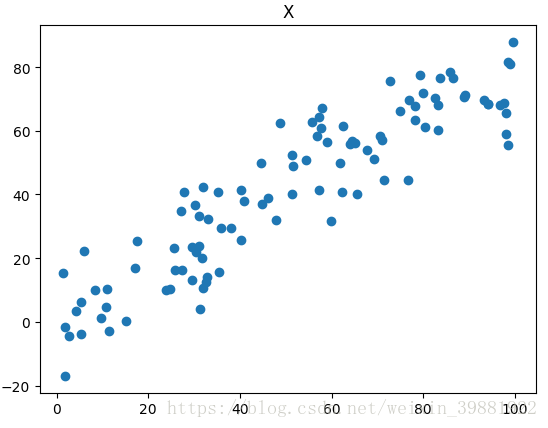 | 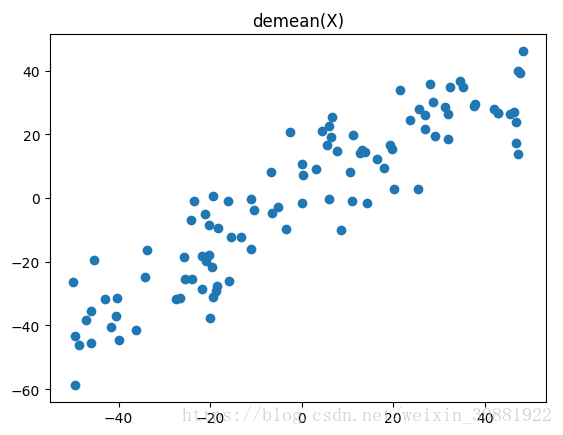 |
2.梯度上升法
def f(w,X):
'''
目标函数
:param w:映射向量
:param X: 样本数据
:return:
'''
return np.sum(np.dot(X,w)**2)/len(X)
def df(w,X):
'''
目标函数求梯度
:param w:
:param X:
:return:
'''
return 2/len(X)*np.dot(X.T,np.dot(X,w))
def direction(w):
'''
将向量w转化为单位向量
:param w:
:return:
'''
return w/np.linalg.norm(w)
def gradient_ascent(df,X,init_w,eta,max_iters=1e4,epsilon=1e-8):
'''
梯度上升
:param df:
:param X:
:param init_w:
:param eta: 步长学习率
:param max_iters: 最大迭代步数
:param epsilon: 精度
:return:
'''
cur_iter=0
w=direction(init_w)
while cur_iter<max_iters:
gradient=df(w,X)
last_w=w
w=w+eta*gradient
w=direction(w)
if(abs(f(w,X)-f(last_w,X))<epsilon):
break
cur_iter+=1
return w
init_w=np.random.random(X.shape[1])
eta=0.01
w=gradient_ascent(df,X,init_w,eta)
plt.scatter(X_demean[:,0],X_demean[:,1])
plt.plot([-50,w[0]*80],[-50,w[1]*80],c='r')
plt.title('demean(X)')
plt.show()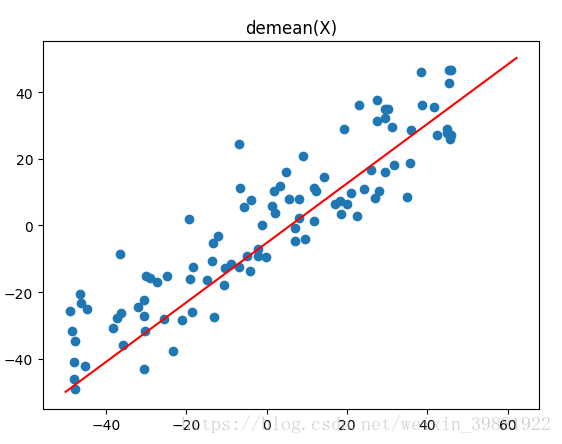
将数据进行改变,将数据在第一个主成分上的分量去掉,即下图中的X',然后在新的数据上求第一主成分
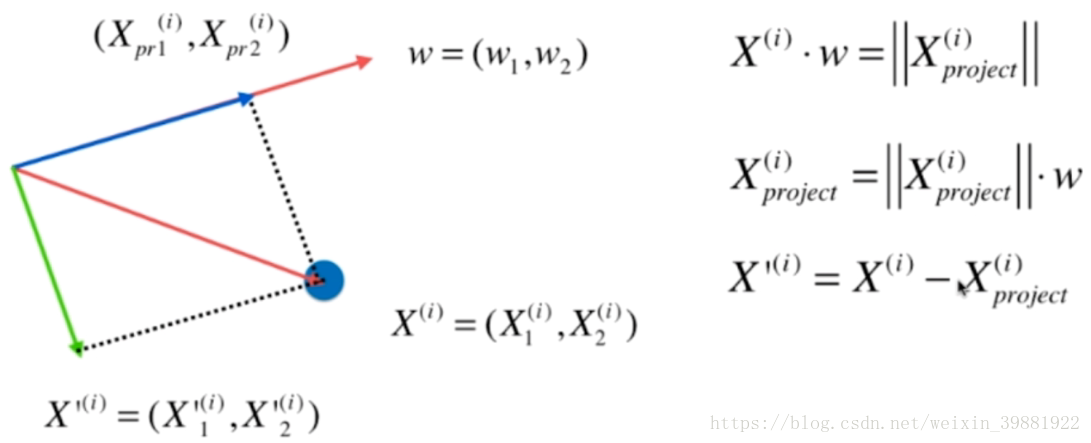
# X2=np.empty(X.shape)
# for i in range(len(X)):
# X2[i]=X[i]-np.dot(X[i],w)*w
X2=X-np.dot(X,w).reshape(-1,1)*w
plt.scatter(X2[:,0],X2[:,1])
plt.title('X2')
plt.show()
w2=gradient_ascent(df,X2,init_w,eta)
print(w2)
#垂直应该等于0
print(w.dot(w2))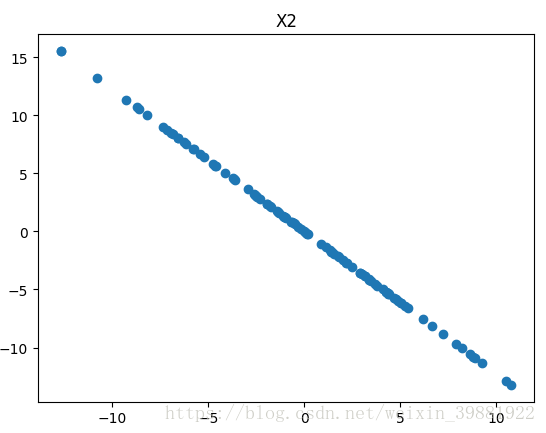
def first_n_components(n,X,eta=0.01,n_iter=1e4,epsilon=1e-8):
x_pca=X.copy()
x_pca=demean(x_pca)
res=[]
for i in range(n):
init_w=np.random.random(x_pca.shape[1])
w=gradient_ascent(df,x_pca,init_w,eta)
res.append(w)
x_pca=x_pca-np.dot(x_pca,w).reshape(-1,1)*w
return res
print(first_n_components(2,X))[array([ 0.75823566, 0.65198059]), array([ 0.65198379, -0.7582329 ])]高维数据向低维数据映射
| 样本数据(m行n列) | X的前k个主成分(k行,n列) |
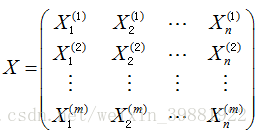 |
|
将高维数据向低维数据映射,其实就是求
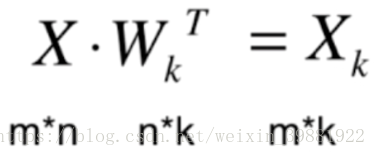
反之,从低维映射到高维也是可以的
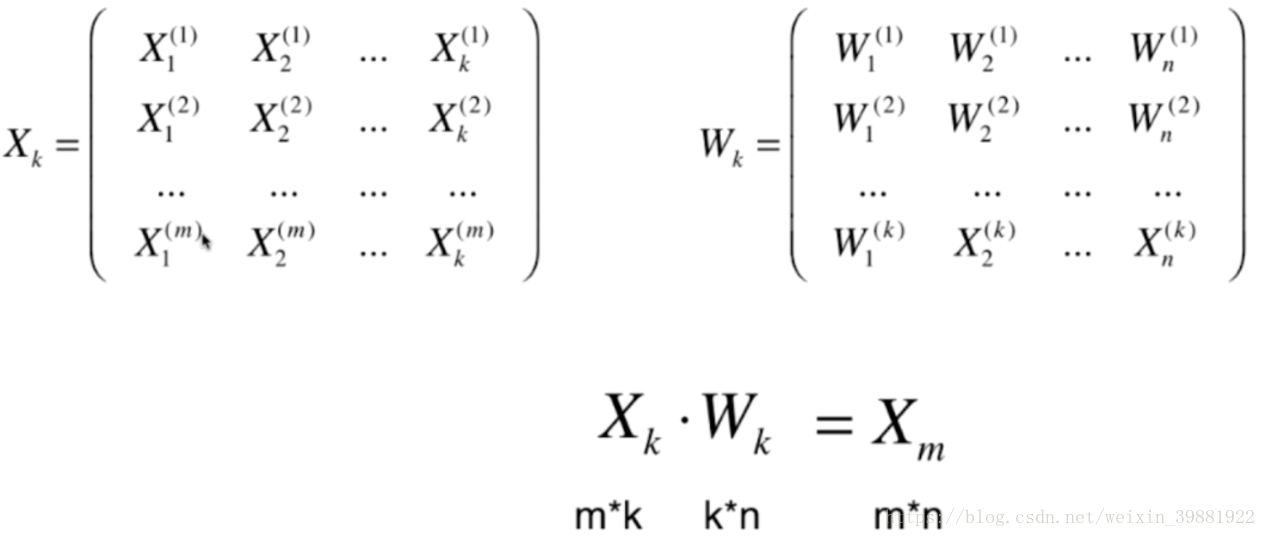
import numpy as np
class PCA:
def __init__(self,n_components):
'''
:param n_components: 指定几个主成分
'''
self.n_components=n_components
self.components_=None
def __repr__(self):
return 'pca%d个主成分'%self.n_components
def fit(self,X,eta=0.01,n_iter=1e4):
'''根据训练数据集X获得数据的均值和方差'''
def demean(X):
# 求每列的均值,也是每个特征维度上的均值
return X - np.mean(X, axis=0)
def f(w, X):
'''
目标函数
:param w:映射向量
:param X: 样本数据
:return:
'''
return np.sum(X.dot(w) ** 2) / len(X)
def df(w, X):
'''
目标函数求梯度
:param w:
:param X:
:return:
'''
return 2 / len(X) * np.dot(X.T, np.dot(X, w))
def direction(w):
'''
将向量w转化为单位向量
:param w:
:return:
'''
return w / np.linalg.norm(w)
def gradient_ascent(df, X, init_w, eta=eta, max_iters=n_iter, epsilon=1e-8):
'''
梯度上升
:param df:
:param X:
:param init_w:
:param eta: 步长学习率
:param max_iters: 最大迭代步数
:param epsilon: 精度
:return:
'''
w = direction(init_w)
cur_iter = 0
while cur_iter < max_iters:
gradient = df(w, X)
last_w = w
w = w + eta * gradient
w = direction(w)
if (abs(f(w, X) - f(last_w, X)) < epsilon):
break
cur_iter += 1
return w
x_pca=demean(X)
self.components_=np.empty(shape=(self.n_components,X.shape[1]))
for i in range(self.n_components):
init_w=np.random.random(x_pca.shape[1])
w=gradient_ascent(df,x_pca,init_w)
self.components_[i,:]=w
x_pca=x_pca-np.dot(x_pca,w).reshape(-1,1)*w
return self
def transform(self,X):
'''将给定的X,映射到各个主成分分量中'''
return np.dot(X,np.transpose(self.components_))
def inverse_transform(self,X):
'''将给定的X,反向映射回原来的特征空间'''
return np.dot(X,self.components_)
import matplotlib.pyplot as plt
X=np.empty(shape=(100,2))
#从一个均匀分布[low,high)中随机采样,注意定义域是左闭右开,即包含low,不包含high.
X[:,0]=np.random.uniform(1,100,size=100)
X[:,1]=0.75*X[:,0]+3+np.random.normal(0,10,size=100)
pca=PCA(n_components=2)
pca.fit(X)
print(np.transpose(pca.components_))
#降维
pca=PCA(n_components=1)
pca.fit(X)
x_reduction=pca.transform(X)
print(x_reduction.shape)
#恢复原始维度
x_restore=pca.inverse_transform(x_reduction)
print(x_restore.shape)
plt.scatter(X[:,0],X[:,1],c='b')
plt.scatter(x_restore[:,0],x_restore[:,1],c='g')
plt.show()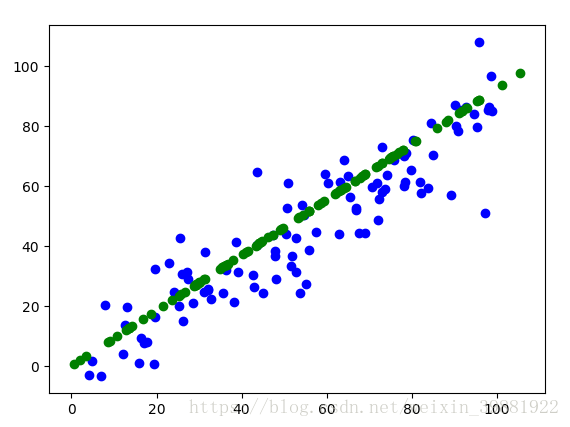
SKlearn中的PCA
import numpy as np
import matplotlib.pyplot as plt
X=np.empty(shape=(100,2))
#从一个均匀分布[low,high)中随机采样,注意定义域是左闭右开,即包含low,不包含high.
X[:,0]=np.random.uniform(1,100,size=100)
X[:,1]=0.75*X[:,0]+3+np.random.normal(0,10,size=100)
from sklearn.decomposition import PCA
pca=PCA(n_components=1)
pca.fit(X)
print(pca)
print(pca.components_)
x_reduction=pca.transform(X)
print(x_reduction.shape)
x_restore=pca.inverse_transform(x_reduction)
plt.scatter(X[:,0],X[:,1],c='b')
plt.scatter(x_restore[:,0],x_restore[:,1],c='g')
plt.show()import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
digits=datasets.load_digits()
x=digits.data
y=digits.target
from sklearn.model_selection import train_test_split
x_train,x_test,y_train,y_test=train_test_split(x,y,random_state=666)
print(x_train.shape)
from sklearn.neighbors import KNeighborsClassifier
knn_clf=KNeighborsClassifier()
knn_clf.fit(x_train,y_train)
print(knn_clf.score(x_test,y_test))
from sklearn.decomposition import PCA
pca=PCA(n_components=2)
pca.fit(x_train)
x_train_reduction=pca.transform(x_train)
x_test_reduction=pca.transform(x_test)
knn_clf=KNeighborsClassifier()
knn_clf.fit(x_train_reduction,y_train)
print(knn_clf.score(x_test_reduction,y_test))
#解释各轴方差相应的比例
print(pca.explained_variance_ratio_)
pca=PCA(n_components=64)
pca.fit(x_train)
print(pca.explained_variance_ratio_)
plt.plot([i for i in range(64)],[np.sum(pca.explained_variance_ratio_[:i+1]) for i in range(64)])
plt.show()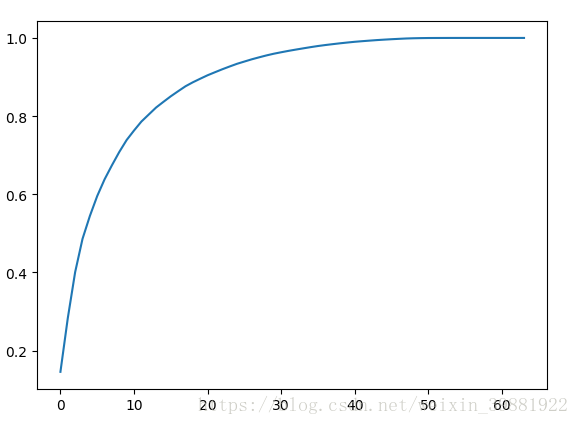
pca=PCA(0.95)
pca.fit(x_train)
print(pca.n_components_)
x_train_reduction=pca.transform(x_train)
x_test_reduction=pca.transform(x_test)
knn_clf=KNeighborsClassifier()
knn_clf.fit(x_train_reduction,y_train)
print(knn_clf.score(x_test_reduction,y_test))
#降到2维进行可视化
pca=PCA(n_components=2)
pca.fit(x)
x_reduction=pca.transform(x)
for i in range(10):
plt.scatter(x_reduction[y==i,0],x_reduction[y==i,1],alpha=0.5)
plt.show()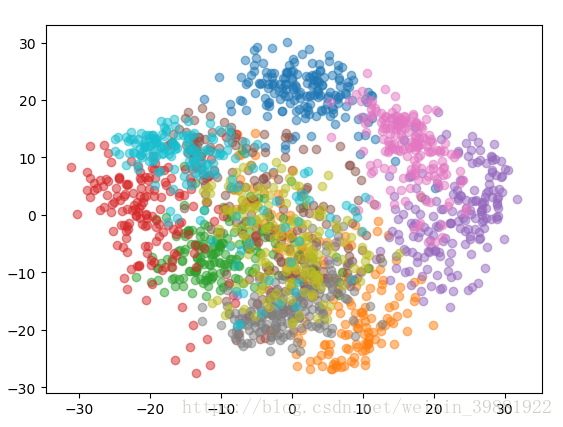
PCA+MNIST
import numpy as np
from sklearn.datasets import fetch_mldata
mnist=fetch_mldata("MNIST original",data_home='./mnist')
print(mnist)
x=mnist['data']
y=mnist['target']
x_train=np.array(x[:60000],dtype=float)
y_train=np.array(y[:60000],dtype=float)
x_test=np.array(x[60000:],dtype=float)
y_test=np.array(y[60000:],dtype=float)
from sklearn.neighbors import KNeighborsClassifier
knn_clf=KNeighborsClassifier()
knn_clf.fit(x_train,y_train)
print(knn_clf.score(x_test,y_test))
#pca降维
from sklearn.decomposition import PCA
pca=PCA(0.9)
pca.fit(x_train)
x_train_reduction=pca.transform(x_train)
knn_clf.fit(x_train_reduction,y_train)
x_test_reduction=pca.transform(x_test)
print(knn_clf.score(x_test_reduction,y_test)){'COL_NAMES': ['label', 'data'], 'data': array([[0, 0, 0, ..., 0, 0, 0],
[0, 0, 0, ..., 0, 0, 0],
[0, 0, 0, ..., 0, 0, 0],
...,
[0, 0, 0, ..., 0, 0, 0],
[0, 0, 0, ..., 0, 0, 0],
[0, 0, 0, ..., 0, 0, 0]], dtype=uint8), 'target': array([ 0., 0., 0., ..., 9., 9., 9.]), 'DESCR': 'mldata.org dataset: mnist-original'}
0.9688
0.9728可以看到在降维之后,不仅节省了计算开销,正确率也上升了,一箭双雕。
使用PCA对数据进行降噪
import numpy as np
from sklearn import datasets
import matplotlib.pyplot as plt
digits=datasets.load_digits()
x=digits.data
y=digits.target
#生成噪声数据
noise_digits=x+np.random.normal(0,4,size=x.shape)
#y=0的数字10个
example_digits=noise_digits[y==0,:][:10]
print(example_digits.shape)
#将另外的1-9标签各类图片10张,压入example_digits中
for num in range(1,10):
x_num=noise_digits[y==num,:][:10]
example_digits=np.vstack([example_digits,x_num])
print(example_digits.shape)
#画图
def plot_digits(data,title):
fig,axes=plt.subplots(10,10,figsize=(10,10),
subplot_kw={'xticks':[],'yticks':[]},gridspec_kw=dict(hspace=0.1,wspace=0.1))
for i,ax in enumerate(axes.flat):
ax.imshow(data[i].reshape(8,8),
cmap='binary',
interpolation='nearest',
clim=(0,16))
plt.title(title)
plt.show()
plot_digits(example_digits,'降噪前')
#因为噪声较多,只选取50%的信息
from sklearn.decomposition import PCA
pca=PCA(0.5)
pca.fit(noise_digits)
print(pca.n_components_)
components=pca.transform(example_digits)
filtered_digits=pca.inverse_transform(components)
plot_digits(filtered_digits,'降噪后')| 降噪前 | 降噪后 |
 |  |
import numpy as np
from sklearn.datasets import fetch_lfw_people
import matplotlib.pyplot as plt
faces=fetch_lfw_people()
#对所有的样本进行一个随机的排列
random_indexes=np.random.permutation(len(faces.data))
x=faces.data[random_indexes]
example_faces=x[:36,:]
print(example_faces.shape)
def plot_faces(data):
fig,axes=plt.subplots(6,6,figsize=(10,10),
subplot_kw={'xticks':[],'yticks':[]},gridspec_kw=dict(hspace=0.1,wspace=0.1))
for i,ax in enumerate(axes.flat):
#图片w*h=62,47
ax.imshow(data[i].reshape(62,47))
plt.show()
plot_faces(example_faces)
from sklearn.decomposition import PCA
pca=PCA(svd_solver='randomized')
pca.fit(x)
plot_faces(pca.components_[:36,:])| 降维前 | 降维后 |
 | 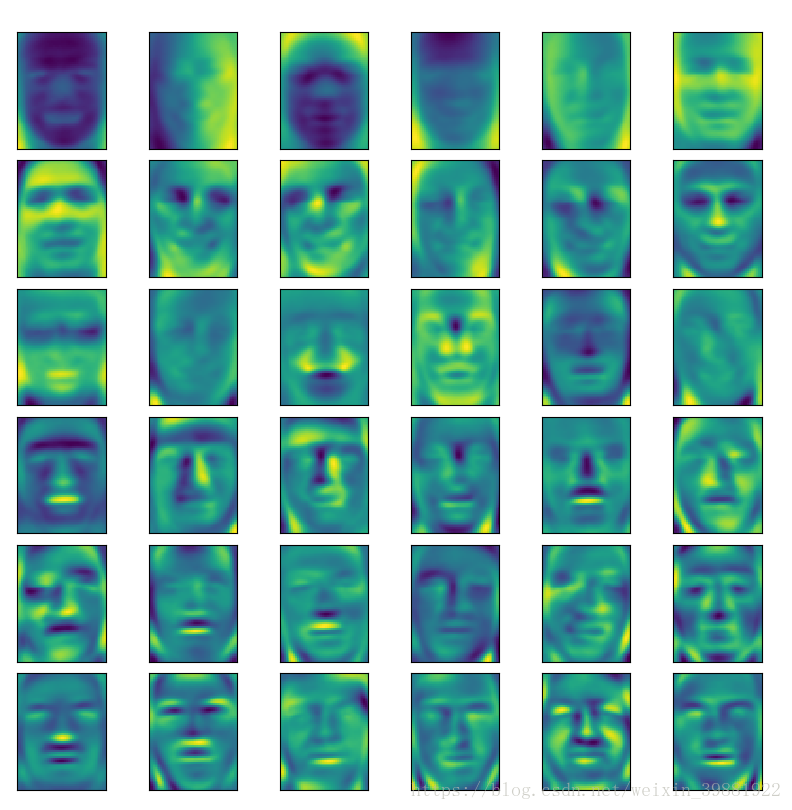 |










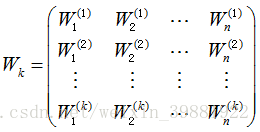
















 46万+
46万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








