LARS再探之交叉验证- 零基础python机器学习笔记-第四天

上一篇初探中我们只是简单的看了下LARS的一个运算过程没有区分训练集和测试集，这里我们再加上交叉验证。
1. 简介交叉验证
之前我一直都是用sklearn.model_selection中的train_test_split函数自动随机划分训练集和测试集。之所以出现交叉验证，主要是因为训练集较小，在实际情况下，人们不是很喜欢用交叉验证，因为它会耗费较多的计算资源。
但是如果超参数数量越多，我们就需要越大的验证集，如果验证集的数量不够，那么就需要使用交叉验证了。一般都是分成3、5和10折。

以5折交叉验证为例，

• fold1-fold4作为训练集用来训练模型，学习参数；
• fold5作为验证集并不参与学习参数的确定，也就是验证集并没有参与梯度下降的过程，只是为了选择超参数；
• test data做为测试集只使用一次，即在训练完成后评价最终的模型时使用，它既不参与学习参数过程，也不参数超参数选择过程，而仅仅使用于模型的评价。
  **值得注意的是测试集在训练过程中是不可以出现的！不然模型就相当于“作弊”看到答案了。

2. 代码看LARS交叉验证过程
注：这里的代码没有另外先找出测试集，只是模拟了10折交叉验证中训练集和验证集拟合出最优模型的过程。

import pandas as pd
import matplotlib.pyplot as plt
import numpy as np

#读取数据
target_url = "https://archive.ics.uci.edu/ml/machine-learning-databases/undocumented/connectionist-bench/sonar/sonar.all-data"
#其中header和prefix的作用为在没有列标题时指定列名
df = pd.read_csv(target_url, header=None, prefix='V')

df['V60'] = df.iloc[:,-1].apply(lambda v:1.0 if v== 'M' else 0.0)

# 数据标准化  并拆分成属性x和标签y
norm_df = (df - df.mean())/df.std()
xData = norm_df.values[:,:-1]; yData = norm_df.values[:,-1] 

# 设置 步数 和 步长
nSteps = 500; stepSize = 0.001
# 设置 交叉验证折数
nxval = 10

errors = np.array([0.0]*nSteps)
errorList = []

MseList = np.array([0.0]*nxval)

for ixval in range(nxval):
    idxs = range(len(yData))
    idxTest = [i for i in idxs if i % nxval == ixval % nxval]
    idxTrain = [i for i in idxs if i % nxval != ixval % nxval]
    test_X = xData[idxTest,:]; test_y = yData[idxTest]
    train_X = xData[idxTrain,:]; train_y = yData[idxTrain]
    
    # 回归系数\beta向量初始化
    beta = np.array([0.0]*train_X.shape[1])
    
    for i in range(nSteps):
        #计算残差
        resid = train_y - train_X.dot(beta)
        
        #计算属性与残差相关性
        corr = resid.dot(train_X)
        
        #找出最大相关性的属性， 并更新其beta值
        idx = np.abs(corr).argmax()
        corrMax = corr[idx]
        
        beta[idx] += stepSize * corrMax / abs(corrMax)
        
        # 填充测试集偏差矩阵（步数 * (nxval*测试集样本数)）
        err = test_y - test_X.dot(beta)
        errors[i] = np.dot(err,err)/len(err)
      
      #这里1和297是先算出来后写上为了看最优模型beta值的  
        if ixval==1 and i==297:
            print(beta)
            print(pd.value_counts(beta))
        
    errorList.append(list(errors))
    
    minStep = np.argmin(errors)
    minMse = errors[minStep]
    
    MseList[ixval] = minMse
    
#最优模型对应的交叉验证 验证集折数
minval = np.argmin(MseList)
minerror = errorList[minval]
#最优模型对应的步数
minStep = np.argmin(minerror)
minMse = minerror[minStep]

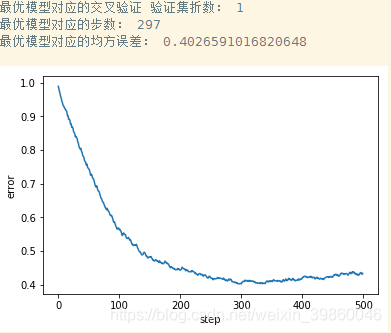
print ("最优模型对应的交叉验证 验证集折数：", minval)
print ("最优模型对应的步数：", minStep)
print ("最优模型对应的均方误差：", minMse)

# 绘制交叉验证的均方误差曲线
plt.plot(minerror)
plt.xlabel("step")
plt.ylabel("error")
plt.show()

3. 结果分析
最优模型为：

最佳模型对应的参数beta为：