蒙特卡洛分析_马尔可夫链蒙特卡洛方法MCMC

大多数时候，贝叶斯统计在结果在最好的情况下是魔法，在最糟糕时是一种完全主观的废话。在用到贝叶斯方法的理论体系中，马尔可夫链蒙特卡洛方法尤其神秘。这篇文章将介绍马尔可夫链蒙特卡洛方法，及其背后的基本数学推理。

关键词：马尔可夫链蒙特卡洛方法MCMC

本期内容转载自：Ben Shaver

---

首先，什么是马尔可夫链蒙特卡洛(MCMC)方法呢？最简单的回答就是：“MCMC就是一种通过在概率空间中采样来近似感兴趣参数的后验分布的方法”。

一、贝叶斯理论体系基础术语

感兴趣的参数只是用来抽象我们感兴趣的现象的一些数字。通常我们会使用统计的方法来估计这些参数。例如，如果我们想了解成年人的身高，那么我们需要的参数可能就是以英寸为单位的平均身高。

分布就是参数的各个可能值和我们能观察到每个参数的可能性的数学表示。最好的例子就是钟形曲线：

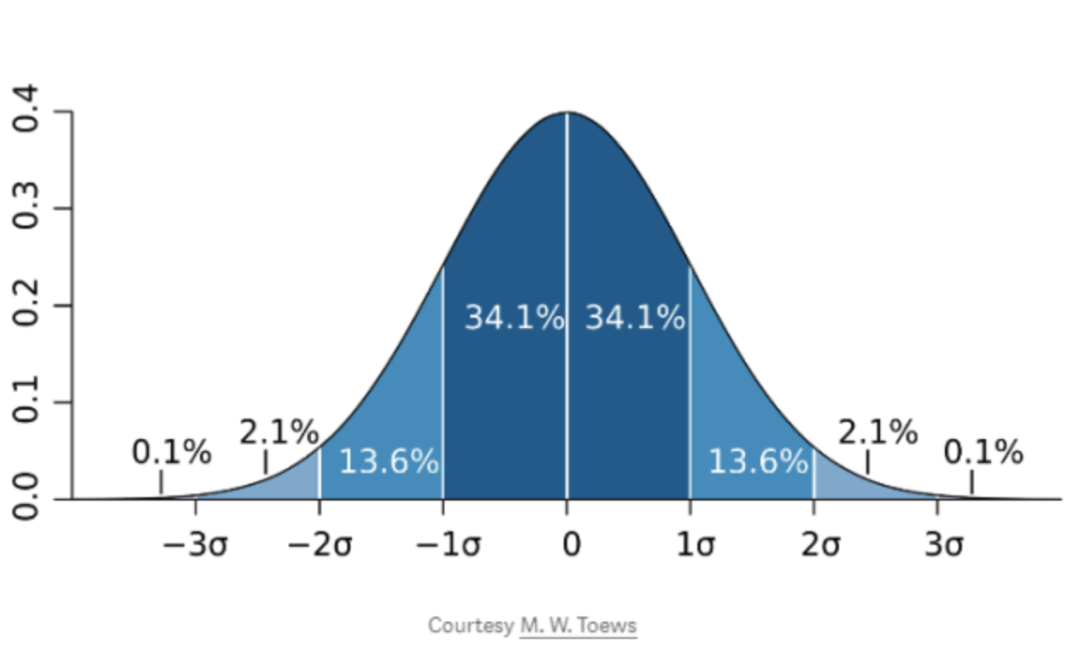
在贝叶斯统计方式中，分布还有另一个解释。贝叶斯不仅仅代表参数的值和每个参数的真实值有多大，而是认为分布描述了我们对参数的确信度。因此，上面的钟形曲线可以表明我们非常确定参数的值接近于零，同时我们认为真实值高于或低于该值的可能性是相等的。事实上，人的身高是遵循一个正态分布的，所以我们假设平均人体高度的真实值遵循如下的钟形曲线：

显然，这个图表表示这个人群以巨人的身高生活了很多年，因为据调查所知，最有可能的平均身高是6'2”英寸。

让我们想象某人去收集了一下些数据，然后他们观察到了一批5英寸到6英寸之间的人。我们可能用另一个正态分布曲线来表示这些数据，这个曲线显示了哪个人体平均身高值最能解释数据：