并查集基础

以下为个人理解，如果有不同想法欢迎应评论交流。

首先说概念，实际上就是将将同类型的元素合并为一个集合并可以进行查找，就是实现分类，那么最重要的操作就是合并和查找了。

接下来我们先讨论一下集合的逻辑结构该如何处理呢？这里举个例子，此例子以下讨论都会用到。

[0,1][0,2][1,2][3,4]数组中的元素两辆相关，就是说0与1有关，0与2有关，1与2有关，3与4有关。那么我们是不是可以把0，1，2放在一个集合中，3，4放在一个集合中。首先我们先来用图的方式描述他们的关联，这里以为没有说明具体关系以及是否具有方向性，故我们使用无向图的方式进行描述。如图

这样就描述了两个集合，但是我们发现对于第一个集合来说有些关系是冗余的，我们只是想描述他们在一个集合内，并不想关心它们谁跟谁是有关系的，所以我们并不需要这么复杂的关系，要尽量将其简化但又要保持连通，故我们将其用最小连通图存储他们之间的关系。（若对图这里的概念不是很了解的话可以去看一下）最小连通图也就是构成一棵树。如图（这里注意最小连通图不止一种，这里只是其中一种），

那我们就以树的形式存储。下面贴出代码，

数组A用于描述这些元素的集合分类，故初始化时每一个元素都自成一个集合。

之前我们总结说以树的形式存储这个集合，那么必然就会有父子关系，而查找的作用就是要查找到该节点的根节点（注意是根节点不是父节点，这一点从递归的形式就可以看出）。

这里我们写的合并集合是将y作为x的根使得两个集合合并起来，当然两者的关系可以调换。我们来用以上代码模拟一遍刚刚的例子。

初始化：A[]的初始状态为0 1 2 3 4。而他们之间的关系为[0,1][0,2][1,2][3,4]。

调用tree_union()  传入参数[0,1]过后A[]的存储为1 1 2 3 4。建立起来的逻辑关系为

调用tree_union()  传入参数[0,2]过后A[]的存储为1 2 2 3 4。建立起来的逻辑关系为

调用tree_union()  传入参数[1,2]过后A[]的存储为1 2 2 3 4。建立起来的逻辑关系为

调用tree_union()  传入参数[3,4]过后A[]的存储为1 2 2 4 4。建立起来的逻辑关系为

这样集合就分好了，那么如何去确定是否属于一个集合呢？通过find（）函数查到根是谁就是属于那个集合。

但是问题来了，像这样的存储方法数据多了是不是就会形成一长串度为1的树，那么对于查找路径来说时间复杂度就会大大增加。所以我们应该使用压缩路径的方法，那么我们应该满足的条件为，①最小连通图。②树的高度尽量小（高度小了自然查找路径就短）。那么我们应该从逻辑上做的变化为如图，

如此一来，压缩路径就完成了。那么代码上肯定是需要有改变的。

这一步变化主要是保证每一个节点都是其根的子节点（与根的路径为1）。

同时注意还解决了之前代码的一个死循环问题，例如对之前代码调用tree_union()  传入参数[0,2]，[2,0]过后A[]的存储为2 1 0 3 4

那么在调用find函数时就会陷入死循环。

这一步改变主要是改变合并方式。试想一下我们之前的代码的以两个集合的形式合并的方式为

那么改变之后就会是

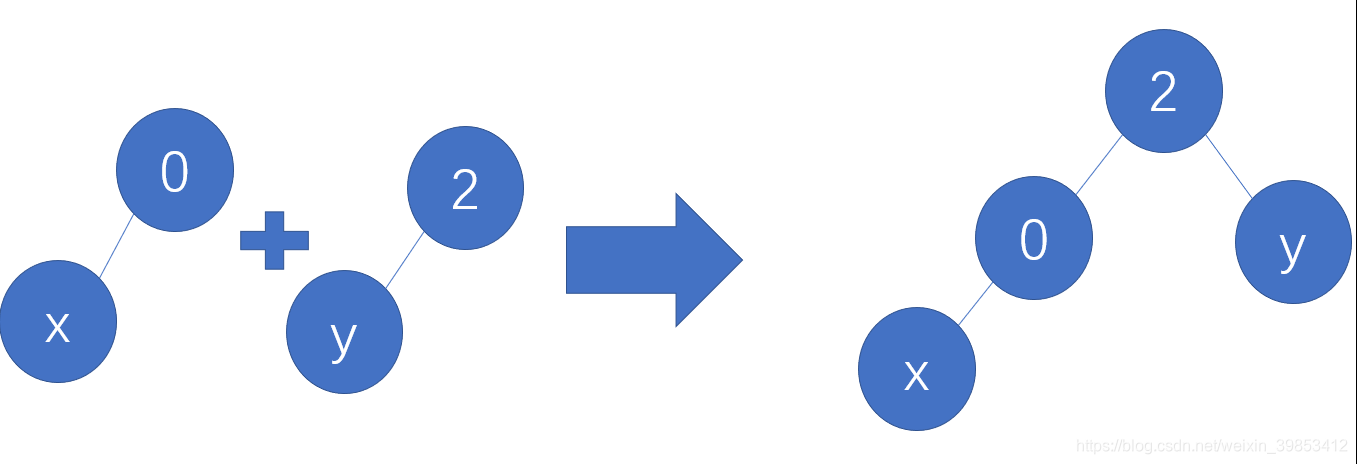
故我们使用并查集还是要用压缩路径的方法。