自动控制原理第七版胡寿松pdf_自动控制原理简明笔记—(05)

这里是一则小广告：

关注作者请点击这里哦：zdr0

我的专栏里面不仅有学习笔记，也有一些科普文章，相信我的专栏不会让您失望哦～大家可以关注一下：数学及自然科学

-尽力写最好的讲义，尽力写最好的科普。

---

二阶系统的时域分析

二阶系统是以二阶微分方程作为运动方程的控制系统。在控制工程中，不仅二阶系统的典型应用极为普遍，而且不少高阶系统的特性在一定条件下可用二阶系统的特性来表征。因此，着重研究二阶系统的分析和计算方法具有较大的实际意义。大家也要稳扎稳打，扎实的掌握二阶系统及其特性。

二阶系统的时域模型

对于一个二阶系统，其标准闭环传递函数的形式为：

其对应的微分方程是：

其中：

• ：
  自然频率；
• ：
  阻尼比。

相对应的结构图如图片3.3所示：

图片3.3：标准形式的二阶系统结构图。

令式

中的分母多项式为零，则可以得到

二阶系统的特征方程为：

其两个根称为闭环极点，为：

显然，二阶系统的时间相应取决于

和

这两个参数。应当指出的是，对于结构和功用不同的二阶系统，

和

的物理含义是不同的。

二阶系统的单位阶跃响应

在闭环极点中，若

，则二阶系统具有两个正实部的特征根，其单位阶跃响应为：

其中：

。

由于阻尼比

为负，指数因子具有正幂指数，因此系统的动态过程为发散的正弦振荡或单调发散的形式，从而表明

的二阶系统是不稳定的。

• 如果
  ，则特征方程有一对纯虚根，
  ，对应于
  平面虚轴上一对共轭极点，可以计算出系统的阶跃响应为等幅振荡，此时，系统相当于没有阻尼的情况；
• 如果
  ，则特征方程有一对具有负实部的共轭复根，
  ,对应于
  平面左半部的共轭复数极点，响应的阶跃响应为衰减的振荡过程，此时系统处于欠阻尼的状态；
• 如果
  则特征方程具有两个相等的负实根，
  ，对应于
  平面负实轴上两个相等的实极点，相应的阶跃响应非周期地趋于稳态输出，此时系统处于临界阻尼的情况；
• 如果
  ，则特征方程有两个不相等的负实根
  ，对应于
  平面上两个不相等的实极点，相应的阶跃响应也是非周期地趋于稳态输出，但响应速度比临界阻尼情况缓慢，因此成为过阻尼的情况。

上述各种闭环极点在

平面上的分布情况如图片3.4所示。

图片3.4：二阶系统的闭环极点分布。

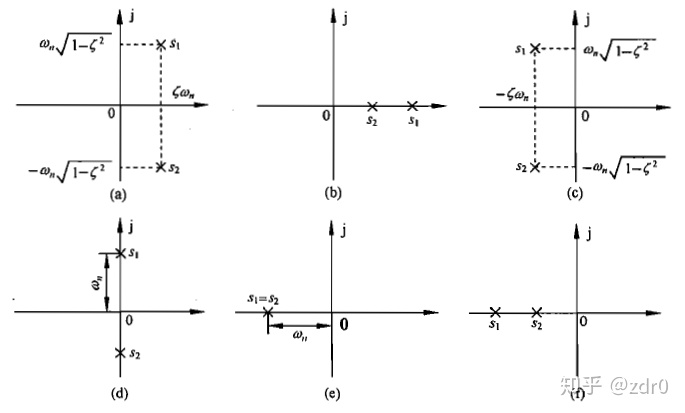
由此可见，

值的大小决定了系统的阻尼程度。下面，我们将分别研究欠阻尼、临界阻尼、过阻尼二阶系统的单位阶跃响应。

欠阻尼

二阶系统的单位阶跃响应

若令

则有：

其中，

称为

衰减系数，

称为

阻尼振荡频率。

当

时，由式

可得：

对式

取逆

变化可得：

其中，

。

式

表明，欠阻尼二阶系统的单位阶跃响应由两部分组成：稳态分量为

；瞬态分量为阻尼正弦振荡项，其振动频率为

，故称为阻尼振荡频率。由于瞬态分量衰减的快慢程度取决于包络线

收敛的速度，当

一定时，包络线的收敛速度有取决于指数函数

的幂，所以，

称为衰减系数。

若

，则二阶系统在无阻尼的情况下的单位阶跃响应为：

的值由系统本身的结构参数决定，常称为

自然频率。

临界阻尼

二阶系统的单位阶跃响应

设输入信号为单位阶跃函数，则系统输出量的

变化可以写为：

对式

取逆

变换，得到临界阻尼二阶系统的单位阶跃响应为：

式

表明，当

时，二阶系统的单位阶跃响应应为稳态值为

的无超调的上升过程，其变化率为：

当

时，响应的变化率为零，当

时，相应过程的变化率为正，响应过程单调递增，当

时，响应的变化率趋于零，响应过程趋近于常值

。通常，临界阻尼情况下的二阶系统的单位阶跃响应称为临界阻尼响应。

过阻尼

二阶系统的单位阶跃响应

令：

则过阻尼二阶系统的输出量的

变换为：

式中，

称为过阻尼二阶系统的时间常数，且有

。对上式取逆

变化得到：

式

表明，响应特性包含着两个单调递减的指数项，其代数和绝不会超过稳态值

，因而过阻尼二阶系统的单位阶跃响应是非振荡的，通常称为过阻尼响应。

欠阻尼二阶系统的动态过程分析

在控制工程中，除了那些不允许产生振荡响应的系统外，通常都希望控制系统具有适度的阻尼、较快的响应速度和较短的调节时间。

为了便于说明改善系统动态性能的方法，图片3.5表示了欠阻尼二阶系统各特征参量之间的关系。

图片3.5：欠阻尼二阶系统额定特征参量。

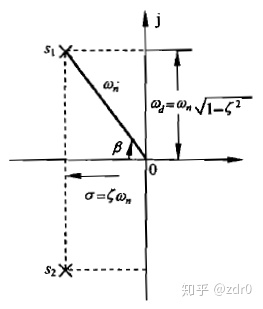
由图片3.5可见，衰减系数

是闭环极点到虚轴之间的距离；阻尼振荡频率

是闭环极点到实轴之间的距离；自然频率

是闭环极点到原点之间的距离；且

与负实轴的夹角恰好是阻尼比，即：

故

称为阻尼角。下面推导无零点欠阻尼系统的动态性能指标计算公式。

延迟时间

：

在式

中，令

，可得

的隐函数表达式为：

利用曲线拟合法，在较大的

范围内，近似有：

在

时，亦可使用式进行近似：

式

和式

表明，增大自然频率或减小阻尼比都可以减小延时时间。或者说，当

不变时，闭环极点距

平面的坐标原点越远，系统的延迟时间越短；而当

不变时，闭环极点距

平面上的虚轴越近，系统的延迟时间越短。

上升时间

：

在式

中，令

，求得：

由于

，所以有：

由式

可知，当阻尼比

一定时，阻尼角

不变，系统的响应速度与

成正比；而当阻尼振荡频率

一定时，阻尼比越小，上升时间越短。

峰值时间

：

对式

对时间求导并令导数为零得：

整理得：

根据峰值时间的定义，有：

式

表明，峰值时间等于阻尼振荡周期的一半。或者说，峰值时间与闭环极点的虚部成反比。当阻尼比一定时，闭环极点离负实轴的距离越远，系统的峰值时间越短。

超调量

：

因为超调量发生在峰值时间上，所以，将式

带入式

可得输出量的最大值为：

由于

，故式

可写为：

根据超调量的定义，并考虑到

可以求得：

式

表明，超调量

是阻尼比

的函数，而与自然频率

无关。显然，阻尼比越大，超调量越小，反之亦然。

调节时间

：

上式表明，调节时间与闭环极点的实部数值成反比。闭环极点距虚轴的距离越远，系统的调节时间越短。由于阻尼比值主要根据系统超调量的要求来满足，所以调节时间主要由自然频率决定。若能保持阻尼比值不变而增大自然频率，则可以在不改变超调量的情况下缩短调节时间。

从上述各项动态性能指标的计算中可以看出，各个指标之间是相互矛盾的。比如上升时间和超调量，即响应速度和阻尼程度不能同时达到满意的结果。

过阻尼二阶系统的动态过程分析

由于过阻尼的系统的响应缓慢，故通常不希望采用过阻尼系统。但是，这并不排除在某些情况下，例如在低增益、大惯性的温度控制系统当中，需要采用过阻尼系统。

当阻尼比

，且初始条件为零时，二阶系统的单位阶跃响应为式

。显然， 在动态性能指标中，只有延迟时间、上升时间和调节时间才具有意义。然而，式

是一个超越方程，无法根据各个动态性能指标的定义求出其精确的计算公式。目前，工程上所采用的方法，仍然是利用数值近似的解法求出不同

值下的无因次时间，然后制成曲线以供查用；或使用曲线拟合法给出近似计算公式。

延迟时间

：

上升时间

：

调节时间

：

由式

，令

为不同的值，可以解出相应的无因次调节时间

。由于：

因此得到：

临界阻尼二阶系统的调节时间为：

---

自动控制原理—胡寿松.