这里是一则小广告:
关注作者请点击这里哦:zdr0
我的专栏里面不仅有学习笔记,也有一些科普文章,相信我的专栏不会让您失望哦~大家可以关注一下:数学及自然科学
-尽力写最好的讲义,尽力写最好的科普。
第一章—自动控制的一般概念
自动控制系统可有多种分类方式。例如,
- 按照控制方式可分为:开环控制、反馈控制、复合控制等;
- 按照元件类型可分为:机械系统、电气系统、机电系统、液压系统、气动系统、生物系统等;
- 按照系统功用分类可分为:温度控制系统、压力控制系统、位置控制系统等;
- 按照系统特性可分为:线性系统和非线性系统、连续系统和离散系统、定常系统和时变系统、确定性系统和不确定性系统等;
- 按照输入量的变化规律可分为:恒值控制系统、随动系统和程序控制系统等。
这类系统可以使用线性常微分方程进行描述。其一般形式为:
其中:
:被控制量;
:系统输入量。
系数
这类系统的输入量是一个常值,被要求控制量亦为一个常值,故该系统又称为调节器。如有扰动,被控制量会偏离输入量而出现偏差,所以,控制系统便会根据偏差产生控制作用,以克服扰动的影响,是被控制量恢复到给定的常值。其中输入量可以按需改变,但一经改变之后仍要保持是常值。
这类控制系统的输入量是预先未知随时间任意变化的函数,要求被控制量以尽可能小的误差跟随输入量的变化,故又称为跟踪系统。在随动系统中,扰动的影响是次要的。系统分析、设计的重点是研究被控制量跟随的快速性和准确性。在随动系统中,如果被控制量是机械位置或其导数时,这类系统成为伺服系统。
这类系统的输入量是按照预先规律随时间变化的函数,要求被控制量迅速准确的加以复现。恒值控制系统可以视为程序控制系统的特例。
一般的,在离散系统中既有连续的模拟信号,也有连续的数字信号,因此,离散系统一般使用差分方程进行描述,其一般形式为:
其中:
:差分方程的次数;
:常系数;
:输入和输出采样序列。
系统中,只要有一个元件的输入和输出特性是非线性的,那么这类系统就称为非线性的控制系统。对于这类系统,又可分为连续的非线性控制系统和离散的非线性控制系统,前者需要使用非线性的微分方程进行描述,而后者则需要使用非线性的差分方程进行描述。在实际的物理系统中,都会含有程度不同的非线性元件,而且由于对于非线性方程的处理比较困难。所以,目前对于非线性系统没有一个统一的研究方法。但是对于非线性程度不太严重的元件,可采用在一定范围内线性化的方法,从而将非线性控制系统近似为线性控制系统。
对每一类系统被控制量变化的全过程提出的共同基本要求都是一样的,且可以归结为稳定性、快速性和准确性。
稳定性是保证控制系统能够正常工作的先决条件。一个稳定的控制系统,其被控制量离期望值的初始偏差应随时间的增长逐渐减小并趋近于零。对于稳定的恒值控制系统,被控制量因扰动而偏离期望值之后,经过一个过渡过程时间,被控制量应该恢复到原来期望值的状态;对于稳定的随动系统,被控制量应该始终跟随输入量的变化。反之,对于,不稳定的控制系统,其被控制量偏离期望值的初始偏差将随时间的增长变得越来越大。
线性自动控制系统的稳定性是由系统结构所决定的,与外界因素无关。这是因为在控制系统中一般含有储能元件或者惯性元件,储能元件的能量不可能发生突变。因此,当系统受到扰动或有输入量的时候,控制过程一般不会立即完成,而是有一定时间的延缓,这就使得被控制量恢复到期望值或跟随输入量有一个时间过程,称为过渡过程。比如在反馈系统中,由于被控制对象的惯性,会使控制动作不能瞬间纠正被控制量的偏差,控制装置的惯性则会使偏差信号不能够及时的完全转化为控制动作。偏差可正可负,这时出现所谓的振荡形式,如果振荡过程是逐渐减弱的,系统最终可以到达平衡状态,控制目的得以实现,我们称之为稳定系统;反之,如果振荡过程不断增强,系统的被控制量将失去控制,则为非稳定系统。
为了更好的完成任务,还必须对系统的过渡过程的形式和快慢提出要求,一般称为动态性能。对系统过渡过程的时间(即快速性)和最大振荡幅度(即超调量)一般都有具体要求。
在实践中,自动控制系统承受外部作用的形式是多种多样的,既有确定性外部作用,又有随机性的外部作用。对于不同形式的外部作用,系统被控制量的相应各不相同。为了方便使用统一的方法研究和比较控制系统的性能,通常选用几种确定性函数作为典型的外作用,可选作典型外部作用的函数应具有以下条件:
- 在实验室中容易得到;
- 控制系统在这种函数的作用下的性能应代表在实际工作条件下的性能;
- 这种函数的数学表达式简单,便于进行理论计算。
特别的,当
例如,雷达-高射炮系统。
脉冲函数还可以表示为:
其中,单位脉冲函数(又称为
第二章—控制系统的数学模型
设由电阻
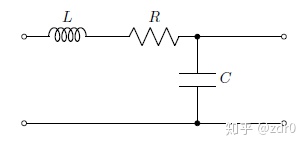
设回路的电流为
且有支路方程:
消去中间变量
显然,式
使用线性微分方程面熟的元件或系统,称为线性元件或线性系统。线性系统的重要性质是可以应用叠加原理。叠加原理具有两层含义,即具有可叠加性和齐次性。线性系统的叠加原理表明,两个外部作用同时加于系统所产生的总输出,等于各个外部作用单独作用时分别产生的输出之和(可叠加性),且外部作用的数值增大若干倍时,其输出亦相应增加相同的倍数(齐次性)。举例说明,二阶线性常微分方程:
若
可参看本人写的常微分方程教程。
zdr0:《数学及自然科学》——目录
除了可以在一定的条件下将非线性元件视为线性元件外,还有一种方法—切线法或最小偏差法。这种线性化的方法特别适用于具有连续变化的非线性特性函数,其实质是在一个很小的范围内,将非线性特性使用一段直线来替代,具体方法如下所述。
设非线性连续函数
当
若将
如果不考虑增量,则得到:
式
对于
其中,
这种小偏差线性化方法对于控制系统的大多数工作状态是可行的。
设铁芯线圈电路如图
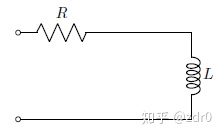
设铁芯线圈磁通量变化时产生的感应电动势为:
由基尔霍夫定律列写回路电压方程有:
方程
当
忽略增量我们可以得到:
将式
在数学上,线性微分方程的解由特解和齐次微分方程的通解组成,通解由微分方程的特征根所决定,它代表的是自由运动。如果
其中,系数
如果特征根中有重根,则模态会具有形如




 本文介绍了自动控制原理的基本概念,包括开环、反馈和复合控制等分类方式,以及线性、非线性,连续和离散系统的描述。通过线性常微分方程和差分方程探讨了控制系统的行为,并强调了稳定性、快速性和准确性作为系统性能的三大关键要素。
本文介绍了自动控制原理的基本概念,包括开环、反馈和复合控制等分类方式,以及线性、非线性,连续和离散系统的描述。通过线性常微分方程和差分方程探讨了控制系统的行为,并强调了稳定性、快速性和准确性作为系统性能的三大关键要素。


















 2798
2798

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








