利用可达矩阵判断连通性_C语言求矩阵的伴随矩阵、逆矩阵、转置矩阵

最新推荐文章于 2024-06-03 14:44:58 发布

最新推荐文章于 2024-06-03 14:44:58 发布 · 560 阅读

文章标签：

#利用可达矩阵判断连通性 #矩阵化为行最简形矩阵计算器 #矩阵最简行阶梯型计算器 #矩阵的逆矩阵怎么求 #行最简形矩阵计算器 #行最简矩阵计算器

本文介绍如何使用C语言实现矩阵的伴随矩阵、逆矩阵及转置矩阵的计算，并提供完整的代码实现。

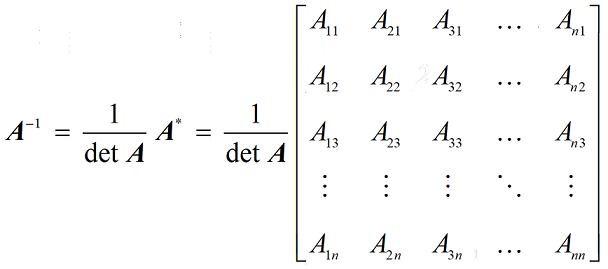
在之前的文章C语言实现行列式计算中，我们已经实现了计算
阶行列式的相关代码，并且已经完成了获取指定元素余子式的函数（本文中改定义为cofactor）. 本文将在行列式计算器的基础上实现计算方阵伴随矩阵和可逆矩阵的计算器的编写.

一、知识储备

• 伴随矩阵：方阵

在阶数高于 1 时的

伴随矩阵

满足

阶数为 1 时，伴随矩阵可以定义为

；

• 逆矩阵：如果方阵

的行列式

，则矩阵

可逆，其

可逆矩阵

和伴随矩阵存在关系：

• 转置矩阵：将矩阵

行列位置互换后得到的矩阵

就是

转置矩阵.

二、基本思路

• 首先输入方阵的阶（order）和方阵本身（matrix）；

• 利用 determinant 函数计算方阵的行列式，判断方阵是否可逆；

• 利用 cofactor 函数计算方阵各个位置元素对应的代数余子式，得出方阵的伴随矩阵；

• 如果方阵可逆，在方阵伴随矩阵的基础上将每个元素均除以方阵的行列式，计算出方阵的逆矩阵.

三、实现方法

• 由于在函数之间传递二维数组不方便，在C语言实现矩阵求秩和化约化阶梯形一文中，我们采用了由函数返回指定行列位置元素的方法（在本问题中确实可以采用直接输出结果，但是考虑到之后矩阵乘法、解矩阵方程的过程会用到伴随矩阵和逆矩阵每个行列位置元素的值，我们在此做提前考虑），在这个问题中，我们采用相同的方法，定义：

float adjugate_matrix(float matrix[20][20],int order,int r,int c);
float inverse_matrix(float matrix[20][20],int order,int r,int c);
float transposed_matrix(float matrix[20][20],int r,int c,int i,int j);

分别用来计算伴随矩阵、逆矩阵、转置矩阵，并返回指定行列位置的元素；

并单独定义三个函数：

void show_inverse_matrix(float matrix[20][20],int order);
void show_adjugate_matrix(float matrix[20][20],int order);
void show_transposed_matrix(float matrix[20][20],int r,int c);

来单独输出伴随矩阵、逆矩阵、转置矩阵.

· 利用高于2阶方阵的伴随矩阵的第

行第

列元素恰好是原矩阵第

行第

列元素对应的代数余子式

这一规律，可以直接得出伴随矩阵；阶数为 1 的伴随矩阵单独处理为 [1] ，则不难写出：

float adjugate_matrix(float matrix[20][20],int order,int r,int c)
{
    float result = 0;

    if(order == 1 && r == 0 && c == 0)
        result = 1;
    else
        result = pow(-1,r + c) * cofactor(matrix,order,c,r);
    if(result <= 0 && result >= -0.0005)
        result = fabs(result);
    
    return result;
}

其中的步骤：

if(result <= 0 && result >= -0.0005)
    result = fabs(result);

是防止之后的输出结果中-0.000的出现；

利用逆矩阵的每个元素即为伴随矩阵每个元素除以行列式的值（行列式不为 0），可得

float inverse_matrix(float matrix[20][20],int order,int r,int c)
{
    float result = 0;
    
    result = adjugate_matrix(matrix,order,r,c) / determinant(matrix,order);
    if(result <= 0 && result >= -0.0005)
        result = fabs(result);
    
    return result;
}

转置矩阵就非常简单了，只需：

float transposed_matrix(float matrix[20][20],int r,int c,int i,int j)
{
    return matrix[j][i];
}

即可.

同时，我们还需要下面三个函数输出计算结果：

void show_inverse_matrix(float matrix[20][20],int order)
{
    int i,j;
    
    for(i = 0;i < order;i ++)
    {
        for(j = 0;j < order;j ++)
            printf("%.3ft",inverse_matrix(matrix,order,i,j));
        printf("n");
    }
}

void show_adjugate_matrix(float matrix[20][20],int order)
{
    int i,j;
    
    for(i = 0;i < order;i ++)
    {
        for(j = 0;j < order;j ++)
            printf("%.3ft",adjugate_matrix(matrix,order,i,j));
        printf("n");
    }
}

void show_transposed_matrix(float matrix[20][20],int r,int c)
{
    int i,j;
    
    for(i = 0;i < c;i ++)
    {
        for(j = 0;j < r;j ++)
            printf("%.3ft",transposed_matrix(matrix,r,c,i,j));
        printf("n");
    }
}

本程序的计算功能就基本完成了.

但是，我们还要注意几点：

如果矩阵不是方阵，就无所谓伴随矩阵和逆矩阵；
当方阵的行列式为 0，方阵不存在逆矩阵.

我们把上述判断写入主函数中，并加入适当的提示与引导，得到全过程的代码:

#include <stdio.h>
#include <math.h>

float determinant(float matrix[20][20],int order);
float cofactor(float matrix[20][20],int order,int r,int c);
float adjugate_matrix(float matrix[20][20],int order,int r,int c);
float inverse_matrix(float matrix[20][20],int order,int r,int c);
float transposed_matrix(float matrix[20][20],int r,int c,int i,int j);
void show_inverse_matrix(float matrix[20][20],int order);
void show_adjugate_matrix(float matrix[20][20],int order);
void show_transposed_matrix(float matrix[20][20],int r,int c);
void menu(void);

int main()
{
    float matrix[20][20];
    int r,c,i,j,choice;
    
begin:
    printf("输入矩阵的行规模:");
    scanf("%d",&r);
    printf("输入矩阵的列规模:");
    scanf("%d",&c);
    printf("输入一个 %d × %d 矩阵:n",r,c);
    for(i = 0;i < r;i ++)
        for(j = 0;j < c;j ++)
            scanf("%f",&matrix[i][j]);
menu:
    menu();
    scanf("%d",&choice);
    if(choice == 1)
    {
        if(r != c)
            printf("非方阵不存在伴随矩阵!n");
        else
        {
            printf("矩阵的伴随矩阵为:n");
            show_adjugate_matrix(matrix,r);
        }
        goto menu;
    }
    else if(choice == 2)
    {
        if(r != c)
            printf("非方阵不存在逆矩阵!n");
        else
            if(determinant(matrix,r) == 0)
                printf("方阵不存在逆矩阵!n");
            else
            {
                printf("矩阵的逆矩阵为:n");
                show_inverse_matrix(matrix,r);
            }
        goto menu;
    }
    else if(choice == 3)
    {
        printf("矩阵的转置矩阵为:n");
        show_transposed_matrix(matrix,r,c);
        goto menu;
    }
    else if(choice == 0)
        goto end;
    else
    {
        printf("指令错误，重新输入!n");
        goto menu;
    }

end:
    return 0;
}

float determinant(float matrix[20][20],int order)
{
    float result = 0,sign = 1;
    int i;
    
    if(order == 1)
        result = matrix[0][0];
    else
        for(i = 0;i < order;i ++)
        {
            result += sign * matrix[i][0] * cofactor(matrix,order,i,0);
            sign *= -1;
        }
    
    return result;
}

float cofactor(float matrix[20][20],int order,int r,int c)
{
    float result = 0,cofactor[20][20];
    int original_i,original_j,i,j;
    
    for(i = 0;i < order;i ++)
        for(j = 0;j < order;j ++)
        {
            original_i = i;
            original_j = j;
            if(i == r || j == c);
            else
            {
                if(i > r)
                    i --;
                if(j > c)
                    j --;
                cofactor[i][j] = matrix[original_i][original_j];
                i = original_i;
                j = original_j;
            }
        }
    if(order >= 2)
        result = determinant(cofactor,order - 1);
    
    return result;
}

float adjugate_matrix(float matrix[20][20],int order,int r,int c)
{
    float result = 0;

    if(order == 1 && r == 0 && c == 0)
        result = 1;
    else
        result = pow(-1,r + c) * cofactor(matrix,order,c,r);
    if(result <= 0 && result >= -0.0005)
        result = fabs(result);
    
    return result;
}

float inverse_matrix(float matrix[20][20],int order,int r,int c)
{
    float result = 0;
    
    result = adjugate_matrix(matrix,order,r,c) / determinant(matrix,order);
    if(result <= 0 && result >= -0.0005)
        result = fabs(result);
    
    return result;
}

float transposed_matrix(float matrix[20][20],int r,int c,int i,int j)
{
    return matrix[j][i];
}

void show_inverse_matrix(float matrix[20][20],int order)
{
    int i,j;
    
    for(i = 0;i < order;i ++)
    {
        for(j = 0;j < order;j ++)
            printf("%.3ft",inverse_matrix(matrix,order,i,j));
        printf("n");
    }
}

void show_adjugate_matrix(float matrix[20][20],int order)
{
    int i,j;
    
    for(i = 0;i < order;i ++)
    {
        for(j = 0;j < order;j ++)
            printf("%.3ft",adjugate_matrix(matrix,order,i,j));
        printf("n");
    }
}

void show_transposed_matrix(float matrix[20][20],int r,int c)
{
    int i,j;
    
    for(i = 0;i < c;i ++)
    {
        for(j = 0;j < r;j ++)
            printf("%.3ft",transposed_matrix(matrix,r,c,i,j));
        printf("n");
    }
}

void menu(void)
{
    printf("n");
    printf("[1]求伴随矩阵.n");
    printf("[2]求逆矩阵.n");
    printf("[3]求转置矩阵.n");
    printf("[0]结束.n");
    printf("输入你的选择:");
}

本程序大功告！

综合目前的三篇文章，我们可以将关于矩阵和行列式的全部功能编入一个头文件"matrix.h"中，以方便之后在向量范畴和其他线性代数范畴中更加便捷的调用相关的函数功能.

本文的方法并非最简，仅分享本人的一点想法，如有不当之处，还请各位在评论区指正！