
0 序言
泰勒公式,本质上是一种函数的近似,强大之处就在于可以将不同类型的函数,统一用多项式求和的形式进行替换,从而变成多项式的运算。
本篇主要是标出常见的几个泰勒展开式、高阶无穷小的计算规则、泰勒公式使用时应该展开到第几项以及泰勒公式的应用。
1 常见的泰勒公式

【记忆】
一般情况下,考研只会考到某一基本函数展开式x的3到4次方,因为题目大多数都是有两个及以上基本函数相乘或者复合函数等来进行出题,这样的计算量可能就到5甚至6次方了,所以我们记忆时一般最多只需要记到4次方项就可以了。
我们可以看到,(1)~(4),都是奇函数,所以记住x只会有奇数次方,(1)和(2)、(3)和(4)的第2项系数相反,这样我们记住(1)(3)就容易可以想起(2)(4),(5)的cos是sin的导数,所以记住(1)亦可推出(5)。
【注】以上8个泰勒公式应该是考研里面最常考的了,其中,这里的x可以广义化,当
因此,可以引申出下面也相对常见的几种泰勒公式:

由上面的泰勒公式,可以得到常见的等价无穷小代换:
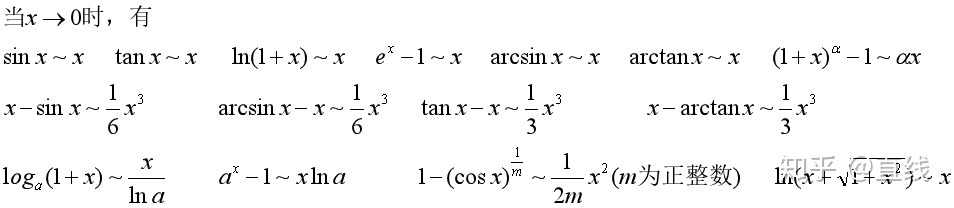
其中,

当然,等价无穷小代换时,x也可以进行广义化,题目一般都是广义化的无穷小量,大家可以以记泰勒公式为主,然后由泰勒公式直接得到等价无穷小代换,对一些不熟悉的或者不能直接从泰勒公式看出来的,再加强记忆。
2 高阶无穷小的计算规则
下面
(1) 高阶无穷小加减
(2) 高阶无穷小与幂函数之乘积
(3) 高的高阶无穷小与低的高阶无穷小之商
(4) 有界函数与高阶无穷小乘积
【注】理解和掌握这些计算规则,有助于我们理解在下面的进行泰勒公式展开时,应该展开到第几项的分析。

3 展开到第几项
对于泰勒公式的应用,除了公式相对比较难记外,展开式需要到第几项有时也是我们所疑惑的,展开项不足时容易漏项甚至有时候出现相减为0,展开项多了就难免增加计算量。在这里,主要介绍两个原则,分别是分式“上下同阶”原则、加减“幂次最低”原则。
分式“上下同阶”,简单来说,如果分母(或分子)是x的k次方,则应该把分子(或分母)展开到x的k次方。(一般情况都是看分母然后决定分子的展开)

加减“幂次最低”,如A-B,简单来说,就是将A、B分别展开到它们的系数不相等的x的最低次幂为止。

下面举个基础的题目例子,用泰勒公式来对上面的两个原则做进一步的解释分析:

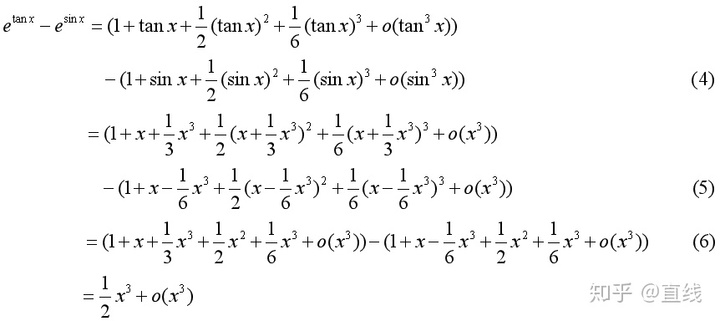

【注】当然,仅仅对于这道题而言,用泰勒公式并不是最方便的,我只是觉得这道题方便我对两个原则进行说明,以及在泰勒公式展开时应该注意的点和简化时的技巧。
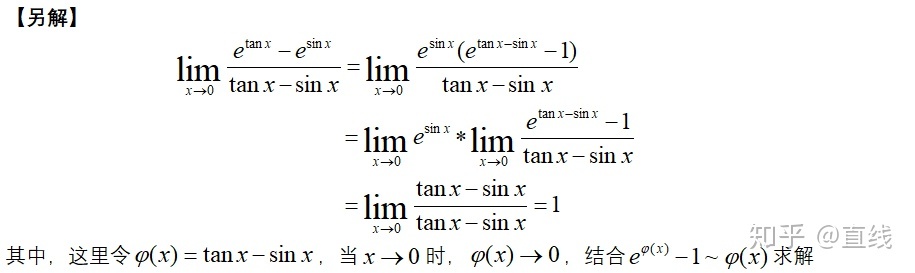







 本文深入探讨泰勒公式,包括常见泰勒展开式、高阶无穷小计算规则和展开项的选择。泰勒公式用于函数近似,常见于考研数学。文中列举了8个考研常考泰勒公式,并强调了高阶无穷小的加减、乘幂及商的计算规则,以及展开项选择的两个原则:分式“上下同阶”和加减“幂次最低”。
本文深入探讨泰勒公式,包括常见泰勒展开式、高阶无穷小计算规则和展开项的选择。泰勒公式用于函数近似,常见于考研数学。文中列举了8个考研常考泰勒公式,并强调了高阶无穷小的加减、乘幂及商的计算规则,以及展开项选择的两个原则:分式“上下同阶”和加减“幂次最低”。
















 7052
7052

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








