matlab 1到无穷_MATLAB数值微分与数值积分

点击上方蓝字  关注我们

从本节开始，我们将进入matlab的数值微积分与方程求解模块，一起学习如何利用matlab去解决微积分问题。

对于本节内容，主要分为两个部分讲解，数值微分和数值积分，那么下面，就开始今天的学习吧！

一、数值微分

在正式开始之前，有几个新概念需要讲解一下(1) 数值差分与差商：微积分中 ，任意函数 f(x) 在x0 点的导数是通过极限定义的(如下图所示)：

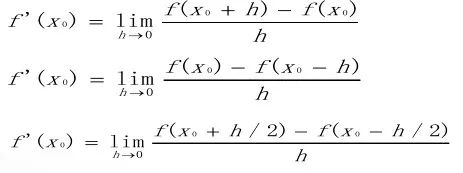
如果去掉极限定义中h趋向于0的极限过程，得到函数在x0 点处以h( h>0 )为步长的向前差分、向后差分和中心差分公式(如下图)：

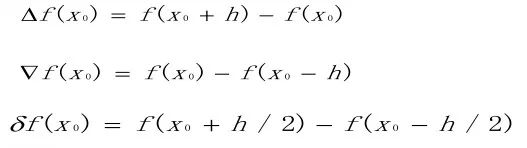
当步长h充分小时，得到函数在x0 点处以h( h>0 )为步长的向前差商、向后差商和中心差商公式(如下图)：

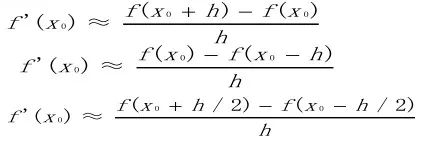
函数 f(x) 在 点x0的微分接近于函数在该点的差分，而f在点x的导数接