定积分计算器_浅谈科学计算器的定积分功能

【作者声明】

　　本文所有文字均为作者原创，所有图片均为作者本人亲自拍摄或制作。

　　版权所有，仅供阅读欣赏，禁止任何单位或个人以任何形式对本文的文字或图片进行包括但不限于复制、转载、引用、抄袭、截图、模仿、翻译、印刷等之中的一项或多项的行为。禁止将本文用于商业用途。

　　作者保留所有权利，请尊重作者的劳动成果，谢谢合作。

前言

　　定积分功能是相对高端的科学计算器上具备的功能之一，因为在许多实际使用场合下免去了人工计算积分的繁琐，所以应用也十分广泛。科学计算器上的定积分一般都是采用数值积分的方法来完成定积分的计算，虽然数值积分有许多理论上的方法，但从上世纪80年代到现在，计算器上使用的数值积分的方法只出现过两种。早期是辛普森积分法，到本世纪初有部分计算器开始使用高斯积分法。那么这两类数值积分方法的具体原理是什么？使用的效果有何特点？各自的优缺点是什么？至今为止没有任何计算器的说明书或者计算器的相关资料给出过答案。这些问题就是我们这篇文章要讨论的。

两种定积分功能简述

辛普森积分法

辛普森（Simpson）数值积分法在上世纪80年代的计算器上就已经出现了。例如上世纪80年代初的卡西欧可编程计算器fx-180P，通过按键编程的方式记录被积函数，然后进入积分的模式（∫dx），指定分区数

，然后输入积分的下限和上限，等待一段时间就能计算出积分结果，详细介绍可参考文章：《CASIO早期可编程函数计算器简介》。下图是计算

，取分区数为7，得到的近似积分值0.69314718。

　　从W系列（fx-991W）开始，卡西欧旗舰科学计算器型号上开始加入定积分功能，例如fx-991MS就是使用的辛普森积分法：

　　TI的单行显示科学计算器与双行显示科学计算器（例如TI-36X II）也采用辛普森积分法来计算定积分，不过分区数的输入范围只能是1到99之间任意的整数。例如TI的可编程科学计算器TI-55 II，分区数指定为64时，积分的结果是0.6931472。（图片由 @小林露露 友情提供）

　　又比如夏普的EL-W991TL，也是使用的辛普森积分法：

　　使用辛普森积分法的计算器，分区数的输入都可以省略，计算器会自动指定一个合适的分区数。

高斯积分法

　　计算器上使用的高斯积分法是高斯-克朗罗德（Gauss-Kronrod）数值积分法。这一方法在2004年的卡西欧ES系列开始使用，经过对比会发现ES系列计算器使用该方法计算定积分的时候，不仅比MS系列快，而且精度还很高。在自然数学输入方式下，用户只需要输入被积式即可，而在线性输入方式下，用户还可以指定一个所谓的“公差值”。这里以fx-991CN X为例，同样是计算

：

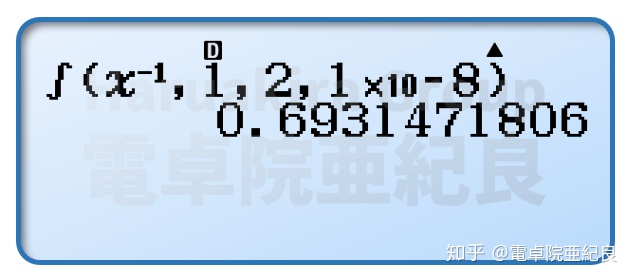
　　不仅是卡西欧，TI的MathPrint科学计算器、图形计算器也基本上都是采用的高斯积分法。

　　不论是哪一款科学计算器，使用定积分功能的时候需要注意被积函数里面有三角函数或者反三角函数的时候，必须以弧度制为角度单位，这也是很多人在用计算器计算定积分的时候容易出现问题的地方。

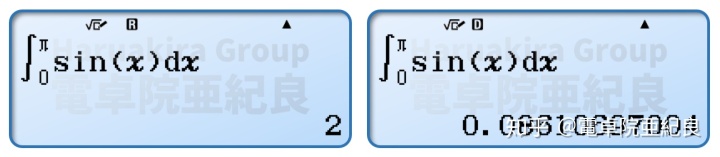
两种定积分功能的计算原理与计算器的内部算法

辛普森积分法

　　最简单的数值积分法是矩形法，而为了提高计算的精度，辛普森积分法用抛物线段代替每一小区间内的被积函数曲线段。

　　辛普森积分法的公式：用分点

把区间

分成

（偶数）个长度相等的小区间，各分点对应的函数值为

，则有

　　当

越大的时候，和积分真值的近似程度就越高。

　　对于计算器来说，如果只是应用上面的公式计算，那么最终结果的准确性是不可得知的，因为计算器的内部计算过程都是按照计算器本身的内部计算有效数字位数进行的。

　　我们举一个例子：计算

。夏普给的结果是：

　　可以看到，从第7位有效数字开始就不准确了，然而到第几位是准确的，从计算器上我们也无从得知。不过卡西欧的计算器倒是对结果作了处理，例如fx-991MS在分区数为9的时候，给出的结果是2.64878，耗时大约59.5秒：

　　进一步观察，在不同的分区数下，卡西欧的计算器似乎是对辛普森法的准确程度进行了评估，然后取相应的有效数字位数之后，再给出结果。以

为例，fx-991MS在不同分区数下算出的结果如下：

n＝1：2.
n＝2：2.02
n＝3：2.02
n＝4：2.0201
n＝5：2.02006
n＝6：2.020059
n＝7：2.0200586
n＝8：2.020058624(4782)
n＝9：2.020058624(4364)
【注：括号内是新版fx-991MS未显示出的位数，或许是因为已经满足显示10位的要求，不再舍去后续的内部计算的有效数字位数。】

　　从上面的结果可以看到，卡西欧的计算器在辛普森积分法的基础上，确实是对辛普森法的计算结果的准确度作了评估，每个分区数下显示的结果基本上都能精确到最后一位。此外，逐渐增大分区数，计算所用的时间也越来越长。

【注：辛普森积分法是可以计算截断误差的，根据截断误差可以判断到第多少位有效数字都是精确的，详细的内容可以查阅相关资料。】

高斯积分法

　　对于定积分

，其中

是区间

上的权函数，在区间

上取

个互异的节点

，则有数值积分公式

，

　　其中，

是与

无关的积分系数，由下式算出：

　　这里的

是

次正交多项式，

是其零点。

　　高斯积分法的原理比辛普森积分法复杂很多，一般都是给定求积节点和求积系数，直接近似计算在某个区间下（最常见的就是

，其他区间需要作区间变换）的定积分了。

　　经过实际的测试，计算器上的高斯积分法的速度和精度远远优于辛普森积分法。同样是计算

，fx-991CN X给出的结果是：

　　可以看到，不仅精度高，而且速度非常快，只用了3.5秒。（注：fx-991CN X因为硬件速度较以前的型号提升了几倍，所以非常快。经过测试，这个积分在fx-991ES PLUS上的耗时是16.5秒，相比于fx-991MS，不仅精度提高到至少10位，而且出结果的速度是三倍以上。）

　　高斯-克朗罗德数值积分法使用

个节点，以15节点的高斯-克朗罗德数值积分法为例，在区间

上积分节点和系数分别为：

±0.9914553711，0.02293532201
±0.9491079123，0.06309209263
±0.8648644234，0.1047900103
±0.7415311856，0.1406532597
±0.5860872355，0.1690047266
±0.4058451514，0.1903505781
±0.2077849550，0.2044329401
0，0.2094821411

　　我们在fx-4500PA上编程进行测试，以

为例，使用自带的定积分功能（使用计算器自动指定的分区数）算出的结果是12.07，而使用15节点的高斯-克朗罗德数值积分法编程算出的结果是12.07034632。

　　在线性输入方式下，卡西欧的计算器提供了“公差值”的输入，这个值越小计算的精度越高，最小不小于

，而数学自然输入方式下统一使用

作为“公差值”。可以

推测计算器是根据不同的“公差值”来产生不同的积分节点和系数。

两种方法的优缺点

　　经过上面的分析，可以看出辛普森积分法如果分区数很少，计算的速度会特别快，但相应的精度就会很低。在不要求定积分的精确值的时候，使用辛普森法的计算器可能给出结果的速度会相当快，尤其是卡西欧的计算器，在对辛普森法的准确度进行评估的基础上，计算结果的所有有效数字基本上可以认为都是准确的。也就是说，辛普森法的优缺点非常明显：
　（1）精度要求低的时候计算速度快，精度要求高的时候计算速度慢；
　（2）如果函数在积分区间内波动幅度较大，或者斜率变化大，辛普森积分法的效果就会变差；
　（3）当区间范围非常大的时候，由于分区数有限，也可能产生较大的误差。
　　不过，在大多数场合，辛普森法无法给出相对精确的结果，因此目前大多数科学计算器都抛弃了这一算法，只有卡西欧的MS系列、TI的双行计算器、夏普的科学计算器仍然在继续使用。

　　高斯积分法不再受分区数的限制，积分的时间也大大缩短，而且精度也大幅提高，所以目前大多数有定积分功能的计算器都是采用的这一算法，这也是为什么大家现在都倾向于使用fx-991CN X，硬件水平的提升带来的是定积分、连加求和等复杂计算用时大大缩短的好处，这些都说明高斯积分法的优点确实很多。即使优点再多，也必然存在缺点。当积分区间范围太大的时候，高斯积分法的弊病就出来了。我们看fx-991CN X计算概率积分的例子：

　　积分区间是

时，积分的结果是1（其实积分区间是

时就已经是1了），但积分区间写成

的时候，计算器很快就给出了“0”的结果，这就是计算器使用的高斯积分法的弊病所在，因为按照前面的分析，区间变换是线性的，区间长度越大，而积分节点有限的情况下，如果被积函数的值几乎0，那么很大可能对于每个节点的

都为0。假设这个积分用了51个节点，计算第27个节点（

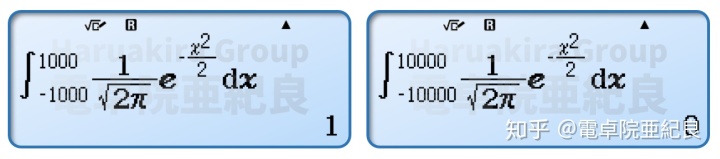
）的函数值是：

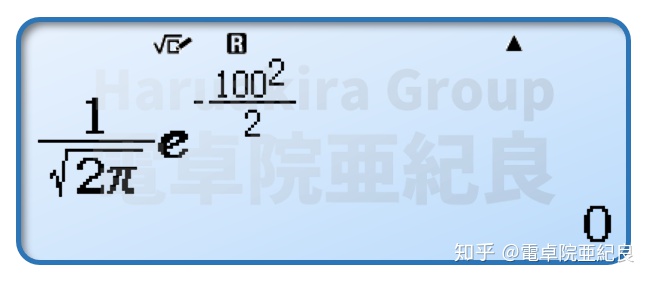
　　所以对于区间范围非常大的积分，对于

的函数，高斯积分法

极有可能出现结果异常的情况。这也就是为什么我们在電卓院亜紀良：使用计算器实现反常积分的计算​zhuanlan.zhihu.com

这篇文章里面讲如何使用计算器计算反常积分（广义积分）的时候，要作积分换元

的缘故，因为这样可以将类似

这样的区间变换成

，然后高斯积分法就可以再发挥作用了。这个方法非常实用，我们甚至可以在fx-991CN X上实现伽马（Gamma）函数的计算：

如何用科学计算器算伽马函数？​www.zhihu.com

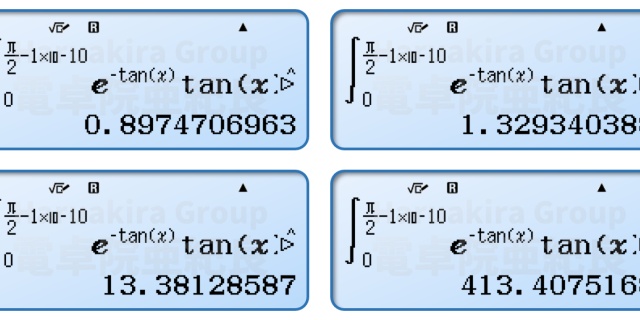
所以，针对上面结果异常的情况，用换元积分法就能解决了：

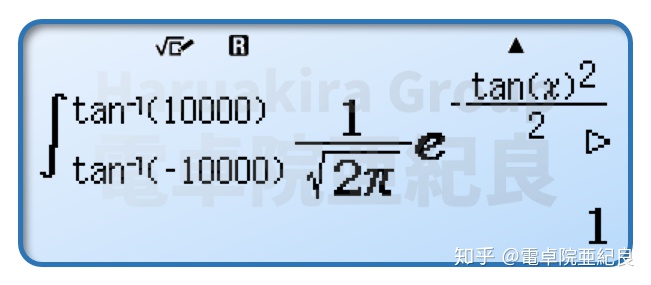
　　综合以上分析来看，计算器使用高斯积分法作为内置定积分算法的好处是远远大于辛普森积分法的。

总结

　　这篇文章简单地介绍了科学计算器上定积分功能，然后从算法的数学原理的角度分析了计算器上的辛普森积分法与高斯积分法的特性。因此我们在使用计算器上的定积分功能时，除了需要注意角度单位的设置之外，还应当了解计算器计算定积分的算法原理，以便掌控定积分数值计算结果的精度以及准确度。这篇文章也为研究计算器功能提供了一个很好的例子，分析计算器某一功能的特性，从计算方法与数学原理出发，能够挖掘出这个功能更深层次的内涵。