matlab计算消失点,一种基于消失点运算的相机标定法的制作方法

本发明属于3d视觉测量领域，一种基于消失点运算的双目相机内参及外参的标定方法。

背景技术：

在3d视觉测量中，为得到物体的三维数据，首先需要对双相机进行参数标定，得到相机的像心、像距，双相机的相互位置等参数，然后利用这些参数才能计算待测物的真实三维坐标。因此，在3d视觉测量中，双相机标定方法的可行性、准确性、稳定性显得十分关键！目前的相机标定方法中，传统相机标定法，使用三维或平面型标定物，使用复杂的数学模型及算法，难于广泛应用。主动视觉自标定法，标定物简单，但需要相机作直线运动、正交、旋转等特定的精确运动，实验条件要求高，标定设施昂贵。

本方法结合传统标定法与主动标定法，使用现有技术易于制作的标定物，结合消失点的特性进行运算，得到算法简单，精度稳定可靠的相机标定法。能大幅降低应用上的对接难度，有利于3d视觉技术的推广。可广泛应用于3d测距、3d人脸、地形扫描、车辆定位、建筑物体积计算等。

技术实现要素：

基于此，本发明的目的在于提供一种更为易于应用，算法简单可靠的双目相机标定方法。为达到上述目的，本发明提供技术方案如下：

s1：标定物上带有相互垂直的两组平行线特征，双目相机从不同位置对标定物进行拍图；

s2：利用相互垂直的两组平行线，其消失点到光心连线也垂直的特点进行运算，标定相机内部参数；

s3：利用消失点到光心连线与光轴的夹角，以及标定物的大小，计算双相机的角度及位置，标定相机外部参数。

步骤s1

标定物具有两组已知的平行线特征，且这两组平行线特征相互垂直，如方格板、矩形阵列的圆点阵列板、方形地板砖、建筑墙面或立方形体等。双目相机安装好后，在保证清晰、明亮的条件下，从多个角度对标定物拍照，拍摄3张以上。

步骤s2

本步骤标定内参：像心坐标c(xc，yc)，像距f，像元尺寸s。

根据平行线消失点的重要性质：消失点到光心的连线，与形成该消失点的平行线平行。

所以，对于相互垂直的两组平行线，其形成的两个消失点到光心的连线也垂直。根据这一特性，在此引入向量的数量积运算，即两垂直向量的数量积为0，以此求解相机内参。

1、如图3所示，设像平面为基准平面，最左下角像元点为零点。求解相机内参，需要将像元坐标与实际空间坐标进行变换。若测得两消失点a，b在像平面上所处的像元坐标为(u1,v1)、(u2,v2)。引入像元物理尺寸s，则两消失点的实际空间坐标为a(u1s,v1s,0)、b(u2s,v2s,0)。

像心坐标为c(xc，yc，0)，像距为f，光心o的空间坐标为(xc，yc，f)，则oa，ob的向量a,b表示如下：

a=(u1s-xc，v1s-yc，-f)，b=(u2s-xc，v2s-yc，-f)

因oa垂直ob，所以a·b=0，即：

(u1s-xc)(u2s-xc)+(v1s-yc)(v2s-yc)+f2=0。

利用其它角度拍摄的另外两幅图片，如上同样方法列式，得到三组方程，求解方程组，能够求得xc，yc，f的解均为关于s的倍数(假设分别为k1，k2，k3倍)，即求得：

xc=k1s，yc=k2s，f=k3s

k1，k2实际即为像心c所处的像元坐标，即像心c的像元坐标为(k1，k2)。

2、如图4所示，在后续的应用中，利用相机内参进行空间点的测量，假设有空间某点p，其成像点p’在像平面位置为(ups,vps)，根据针孔成像模型，p点一定处在直线op’上。

在op’与光轴oc形成的平面内，直线op’可表示为：y=(cp’/oc)x

cp’=((ups-k1s)2+(vps-k2s)2)1/2，oc=f=k3s

通过cp’/oc能够发现，像元尺寸s在这里被约去了，即在此直线上，p点的真实位置与s的取值无关。所以对于这种求解方法，在后续的实际应用上，s可取任意值(s≠0)，也可取相机厂家给定的值，不会影响实际空间点的求取计算。这里为了计算方便，我们取s=1，即求得内参：

xc=k1，yc=k2，f=k3，s=1

更进一步地，可多选几组照片进行计算，得到多组xc，yc，f值，剔除较大偏离样本，再求平均值，得到更为准确的相机内参。

步骤s3

本步骤标定外参：双相机的角度偏移θ，位置偏移(m,n)。

利用同一平行线在两相机分别形成的消失点，计算两消失点到光心连线与光轴的夹角，标定双相机的夹角；再利用标定物的已知大小及成像点位置，求解双相机的位置，标定外部参数。

通过步骤s2获得了像心c的像元点坐标(k1，k2)，后续的成像点均以c点为原点来标示像元点坐标。在双相机系统中，我们以左相机为基准，设左相机光心o1为空间零点，左相机光轴为x轴。假定左右相机只在平面内位置错开，右相机相相对于左相机位移为(m，n)，与左相机光轴夹角为θ。

1、如图5所示，设某平行线特征在两相机分别形成了消失点a(u1,v1)、b(u2,v2)，在xy平面内，消失点到光心的连线，与左右相机光轴的夹角分别为α、β。

则有：α=arctan(u1/f1)，β=arctan(u2/f2)

因两消失点到光心的连线均与该平行线特征平行，所以两消失点到光心的连线也相互平行，因此，两相机光轴的夹角θ=α-β。

2、引入标定物大小，标定双相机位置偏移。

如图6所示，设标定物上的点p(xp,yp,zp)，在两相机的成像点为p1(u1,v1)及p2(u2,v2)，设o1、o2、p1、p2的空间坐标分别为：o1(x1,y1,z1)，o2(x2,y2,z2)，p1(x3,y3,z3)，p2(x4,y4,z4)。

p点处于直线o1p1与o2p2的交点上，由此可列出两条直线的方程，三角法求解p点坐标：

(xp-x1)/(x3-x1)=(yp-y1)/(y3-y1)=(zp-z1)/(z3-z1)

(xp-x2)/(x4-x2)=(yp-y2)/(y4-y2)=(zp-z2)/(z4-z2)

代入f1、f2、u1、v1、u2、v2、θ等已知值，并根据角度算出右相机的相关坐标变换，能够求得xp,yp,zp相对于m、n的关系，均为am+bn的关系，假设分别求得为：

xp=a1m+b1n，yp=a2m+b2n，zp=a3m+b3n

同理，对于标定物上另一点q(xq,yq,zq)，同样也可求得xq,yq,zq相对于m、n的关系式。

已知pq=d，则可列出两点距离式：

(xq-xp)2+(yq-yp)2+(zq-zp)2=d2

利用标定物上的另外两点再列式，两个这样的方程，即可求得m和n。最多会有四组m、n的值，根据实际情况舍去三组(如舍去n<0的两组负值，交叉计算距离，再舍去第三组)。

求出θ、m、n几个外参后，后续实际测量应用中，只要测得空间某点a在两相机上的成像点位置(u1,v1)，(u2,v2)，就可以利用本节所述的三角法，求解该点的坐标(xa,ya,za)了。

附图说明

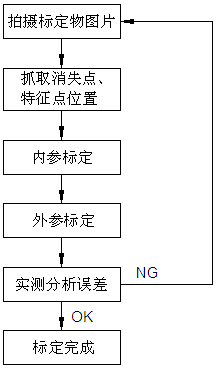
图1是本发明的方法流程图；

图2是本发明实施例实物图；

图3是消失点与光心连线垂直示意图；

图4是针孔成像模型示意图；

图5是消失点与双相机夹角关系示意图；

图6是三角法求解示意图；

图7是误差验证拍样图。

实施例

下面结合附图，对本发明作进一步说明。

如图1所示，本发明的方法流程图，具体实施例步骤如下：

1、如图2所示，本发明实施例的设备实物图。准备好相机(本实施例采用1/3寸640*480像素相机)，标定板；合适的距离安装在三角架安装板上；调整好双相机的角度、焦距、光圈，使标定板清晰明亮可见；然后将双相机的位置、焦圈、光圈等都加以固定住，准备进行相机标定。

2、调整标定板位置，使其在不同的3个方向做倾斜放置，双相机从多个角度对标定板进行拍照。以图片左下角点为0点，根据图片求得各图片的消失点像元坐标。

根据步骤s2的方法，取像元尺寸s=1，求得双相机的各内参如下：

左相机像心坐标：xc1=333，yc1=231，像距f1=2384，像元尺寸s=1

右相机像心坐标：xc2=323，yc2=229，像距f2=2386，像元尺寸s=1。

3、标定板向后倾斜，双相机拍图。以像心c作为基准，求得左右相机消失点的像元坐标。再根据步骤s3的方法，求得双相机光轴的夹角为：θ=20.870。

根据步骤s3的方法，利用标定板四个角点的坐标，及两对角线的长度为212.1mm，列出两距离方程如下：

0.042m2+0.489n2-0.175mn=212.12

0.429m2+0.484n2-0.142mn=212.12

解方程组，舍去n<0的值，求得m，n的值如下：

m=-48.3，n=294.5。

4，实测误差验证

如图7所示，对边长为150mm的标定板拍图，并以像心为基准抓取abcd四个角点的像元坐标，利用内参外参，根据步骤s3的方法，算得每个角点的空间坐标如下：

a点：x=713，y=67，z=75

b点：x=788，y=-64，z=71

c点：x=787，y=-60，z=-81

d点：x=715，y=71，z=-77。

根据距离公式,求得各边长及对角线长度，以及测量误差如下：

边长ab=150.8mm，实际值150mm，测量误差0.5%

边长bc=151.5mm，实际值150mm，测量误差1.0%

边长cd=150.0mm，实际值150mm，测量误差0.0%

边长da=152.1mm，实际值150mm，测量误差1.4%

对角线ac=213.9mm，实际值212.1mm，测量误差0.8%

对角线bd=213.5mm，实际值212.1mm，测量误差0.1%。

上述结果表明，200mm左右的测量范围内，本系统的平均测量误差控制在1%左右，达到了较高的准确性。本系统采用低分辨率1/3寸普通相机，普通标定板，若采用更加专业的硬件，多次校准修正，能得到更高的测量精度。

本发明提供的校正方法算法简单直接，精度可靠，能大幅降低应用上的对接难度，有利于3d视觉测量技术的广泛推广。

最后说明的是，上述实施例，仅为本发明的具体实施方式，用以说明本发明的技术方案，而非对其限制，本发明的保护范围并不局限于此。尽管参照前述实施例对本发明进行了详细的说明，本领域的技术人员应当理解，任何熟悉本技术领域的技术人员在本发明揭露的技术范围内，其依然可以对前述实施例所记载的技术方案进行修改或可轻易想到变化，或者对其中部分技术特征进行等同替换；而这些修改、变化或者替换，并不使相应技术方案的本质脱离本发明实施例技术方案的精神和范围，都应涵盖在本发明的保护范围之内。本发明的保护范围应以所述权利要求的保护范围为准。