三角波的傅里叶变换对_傅里叶变换（二）—傅里叶变换的推导

        “傅里叶”这个名字，我相信对很多人来说并不陌生。尤其是理工科的童鞋，对这三个字应该是如雷贯耳。

      一直以来，在我们的大学专业课本中，“傅里叶”都保持着极高的出镜率。围绕这三个字的一系列名词，例如傅里叶变换、傅里叶积分、傅里叶级数，傅里叶分析等等，曾经让无数人苦不堪言、生不如死，甚至形成了长期的心理阴影。

傅立叶变换，表示能将满足一定条件的某个函数表示成三角函数(正弦和/或余弦函数)或者它们的积分的线性组合。在不同的研究领域，傅立叶变换具有多种不同的变体形式，如连续傅立叶变换和离散傅立叶变换。最初傅立叶分析是作为热过程的解析分析的工具被提出的。

(一)、过程解析

我们先把傅里叶级数转换为指数形式：

三角函数形式：

代入欧拉公式：

可以变形为：

将  、  代入傅里叶级数求得：

将(2)、(3)、(4)代入得：

同理可得： 

将两式代入到(5)中解得：

(注：当  时： )

公式(6)为傅里叶级数的指数形式

然后我们来仔细研究下公式(6)

聪明的你，一定可以看出来这个累加式子非常像积分的黎曼和。

积分表达式的黎曼和表达式：

其中  为步长.同理我们有：

设  ，得到：

我们令  即可得到一个标准化的傅里叶变化公式：

其中

(二)、性质

对称性质

若，则。

奇偶性质

若 ，且 ，其中

表示 的实部， 表示的虚部，则是关于 的奇数，的模是关于的偶函数，辐角是关于的奇函数。

线性性质

若，，则

，其中α和β为常数。

时移性质

若，则

频移性质

若，则。

尺度变换性质

若，则

卷积定理

时域卷积定理：若，，则

频域卷积定理：若，，则

。

时域微、积分

微分性质：

若，则，

积分性质：

若，则

频域微、积分

微分性质：

若，则

积分性质：

若，则

(三)、常用傅里叶变换及其对偶关系图

(下面附下载地址)

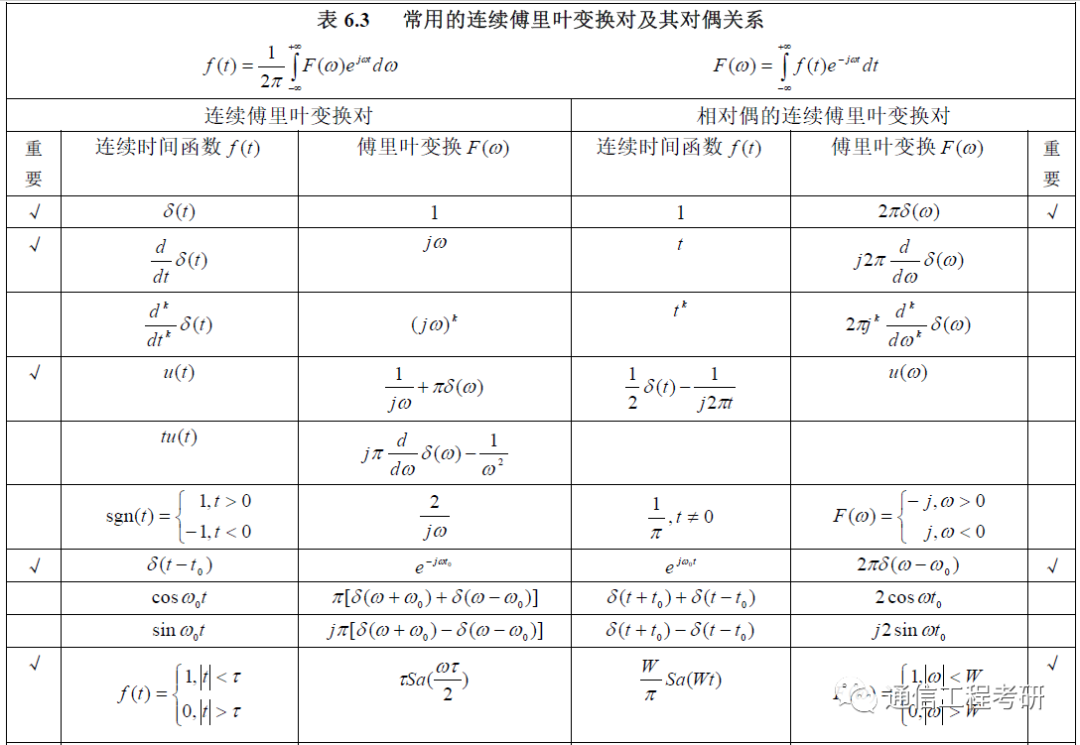
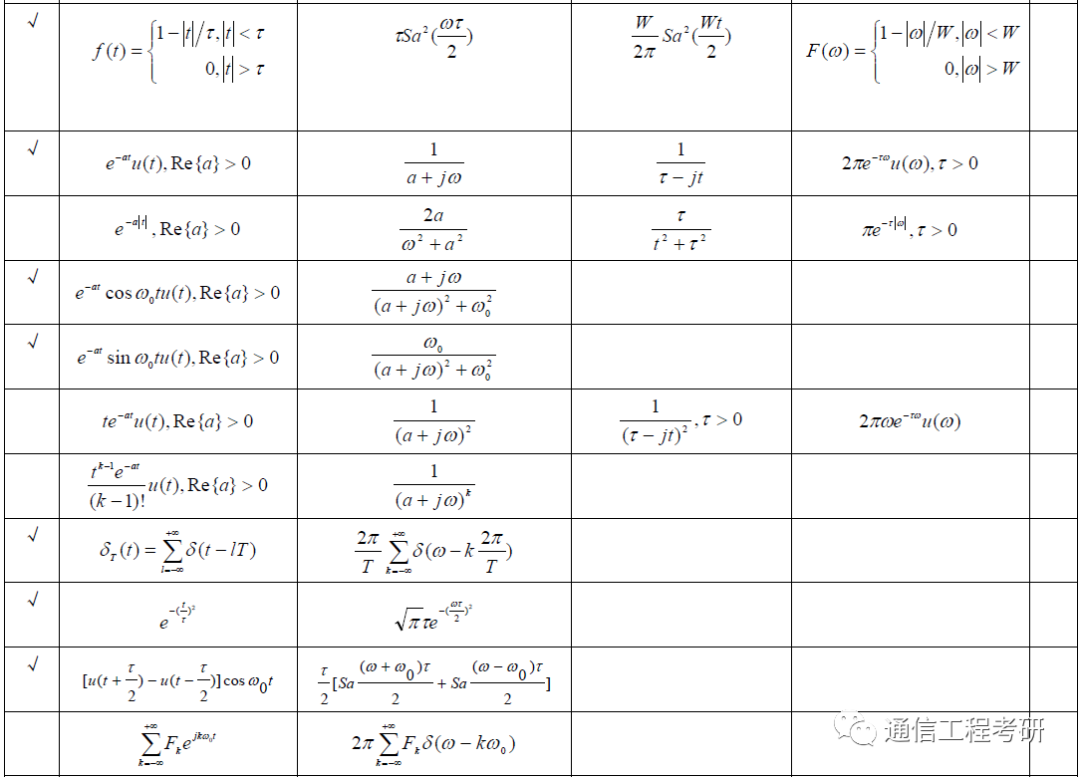
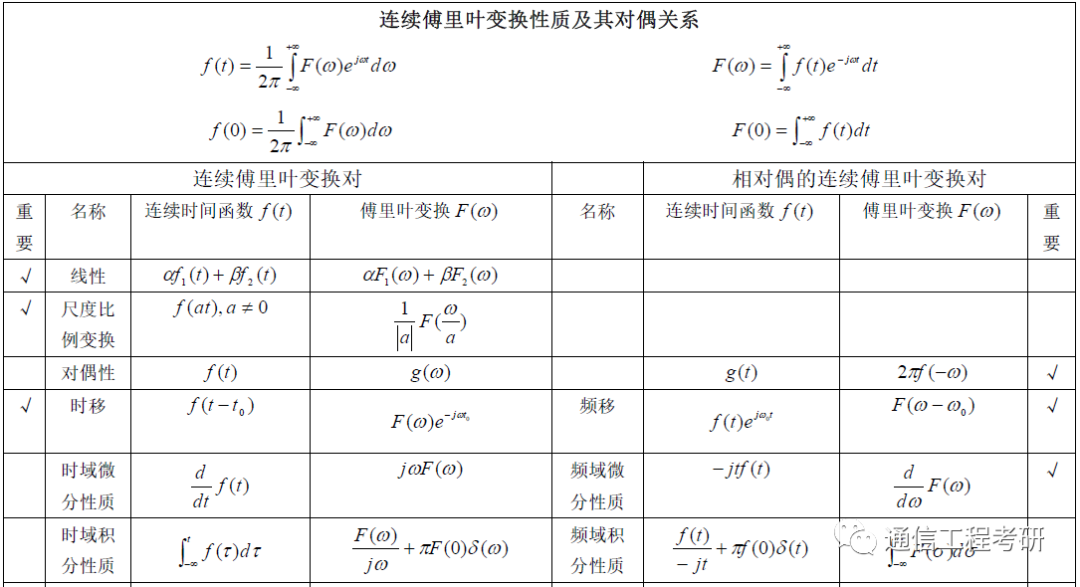
文档地址：链接: https://pan.baidu.com/s/1fJGzfBL4I4s2MMJZA-BZgA 提取码: 8abw