时间序列——SARIMA（气温预测）

数据来源
https://download.youkuaiyun.com/download/weixin_39777626/11800834
到入库&&函数定义

import numpy as np 
import pandas as pd 
import matplotlib.pyplot as plt
import seaborn as sns
import statsmodels.api as sm
from statsmodels.tsa.stattools import adfuller
from statsmodels.graphics.tsaplots import plot_acf, plot_pacf
from sklearn.metrics import mean_squared_error
from math import sqrt
import warnings
warnings.filterwarnings('ignore')
%matplotlib inline

cities = pd.read_csv('F:\paper\dataset\csv\GlobalLandTemperaturesByCity.csv')
countrys = pd.read_csv('F:\paper\dataset\csv\GlobalLandTemperaturesByCountry.csv')

def measure_rmse(y_true, y_pred):
    return sqrt(mean_squared_error(y_true,y_pred))

def check_stationarity(y, lags_plots=48, figsize=(22,8)):
    "Use Series as parameter"
    
    # Creating plots of the DF
    y = pd.Series(y)
    fig = plt.figure()

    ax1 = plt.subplot2grid((3, 3), (0, 0), colspan=2)
    ax2 = plt.subplot2grid((3, 3), (1, 0))
    ax3 = plt.subplot2grid((3, 3), (1, 1))
    ax4 = plt.subplot2grid((3, 3), (2, 0), colspan=2)

    y.plot(ax=ax1, figsize=figsize)
    ax1.set_title('{} Temperature Variation'.format(name))
    plot_acf(y, lags=lags_plots, zero=False, ax=ax2);
    plot_pacf(y, lags=lags_plots, zero=False, ax=ax3);
    sns.distplot(y, bins=int(sqrt(len(y))), ax=ax4)
    ax4.set_title('Distribution Chart')

    plt.tight_layout()
    
    print('Results of Dickey-Fuller Test:')
    adfinput = adfuller(y)
    adftest = pd.Series(adfinput[0:4], index=['Test Statistic','p-value','Lags Used','Number of Observations Used'])
    adftest = round(adftest,4)
    
    for key, value in adfinput[4].items():
        adftest["Critical Value (%s)"%key] = value.round(4)
        
    print(adftest)
    
    if adftest[0].round(2) < adftest[5].round(2):
        print('\nThe Test Statistics is lower than the Critical Value of 5%.\nThe serie seems to be stationary')
    else:
        print("\nThe Test Statistics is higher than the Critical Value of 5%.\nThe serie isn't stationary")

def walk_forward(training_set, validation_set, params):
    '''
    Params: it's a tuple where you put together the following SARIMA parameters: ((pdq), (PDQS), trend)
    '''
    history = [x for x in training_set.values]
    prediction = list()
    
    # Using the SARIMA parameters and fitting the data
    pdq, PDQS, trend = params

    #Forecasting one period ahead in the validation set
    for week in range(len(validation_set)):
        model = sm.tsa.statespace.SARIMAX(history, order=pdq, seasonal_order=PDQS, trend=trend)
        result = model.fit(disp=False)
        yhat = result.predict(start=len(history), end=len(history))
        prediction.append(yhat[0])
        history.append(validation_set[week])
        
    return prediction

def plot_error(data, figsize=(20,8)):
    '''
    There must have 3 columns following this order: Temperature, Prediction, Error
    '''
    plt.figure(figsize=figsize)
    ax1 = plt.subplot2grid((2,2), (0,0))
    ax2 = plt.subplot2grid((2,2), (0,1))
    ax3 = plt.subplot2grid((2,2), (1,0))
    ax4 = plt.subplot2grid((2,2), (1,1))
    
    #Plotting the Current and Predicted values
    ax1.plot(data.iloc[:,0:2])
    ax1.legend(['Real','Pred'])
    ax1.set_title('Current and Predicted Values')
    
    # Residual vs Predicted values
    ax2.scatter(data.iloc[:,1], data.iloc[:,2])
    ax2.set_xlabel('Predicted Values')
    ax2.set_ylabel('Errors')
    ax2.set_title('Errors versus Predicted Values')
    
    ## QQ Plot of the residual
    sm.graphics.qqplot(data.iloc[:,2], line='r', ax=ax3)
    
    # Autocorrelation plot of the residual
    plot_acf(data.iloc[:,2], lags=(len(data.iloc[:,2])-1),zero=False, ax=ax4)
    plt.tight_layout()
    plt.show()
    
tropic=['Madagascar','Bamako','Cairo','Bangkok']
subtropic=['Rome','Xiamen','Argentina','Iraq']
temperate=['London','Peking','New York','Lanzhou']
subfrigid=['Novosibirsk']
frigid=['Greenland','Anchorage']
plateau=['Xining']
climate=[tropic,subtropic,temperate,subfrigid,frigid,plateau]

def sarima(i):
    name=i
    try:
        area=cities.groupby('City').get_group('%s'%i)
        data = cities.loc[cities['City'] == name, ['dt','AverageTemperature']]
    except:
        try:
            area=countrys.groupby('Country').get_group('%s'%i)
            data = countrys.loc[countrys['Country'] == name, ['dt','AverageTemperature']]
        except:
            area=cities.groupby('Country').get_group('%s'%i)
            data = cities.loc[cities['Country'] == name, ['dt','AverageTemperature']]

    data.columns = ['Date','Temp']
    data['Date'] = pd.to_datetime(data['Date'])
    data.reset_index(drop=True, inplace=True)
    data.set_index('Date', inplace=True)

    #I'm going to consider the temperature just from 1900 until the end of 2012
    data = data.loc['1900':'2013-01-01']

    plt.figure(figsize=(22,6))
    sns.lineplot(x=data.index, y=data['Temp'])
    plt.title('Temperature Variation in {} from 1900 until 2012'.format(name))
    plt.show()

    data['month'] = data.index.month
    data['year'] = data.index.year
    pivot = pd.pivot_table(data, values='Temp', index='month', columns='year', aggfunc='mean')
    pivot.plot(figsize=(20,6))
    plt.title('Yearly {} temperatures'.format(name))
    plt.xlabel('Months')
    plt.ylabel('Temperatures')
    plt.xticks([x for x in range(1,13)])
    plt.legend().remove()
    plt.show()

    monthly_seasonality = pivot.mean(axis=1)
    monthly_seasonality.plot(figsize=(20,6))
    plt.title('Monthly Temperatures in {}'.format(name))
    plt.xlabel('Months')
    plt.ylabel('Temperature')
    plt.xticks([x for x in range(1,13)])
    plt.show()

    year_avg = pd.pivot_table(data, values='Temp', index='year', aggfunc='mean')
    year_avg['10 Years MA'] = year_avg['Temp'].rolling(10).mean()
    year_avg[['Temp','10 Years MA']].plot(figsize=(20,6))
    plt.title('Yearly AVG Temperatures in {}'.format(name))
    plt.xlabel('Months')
    plt.ylabel('Temperature')
    plt.xticks([x for x in range(1900,2017,3)])
    plt.show()

    train = data[:-60].copy()
    val = data[-60:-12].copy()
    test = data[-12:].copy()

    # Excluding the first line, as it has NaN values
    baseline = val['Temp'].shift()
    baseline.dropna(inplace=True)

    rmse_base = measure_rmse(val.iloc[1:,0],baseline)
    print(f'The RMSE of the baseline that we will try to diminish is {round(rmse_base,4)} celsius degrees')

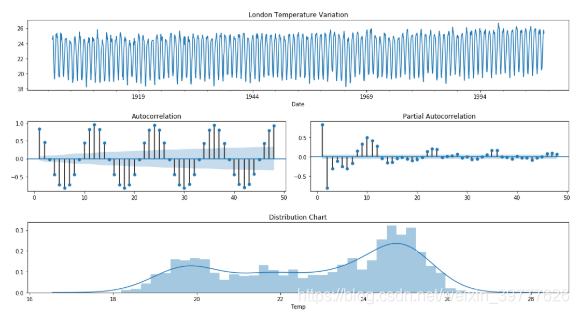
    check_stationarity(train['Temp'])

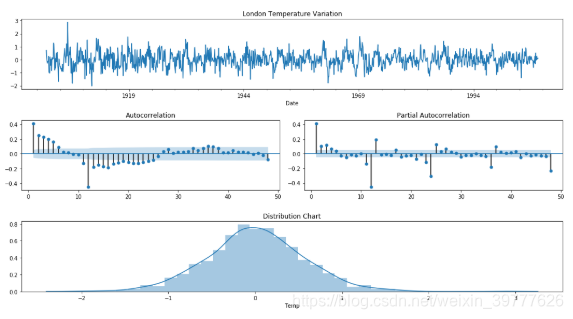
    check_stationarity(train['Temp'].diff(12).dropna())

    if name=='Madagascar' or name=='Bamako' or name=='Bangkok' or name=='Xining':
        val['Pred'] = walk_forward(train['Temp'], val['Temp'], ((2,0,0),(0,1,1,12),'c'))
    else:
        val['Pred'] = walk_forward(train['Temp'], val['Temp'], ((3,0,0),(0,1,1,12),'c'))

    rmse_pred = measure_rmse(val['Temp'], val['Pred'])

    print(f"The RMSE of the SARIMA(3,0,0),(0,1,1,12),'c' model was {round(rmse_pred,4)} celsius degrees")
    print(f"It's a decrease of {round((rmse_pred/rmse_base-1)*100,2)}% in the RMSE")

    val['Error'] = val['Temp'] - val['Pred']

    val.drop(['month','year'], axis=1, inplace=True)

    plot_error(val)

    future = pd.concat([train['Temp'], val['Temp']])

    model = sm.tsa.statespace.SARIMAX(future, order=(3,0,0), seasonal_order=(0,1,1,12), trend='c')
    result = model.fit(disp=False)

    test['Pred'] = result.predict(start=(len(future)), end=(len(future)+13))

    test[['Temp', 'Pred']].plot(figsize=(22,6))
    plt.title('Current Values compared to the Extrapolated Ones')
    plt.show()

    test_baseline = test['Temp'].shift()

    test_baseline[0] = test['Temp'][0]

    rmse_test_base = measure_rmse(test['Temp'],test_baseline)
    rmse_test_extrap = measure_rmse(test['Temp'], test['Pred'])

    print(f'The baseline RMSE for the test baseline was {round(rmse_test_base,2)} celsius degrees')
    print(f'The baseline RMSE for the test extrapolation was {round(rmse_test_extrap,2)} celsius degrees')
    print(f'That is an improvement of {-round((rmse_test_extrap/rmse_test_base-1)*100,2)}%')
    print('--------------------------{}--------------------------------'.format(name))

调用函数（输入城市、国家名称）

sarima('Madagascar')

部分结果展示
详细分析。。。。以后有空再说吧。。

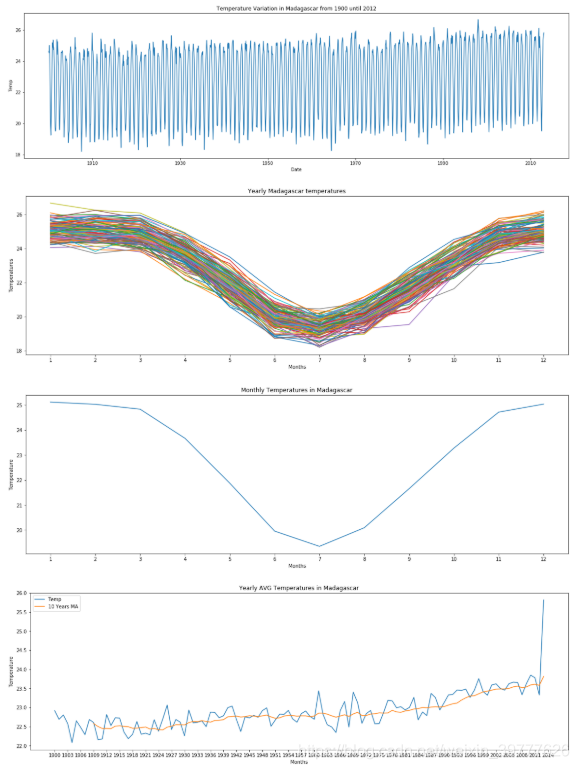
The RMSE of the baseline that we will try to diminish is 1.2276 celsius degrees
Results of Dickey-Fuller Test:
Test Statistic -2.2666
p-value 0.1830
Lags Used 23.0000
Number of Observations Used 1273.0000
Critical Value (1%) -3.4355
Critical Value (5%) -2.8638
Critical Value (10%) -2.5680
dtype: float64

The Test Statistics is higher than the Critical Value of 5%.
The serie isn’t stationary
Results of Dickey-Fuller Test:
Test Statistic -14.0939
p-value 0.0000
Lags Used 23.0000
Number of Observations Used 1261.0000
Critical Value (1%) -3.4355
Critical Value (5%) -2.8638
Critical Value (10%) -2.5680
dtype: float64

The Test Statistics is lower than the Critical Value of 5%.
The serie seems to be stationary
The RMSE of the SARIMA(3,0,0),(0,1,1,12),‘c’ model was 0.3652 celsius degrees
It’s a decrease of -70.25% in the RMSE



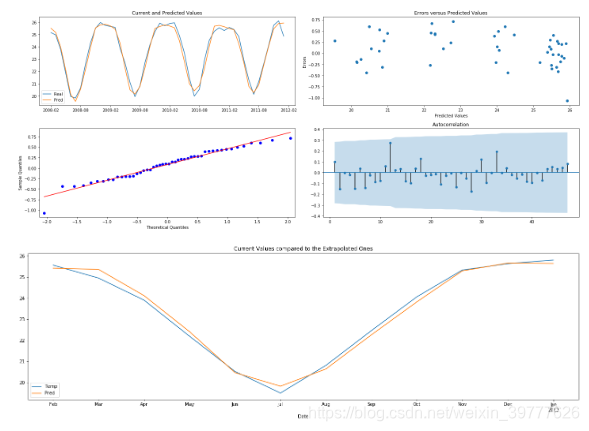
The baseline RMSE for the test baseline was 1.19 celsius degrees
The baseline RMSE for the test extrapolation was 0.21 celsius degrees
That is an improvement of 82.04%
--------------------------Madagascar--------------------------------