前言
这两天刷数分、高代题(虽然我开学大四,但因一些情况,我需要gap一年才会考研,今年不考,所以有时间做点闲题~~)。 发现一个用反常积分+极限的方式,可以计算一个函数的极限。题中的条件令我突然想到之前机器学习课里,讲一些边缘检测的内容。各种各样卷积核,什么Laplace算子、Gauss-Laplace算子。将灰度处理后的图片看作是一个地形图,那么边缘便是地形起伏较大的区域。
再想到对求导定义的理解,倘若对
最后,这篇文章属于偏向数学的。但我又想把这种理解——“积分-微分-边缘检测”这个整体给表述出来。谈的有点多、杂,奈何学识有限,有些地方理解/表达不是那么准确,望指出。
大致内容:从积分角度进入,通过一些积分的特殊结果引出求导,给出一些代数角度的理解。最后简单说说关于边缘检测中的理解。
目录
- 铺垫积分的内容
- 主观能动性的体现——视积分为具有某性质的作用
- 从代数角度来看微分
- 二元离散情形
铺垫积分的内容
这里我打算先给出我对“定积分”算子意义上的理解,以便于后面继续探讨~
有句话说得好,
割之弥细,所失弥少,割之又割以至于不可割,则与圆合体而无所失矣——刘徽。
对于积分,可以理解是一种“连续指标”下的求和,换做一种向量的视角下
陆艺:聊一聊【向量】视角下的函数(例子:傅里叶变换)zhuanlan.zhihu.com
(该文意在抛出一种 向量-函数 的观念)
就是一个向量,与某个数量向量的内积了,即对于积分
当然,这些讨论的是Riemann积分,其实Riemann积分还可以看作是对函数的“条形图”求面积。
那Lebesgue积分呢?其实就是对函数的“直方图”求面积啦。
Riemann求积分的过程显然是个按”数组“顺序求和的过程,但是Lebesgue积分,更像按照dict这个类型求和(注:dict为python中的一种数据类型,键对应值,而键不具有顺序。)
好,铺垫到此为止,下面说说关于积分的玩法~
主观能动性的体现——视积分为具有某性质的作用
高中时,我们都学过哲学(不是哲♂学)。其中,里面有句话说:“人区别于其他物的表现在于人具有主观能动性”。
如果要通过“积分”来体现出主观能动性的话,仅停留于表面还是不行的(背个定义、考个期末),还需要对“积分”有更加深刻的理解才行。当然 ,胡思乱想、乱用概念也是夸大了“主观能动性”的作用(改编不是乱编,戏说不是胡说)。
所以,咱们首先需要知道积分能有哪些”高级“性质(一般教科书上的线性性质、两个中值定理还有不等式关系这里暂且不谈,因为和主题关系不大)。下面,通过几道题来观察它的”高级“性质(题目比较简单涉及证明的地方可以自行忽略,即“证明:......QED”之间的内容)。
这道题,先摆出来证明过程,再说背后原理。
例 设在
上连续,则有:
证明:
通过计算发现
QED
其实,对于这种定积分参数带极限的问题,就拿这题来说,可以做如下的思考。
将变量进行替换,再做一步整理
然后,通过简单画出相应的示意图,则有
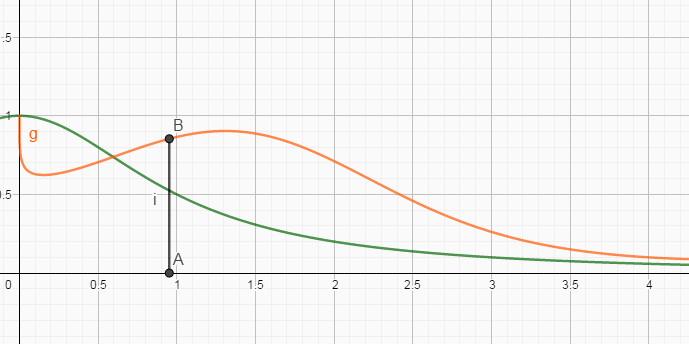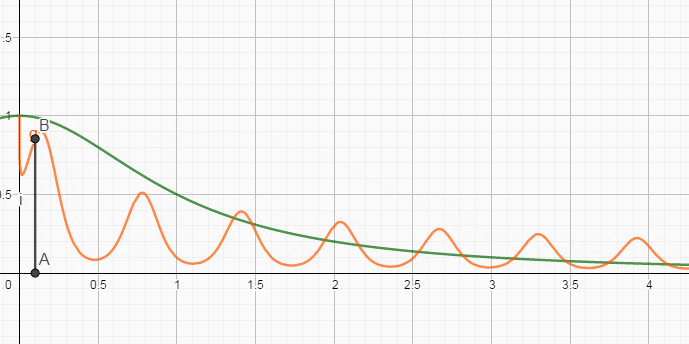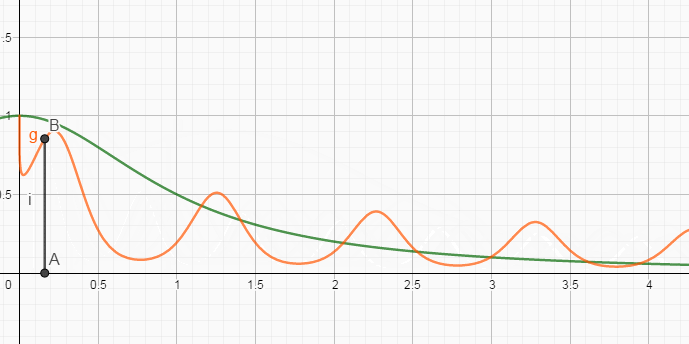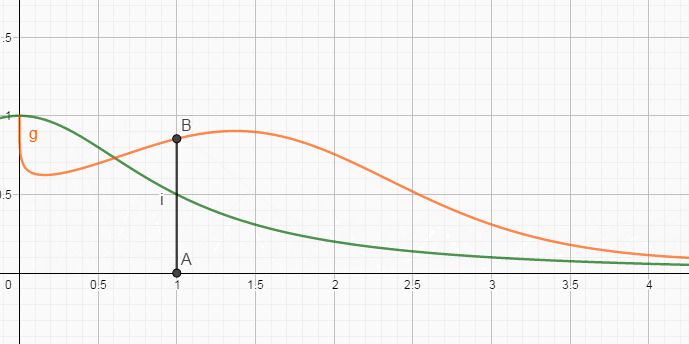
能发现,随着
假设,在
也就是说,当
最终结果,就是:”取函数的0处的值,并扩大了
同样的一些问题还有几个,我先列出来,证明的内在思路是差不多的,表述上会有所不同,这里就不再去细讲了。
例 设在
上可积,
,
是
周期的函数,在为
上可积,则有
按照上面所讲的,可以想成把
例(Riemann-Lebesgue引理) 若在
上可积,
是
周期的函数,在为
上可积,则
这里
例 若在
上可积,
是
为周期的函数,在
上可积,则
该命题可以看作是上一个命题的推广,不过极限是针对于实数的。证明上可以先:有理数成立
例(Riemann定理) 若在
上绝对可积,
是
为周期的函数,在
上可积,则
证明上,借助上一命题,只需要考虑积分区间足够大之外的部分即可。
从上面这些,可以看出,在区间上对某一个函数进行积分可以记为
所以,对于第一个例子,可以看成
(充当泛函的作用~)
下面,是我特别想要说的,就是用积分来表示求导:
例 设为
上连续的函数,如果该函数满足
设
是
上可微函数,则
证明:
通过替换变量,等式左边可以成为
然后往导数方向凑凑 ,根据
成立。那它为什么成立呢?
因为
所以,这种积分变换,可以用符号
(令
从代数角度来看微分
先提两个概念,一个是线性空间,一个是线性映射。
要知道数学中,最原始的概念应该是集合,所谓空间、代数、格、模、域、环还有群,都是在集合上不断添加性质猜得到的。正所谓:“世上本无路,有了腿才有了路”~
对于域上线性空间就是对两个封闭运算(加法、数乘)满足:加法交换、结合,含有幺元、零元、加法逆元;数乘上,满足”一数分配两个向量“、”两数之和分配一个向量 、“一次数乘可分成两数先后相乘“。
于是乎,
- 几何空间中所有以原点为起点所有向量组成的几何,对于向量加法和数量乘法成为
上的一个线性空间。
- 域
上所有
元有序组组成的集合
,对于矩阵的加法与数量乘法,成为域
上的一个线性空间,称为域
的
维线性空间。
- 数域
上矩阵组成集合
- 多项式组成的集合
(可以限制次数小于
)
- 复数域
- 所有
到
上的函数
当一个集合里的元素,满足线性性质的时候,就可以通过“基(base)”来表达任意一个点了,而且是唯一的。如果基有限,那么只需要研究好基就能挖掘好空间性质。
对于空间的表示,既然是具备线性性质了,那么也可以用一根一根的线来表达:
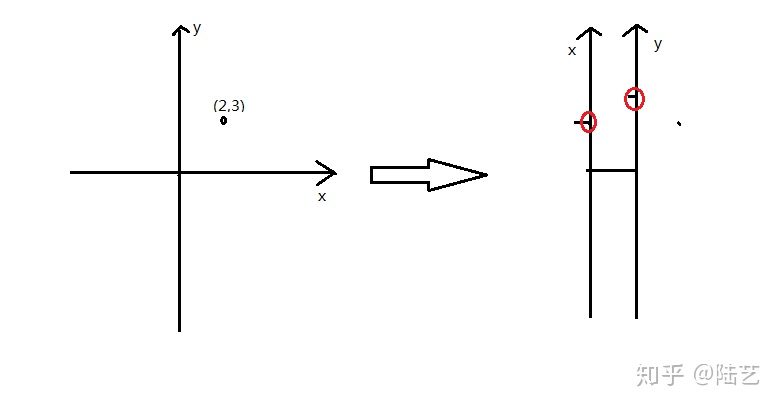
对于线性映射与线性变换,是指具有齐次性和可加性的映射,前者一般表示从一种空间到另一种空间映射,后者指空间到自身的映射。就好像:一张纸烧成灰与一张纸变成纸飞机的区别。
在数学分析中,有个东西角泰勒展开,将一个函数,在局部意义下写成一个多项式的情形。将超过某一个
所以不妨先来看看多项式空间
对于基为
于是,用矩阵表示该算子即为
发现,这也是个主对角全部为0的Jordan块,所以幂零指数为
当然,对于不同的基,微分算子的矩阵表示也会有所不同,这里就不多去叙述。
对于一元函数的线性表示——向量,来做求导, 这个算子是可以的。
那么对于二元函数——矩阵,这个怎么求导呢?
二元离散情形
一般的卷积定义为
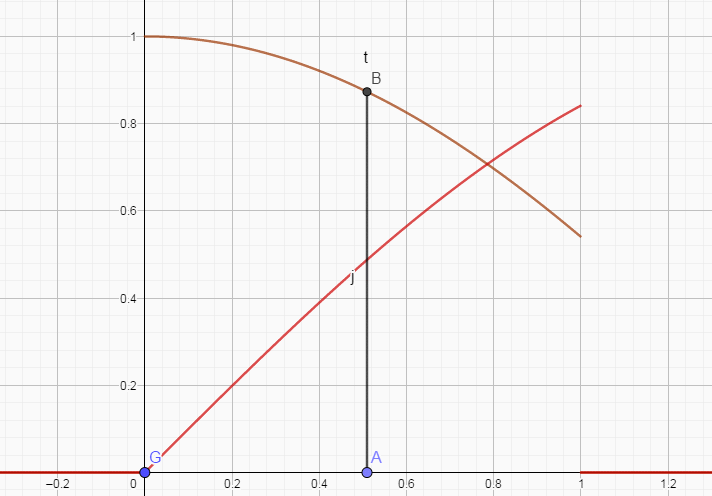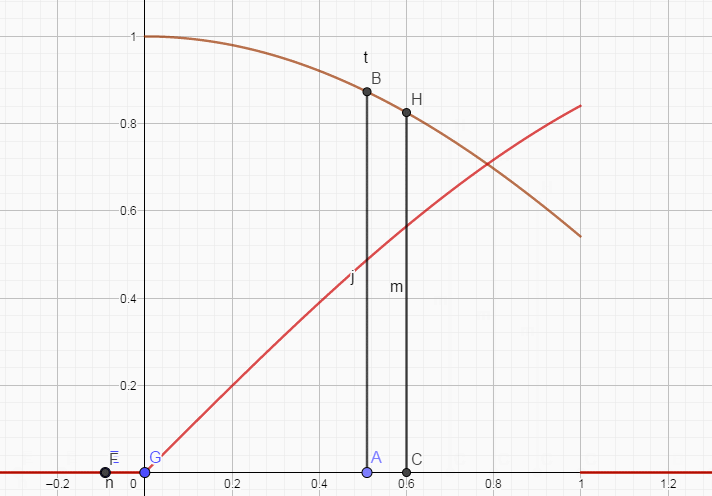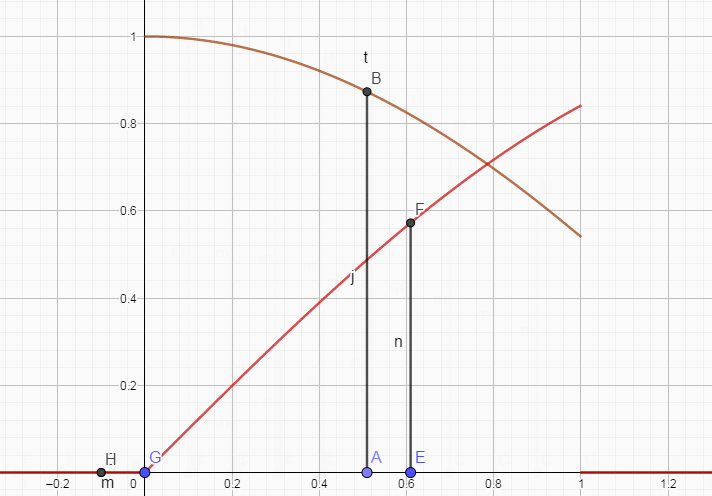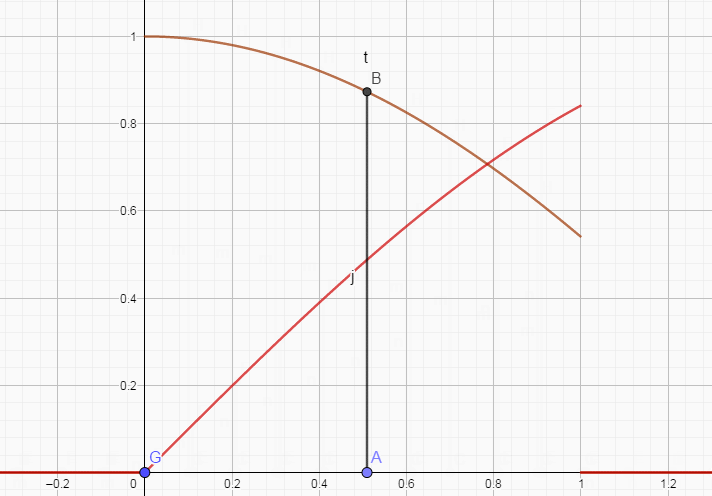
离散的情形就是
相应的
用一个二元函数来表示某一张图,
当变量超过原像(可以看成有限点组成的格)的时候,按零来处理。
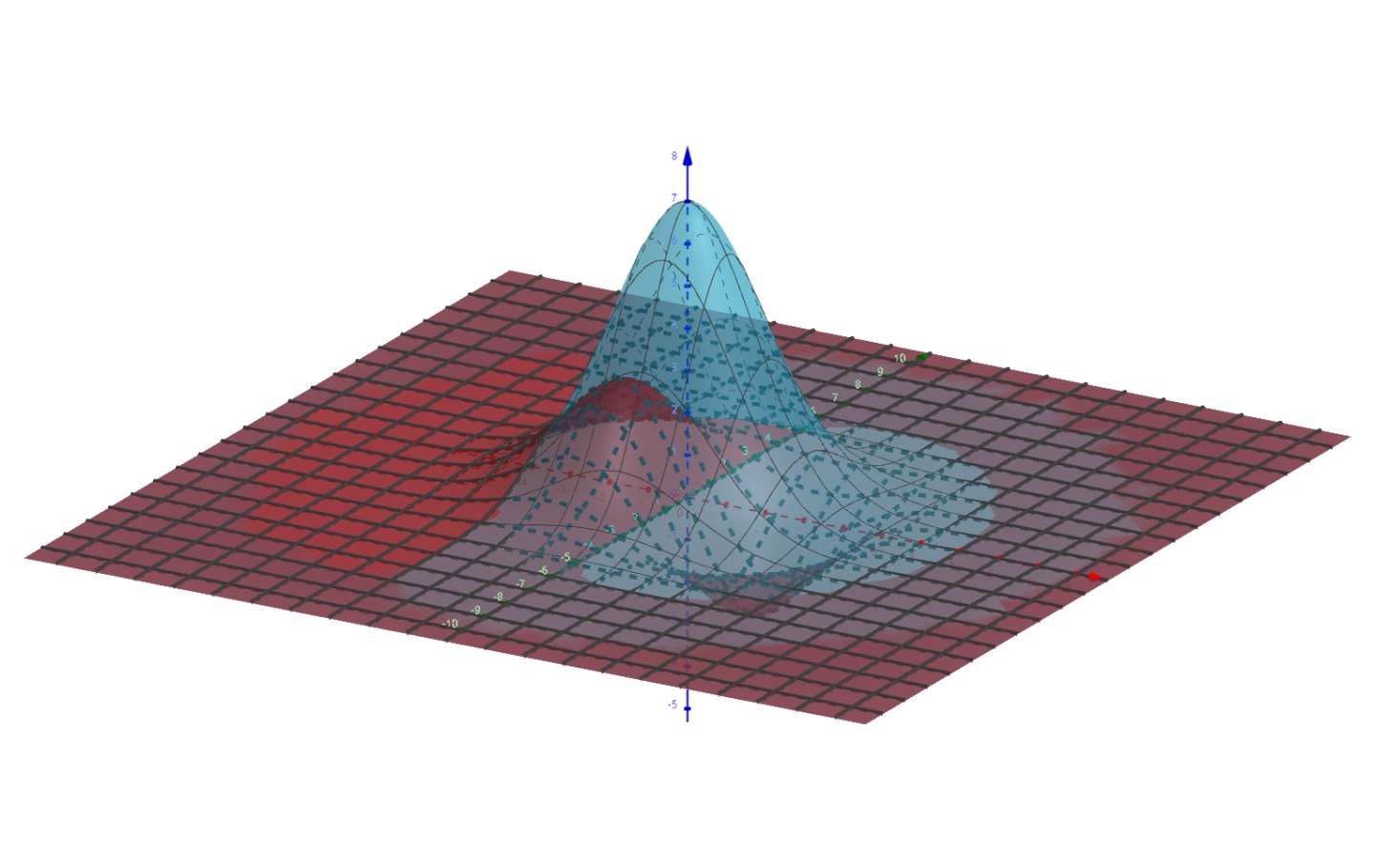
对于这篇文章的封面,画成图,即
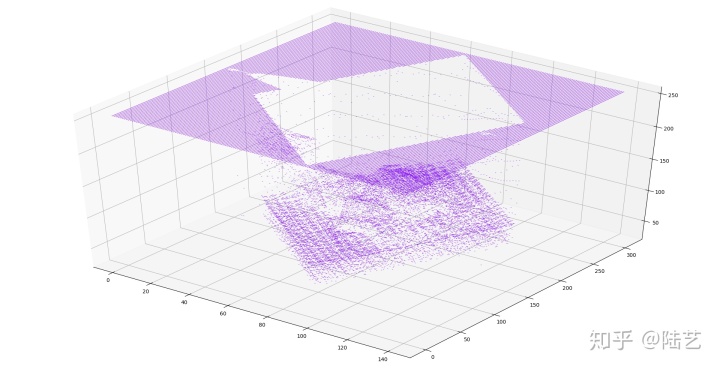
回顾之前所说的用积分定义的求导
设为
上连续的函数,如果该函数满足
设
是
上可微函数,则
能发现,这两个矩阵
关于这种检测的实验结果,可以搜索其他人的文章(边缘检测)即可。







 本文探讨了积分与微分在边缘检测中的应用,通过数学分析引入了一种利用积分定义求导的方法,并将其应用于图像处理中,实现了对图像边缘的有效检测。
本文探讨了积分与微分在边缘检测中的应用,通过数学分析引入了一种利用积分定义求导的方法,并将其应用于图像处理中,实现了对图像边缘的有效检测。

















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








