非线性薛定谔方程_分步傅里叶法求解非线性薛定谔方程（二）

最新推荐文章于 2025-05-13 01:03:36 发布
最新推荐文章于 2025-05-13 01:03:36 发布
阅读量1.3w 收藏 84
点赞数 21
文章标签： 非线性薛定谔方程
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.youkuaiyun.com/weixin_39768083/article/details/111335383
版权
本文介绍了利用MATLAB进行非线性薛定谔方程(NLSE)的分步傅里叶法求解仿真，探讨了在不同参数下，如色散、非线性、衰减对光脉冲传播的影响。通过仿真展示了非线性如何补偿色散导致的脉冲宽度展宽，并讨论了模式色散、波导色散等光纤中色散类型及非线性效应如自相位调制。

摘要生成于 C知道 ，由 DeepSeek-R1 满血版支持， 前往体验 >

关于非线性薛定谔方程(NLSE)的求解方法主要包括有限差分法和伪谱法。在上回介绍NLSE时笔者介绍了利用伪谱法即有限傅里叶变换方法求解时，需要特别考虑的几个参数进行了介绍，笔者这回主要介绍利用MATLAB仿真的方式将利用分步傅里叶法求解NLSE进行仿真介绍。

典型的NLSE方程可以表示为如下形式，其中包含了光脉冲传播时的衰减项、色散项和非线性项。

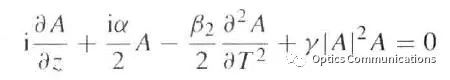
38757ba0218049139acd3be83cf1a43b.png

通过改变仿真时的参数，来观察色散、非线性、衰减等参数来观察光脉冲在光纤中传播时的影响。

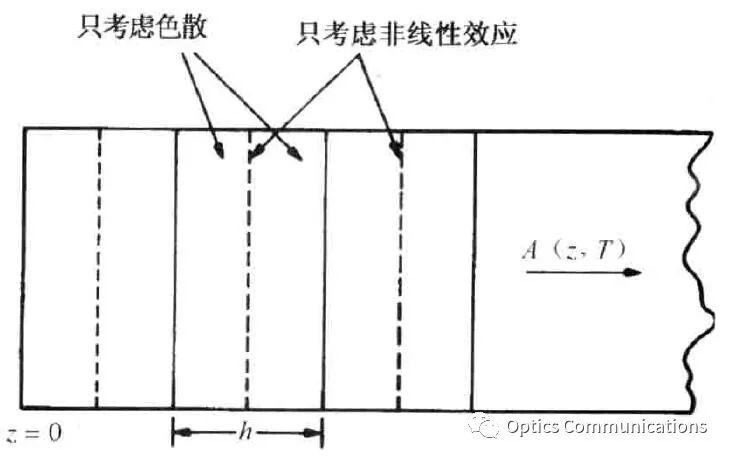
ad95b3cebc6a5031a279a796a55b3544.png

本仿真在编写软件代码时，以《Nonlinear Fiber Optics-Fifth Edition》中提供的参考代码为原型，根据仿真需要对代码进行增删修改。

在忽略损耗的前提下，不考虑非线性作用，只考虑色散项时，NLSE可以化简为：

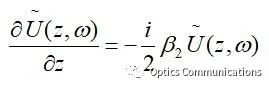
177fd88064798cd0e48f10ffa5f48ba4.png

求

最低0.47元/天 解锁文章
分步傅里叶算法_分布傅里叶算法求解非线性薛定谔的matlab程序问题
weixin_42510567的博客
12-31 3221
[size=14.399999618530273px]分布傅里叶算法求解非线性薛定谔的matlab程序里，我注释的可能也有错误，请指导@alpha=0;%光纤损耗值，单位dB/kmalph=alpha/(4.343);%光纤损耗值，单位dB/kmgamma=0.003;%光纤非线性参数to=125e-12;%初始脉冲宽度，单位秒C=-2;%第一次计算输入的啁啾参数@b2=-20...
线性与非线性调制的薛定谔方程求解
m0_74043383的博客
05-26 832
线性调制薛定谔方程求解； 非线性调制薛定谔方程求解； 以及线性与非线性调制薛定谔方程求解
非线性薛定谔方程的求解-讲义 复变函数论
08-16
非线性薛定谔方程的求解-讲义 复变函数论的理论深化 想对复变函数进行深入研究的同学不妨看一下
求解非线性薛定谔方程的几种方法：引领光纤通信技术新篇章
最新发布
gitblog_06789的博客
05-13 285
求解非线性薛定谔方程的几种方法：引领光纤通信技术新篇章 【下载地址】求解非线性薛定谔方程的几种方法 该项目聚焦于非线性薛定谔方程的求解方法，为光纤通信系统中光孤子传输的研究提供有力支持。通过系统整理和比较Jacobi椭圆函数展开法、三角函数假设法、试探函数法以及(G′/G)展开法等几种典型方法，项目深入剖析了各方法的优劣...
分步傅里叶方法求解非线性薛定谔方程 SSFM
08-26
分步傅里叶方法求解非线性薛定谔方程的matlab代码，可以很精准的仿真光脉冲在光纤信道中的传输
分布傅里叶变换解非线性薛定谔方程
06-02
分布傅里叶变换解非线性薛定谔方程，非线性光纤光学数值计算
分步傅里叶算法_分步傅里叶法求解非线性薛定谔方程的改进及其数值计算
weixin_42297347的博客
02-05 1699
【1】J. Herrera, F. Ramos, J. Marti. Small-signal analysis of wavelength converters based on cross-phase modulation in dispersion-shifted fibers［J］. IEEE Photon. Technol. Lett., 2005, 17(11): 2370～2372【...
分步傅里叶法求解非线性薛定谔方程的改进及其数值计算
02-25
在分步傅里叶法求解非线性薛定谔方程的基础上，介绍了一种时间窗口和步长动态自适应调整的改进算法，该算法根据时域脉冲的扩散情况调整时间窗口，采用局部误差法控制计算步长，在保证精度的同时提高了计算效率。讨论了数值计算时如何正确选取正、逆傅里叶变换的形式，分析了如何由离散的计算结果近似连续的时域和频域波形。模拟了光子晶体光纤中超连续谱的产生，验证了算法的正确性。
47456753split_step_fourier_method_非线性薛定谔方程_分布傅里叶_
09-30
在求解非线性薛定谔方程时，这种方法通常采用Split-Step Fourier Technique，即分步傅里叶法。这种技术将整个演化过程分为两步：第一步是进行傅里叶变换，处理非线性项；第二步是进行反傅里叶变换，处理线性项。通过...
soliton.rar_split step_split step method_分步傅里叶_薛定谔方程_非线性薛定谔
07-15
总之，"soliton.rar_split step_split step method_分步傅里叶_薛定谔方程_非线性薛定谔"是一个使用MATLAB实现的非线性薛定谔方程的分步傅里叶算法求解器。通过对提供的MATLAB代码进行分析和运行，我们可以深入理解...
光孤子传播过程 非线性薛定谔方程_光纤激光_激光传输_光孤子传输_光纤激光器_光孤子_源码
10-04
这些代码可能使用了数值方法，如分步傅里叶法，来求解非线性薛定谔方程，帮助科研人员理解和预测光孤子的行为。 通过对这些知识点的深入理解和应用，科学家和工程师能够设计更高效的光纤激光器，优化光孤子传输系统...
光纤 分步傅里叶法 非线性薛定谔方程
06-11
光纤中利用分步傅里叶法对非线性薛定谔方程进行仿真
非线性薛定谔方程（光）
08-13
光脉冲经过一段光纤后的表达式 This function solves the nonlinear Schrodinger equation for pulse propagation in an optical fiber using the split-step Fourier method. The following effects are included in the model: group velocity dispersion (GVD), higher order dispersion, loss, and self-phase modulation (gamma).
非线性薛定谔方程数值解的MATLAB仿真
11-15
文档推理加程序，非线性薛定谔方程数值解的MATLAB仿真
非线性薛定谔方程求解代码
05-16
求解非线性薛定谔方程的求解代码，个人感觉挺好的~~分享给大家
非线性薛定谔方程_五分钟彻底搞懂“薛定谔方程”
weixin_39587822的博客
12-14 6498
微观世界里面有几个奇特的现象，那就是微观世界具有“不确定性”，但是同时我们也知道不确定不等于不可研究，也不等于无规律，因为微观的“不确定”特点恰好就是微观世界的规律，所以我们只要掌握住了这个规律，一样可以研究微观世界来为人类服务，这个规律我们如何描述呢？那就是薛定谔方程。可以这么说，牛顿定律在宏观世界里几乎是无所不能，那么“薛定谔方程”就是微观世界的“牛顿力学”，只不过微观世界一般人不会...
有偿求分布傅里叶法解非线性薛定谔方程
weixin_69489271的博客
05-16 273
求一个分布傅里叶数值解非局域非线性薛定谔方程的代码，要传输空间光的，线性项是衍射和非线性项是自聚焦的，不是传输脉冲。
基于分步傅立叶数值算法的一维非线性薛定谔方程求解matlab仿真
熟悉python,matlab,C,C++,JAVA等
06-01 2319
分步傅立叶法是一种有效且广泛应用于求解 NLSE 的数值方法，它将非线性和扩散部分分开处理，利用傅立叶变换高效地求解线性部分。其基本思想是将时间演化分成小的时间步长Δt，并在每个时间步内，先线性地处理波动项（即施加傅立叶变换处理扩散），然后处理非线性项。另外，从上面的式子可以看到，整个方程中U只和Z和T相关，其余均为常系数，或者是变常系数，但这U无关，那么我们简化上面的公式，把我们的公式变为标准非线性薛定谔的表现形式。从对比可知，这两个式子形式上是相同的，区别在于本课题的式子在标准式子基础上增加了系数。
QQmlComponent: Component is not ready 是什么原因？如何解决？
10-30
QQmlComponent: Component is not ready 是Qt Quick（一种用于构建用户界面的框架）中的一个常见错误，它表示你试图在组件（Component）还没有完全加载完成或者初始化完毕的时候就去使用它。这通常是由于以下几个原因： 1. **生命周期问题**：如果你在组件实例化之前就尝试访问它的属性或调用方法，就会遇到这种错误。你需要确保在`onCompleted`信号触发后再使用组件。 ```qml QQmlComponent component; component.loadUrl(QUrl("path_to_your_qml_file.qml")); component.onCompleted.connect({ // 现在可以安全地使用component了 var instance = component.create(); }); ``` 2. **网络延迟**：如果组件通过网络请求加载，网络未响应或数据加载时间过长，可能导致此错误。确保网络请求已经成功并且数据已准备好。 3. **资源依赖**：有些组件依赖于其他资源（如图像、音频等），如果没有正确设置或者加载顺序不对，也可能引发此错误。确认资源是否都已加载，并按正确的顺序初始化。 4. **构造函数问题**：如果你在构造函数中进行了复杂的操作，可能会阻塞组件的初始化过程。尽量避免在构造函数中做耗时的操作。 解决这个问题的关键在于理解组件的生命周期，并确保在其真正准备就绪后进行交互。你可以使用`onCompleted`信号或`isReady`属性来确保这一点。
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值