无人驾驶路径规划的卡尔曼滤波的使用——卡尔曼滤波的实现步骤

1、应用简介
kalman滤波在状态估计和多传感器融合等方面应用广泛，典型的应用有无人机的飞行姿态估计，汽车的行驶状态估计，无人驾驶中的激光雷达和其他传感器之间的融合等。
2、算法步骤
（1）表达式
根据现代控制理论，一个线性系统可以被描述为以下形式：
状态方程：
$$\begin{gathered} x_k=A{x}_{k-1}+B{u}_k+w_k \\ {x}_k=A{x}_{k-1}+B{u}_k+w_k \end{gathered}$$
观测方程：
$$\begin{gathered} z_k=H{x}_k+v_k \\ {z}_k=H{x}_k+v_k \end{gathered}$$

其中， w_{k}是过程噪声，服从高斯分布， v_{k}是观测噪声，也服从高斯分布，即：
$$\begin{gathered} p(w)-N(0,Q) \\ p(v)-N(0,R) \end{gathered}$$

Q是过程噪声的协方差，R是观测噪声的协方差。

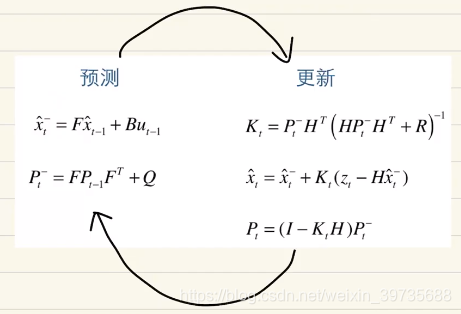
（2）kalman滤波分为预测和更新两步：
1）预测
预测是根据上一时刻的状态量，由系统的微分方程预测下一时刻的系统状态量，并且产生状态量误差协方差的先验估计矩阵P
状态预测：
$${\hat{x}}_k^{-}=A{\hat{x}}_{k-1}+B{u}_k$$

误差协方差矩阵预测：
$$P_k=A{P}_{k-1}{A}^T+Q$$
这里的x̂ {k}^{−} 为先验估计值，P{k}^{−}为先验协方差。
2)更新
状态更新首先根据前面预测的状态量x由观测方程计算出理论上的观测值，然后获得传感器的实际测量值，将这两个值做差，计算出kalman滤波器的增益K，进而校正之前的预测值。同时需要计算后验的误差协方差矩阵P：
增益矩阵：
$$K_k=\frac{P_k{H}^T}{(H{P}_k{H}^T+R)}$$

状态更新：
$${\hat{x}}_k={\hat{x}}_k^{-}+K_k(z_k-H{\hat{x}}_k^{-})$$
其中，z_{k}为测量方程：
$$z_k=H{\hat{x}}_k^{-}+v$$
v为噪声误差。
误差协方差矩阵更新：
$$P_k=(I-K_{k}H)P_k^{-}$$
P_{k}即为后验估计协方差，$I$为对角单位矩阵。
其实Kalman用起来一点儿也不复杂，最主要的是要找到系统的微分方程。然后套用上面的五个核心公式即可。