数据结构(二十一) -- 常用的十种算法(三) -- 动态规划算法

1. 应用场景：背包问题

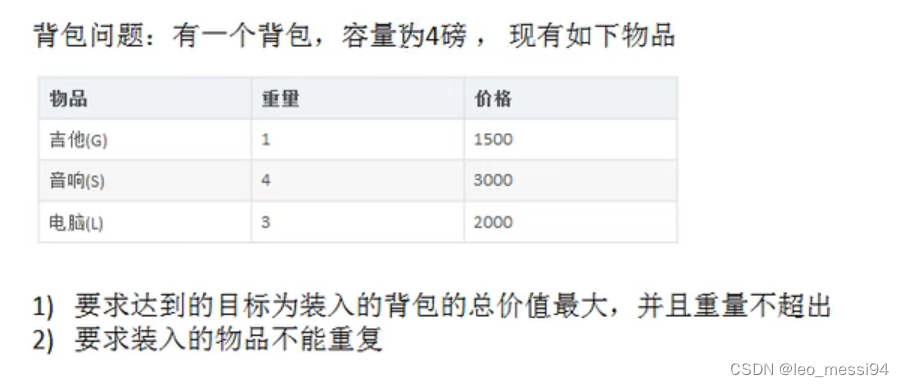
2. 动态规划算法介绍：

3. 动态规划解决背包问题

3.1 思路分析：

其中v[i][j]=max{v[i-1][j],v[i-1][j-w[i]]}中：

• j-w[i]表示：除掉当前商品，剩余的容量
• v[i-1][j-w[i]]表示：除掉当前商品，剩余的i-1商品在剩余容量范围内能够存放的最大价值
• 也就是比较还是按照上个策略得到的价值和按照加入当前商品然后用剩余空间存放最大价值的商品得到的价值的大小。
  • 即比如总重量为7
  • 原来存放三个重量为2价值为1500的东西，此时i=3，v[3][7]=4500
  • 来了第四个商品，重量3价值为2000，此时i=4，v[4][7]=max{4500，v[4] + v[3][4]}，即v[4][7]=max{4500,2000+v[3][4]}

3.2 图解：

3.3 代码：

public class KnapsackProblem {

	public static void main(String[] args) {
		// TODO Auto-generated method stub
		int[] w = {1, 4, 3};//物品的重量
		int[] val = {1500, 3000, 2000}; //物品的价值 这里val[i] 就是前面讲的v[i]
		int m = 4; //背包的容量
		int n = val.length; //物品的个数

		//创建二维数组，
		//v[i][j] 表示在前i个物品中能够装入容量为j的背包中的最大价值
		int[][] v = new int[n+1][m+1];
		//为了记录放入商品的情况，我们定一个二维数组
		int[][] path = new int[n+1][m+1];

		//初始化第一行和第一列, 这里在本程序中，可以不去处理，因为默认就是0
		for(int i = 0; i < v.length; i++) {
			v[i][0] = 0; //将第一列设置为0
		}
		for(int i=0; i < v[0].length; i++) {
			v[0][i] = 0; //将第一行设置0
		}

		//根据前面得到公式来动态规划处理
		for(int i = 1; i < v.length; i++) { //不处理第一行 i是从1开始的
			for(int j=1; j < v[0].length; j++) {//不处理第一列, j是从1开始的
				//公式
				if(w[i-1]> j) { // 因为我们程序i 是从1开始的，因此原来公式中的 w[i] 修改成 w[i-1]
					v[i][j]=v[i-1][j];
				} else {
					//说明:
					//因为我们的i 从1开始的， 因此公式需要调整成
					//v[i][j]=Math.max(v[i-1][j], val[i-1]+v[i-1][j-w[i-1]]);
					//v[i][j] = Math.max(v[i - 1][j], val[i - 1] + v[i - 1][j - w[i - 1]]);
					//为了记录商品存放到背包的情况，我们不能直接的使用上面的公式，需要使用if-else来体现公式
					if(v[i - 1][j] < val[i - 1] + v[i - 1][j - w[i - 1]]) {
						v[i][j] = val[i - 1] + v[i - 1][j - w[i - 1]];
						//把当前的情况记录到path
						path[i][j] = 1;
					} else {
						v[i][j] = v[i - 1][j];
					}

				}
			}
		}

		//输出一下v 看看目前的情况
		for(int i =0; i < v.length;i++) {
			for(int j = 0; j < v[i].length;j++) {
				System.out.print(v[i][j] + " ");
			}
			System.out.println();
		}

		System.out.println("============================");
		//输出最后我们是放入的哪些商品
		//遍历path, 这样输出会把所有的放入情况都得到, 其实我们只需要最后的放入
//		for(int i = 0; i < path.length; i++) {
//			for(int j=0; j < path[i].length; j++) {
//				if(path[i][j] == 1) {
//					System.out.printf("第%d个商品放入到背包\n", i);
//				}
//			}
//		}
		//动脑筋
		int i = path.length - 1; //行的最大下标
		int j = path[0].length - 1;  //列的最大下标
		while(i > 0 && j > 0 ) { //从path的最后开始找
			if(path[i][j] == 1) {
				System.out.printf("第%d个商品放入到背包\n", i);
				j -= w[i-1]; //w[i-1]
			}
			i--; // 已经找到一个商品了，找下一个商品
		}
	}
}