一、导语
二、树及二叉树
1.树结构图示
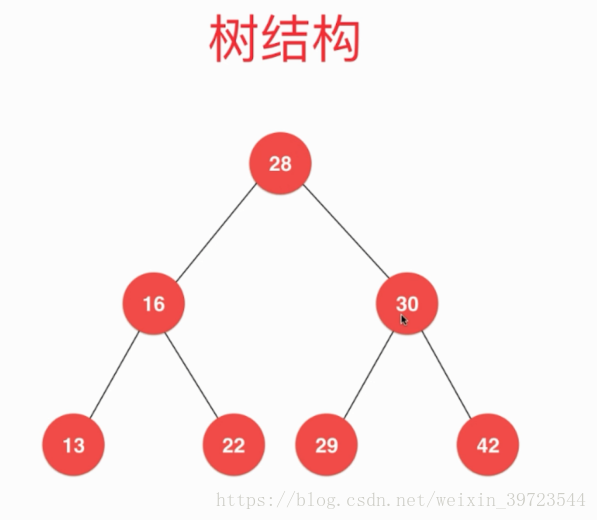
2.树的一些基本概念
1、结点:树中的数据元素都称之为结点
2、根:最上面的结点称之为根,一颗树只有一个根且由根发展而来,从另外一个角度来说,每个结点都可以认为是其子树的根
3、父亲:结点的上层结点
4、兄弟:具有相同父亲的结点称为兄弟
5、结点的度:结点所拥有的子树的个数称之为结点的度
6、树叶:度为0的结点,也叫作终端结点
7、分支结点:度不为0的结点,也叫作非终端结点或内部结点
8、结点的层次:从根节点到树中某结点所经路径上的分支树称为该结点的层次,根节点的层次规定为1,其余结点的层次等于其父亲结点的层次+1
9、树的深度:树中结点的最大层次数
3.二叉树
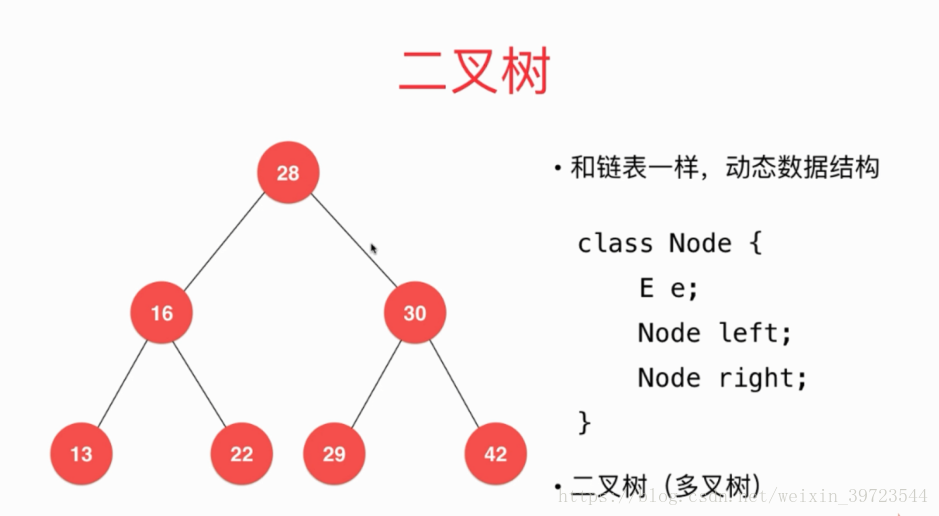
概念:其每一个结点都不能多余两个子节点。
二叉树的一个性质是一颗平均二叉树的深度要比及结点个数小得多,这个性质很重要,尤其对于特殊类型的二叉树即二叉查找树而言,其深度的平均值是O(logN),这将大大降低查找时的时间复杂度。
当然,二叉树在运用得不好的情况下的情况下是有严重的问题的,即:
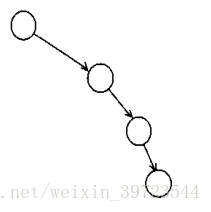
退化成一个类似于链表的结构。这种树被称为不平衡的二叉树,当然也有平衡的二叉树:如后面要介绍的AVL、红黑树等。
三、二分搜索树
需要以下 条件:
- 二分搜索树是二叉树
- 二分搜索树每个结点的值:大于其左子树的所有结点的值;小于其右子树的所有结点的值
- 其每一个子树也是也是一个二分搜索树。
如下 :
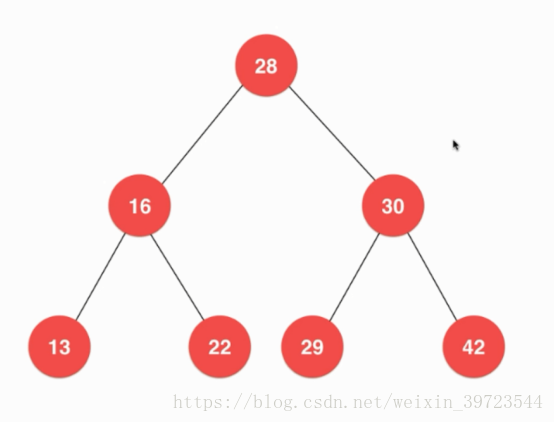
得出二分搜索树的性质: - 存储的节点的必须有可比较性。
四、其他(后续补充)
- AVL树(后续补充)
- 红黑树(后续补充)
参考:http://www.cnblogs.com/xrq730/p/5187032.html
《算法导论》相关内容








 本文深入探讨了树和二叉树的基本概念,包括结点、根、父结点、兄弟结点、结点的度、树叶、分支结点、结点的层次和树的深度。特别关注二叉树的特性及其在二分搜索树中的应用,讨论了二分搜索树的性质和条件,以及其在数据存储和检索中的优势。
本文深入探讨了树和二叉树的基本概念,包括结点、根、父结点、兄弟结点、结点的度、树叶、分支结点、结点的层次和树的深度。特别关注二叉树的特性及其在二分搜索树中的应用,讨论了二分搜索树的性质和条件,以及其在数据存储和检索中的优势。
















 1041
1041

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








