无人驾驶车辆模型预测控制配套代码_代码解析之自行车模型在Apollo规划中的应用...

在进行无人车的轨迹规划时，需要考虑无人车的车辆模型，才可以规划出符合车辆运动特性的、舒适的、容易被跟踪的路径。常用的车辆运动学模型有自行车模型和阿克曼转向几何模型，自行车模型实际上是对阿克曼转向几何的一个简化。

我在之前分析Apollo Hybrid A* 算法时，提到了它使用自行车模型，在当前状态的基础上，计算下一步可行驶的状态，即 Baidu Apollo代码解析之Open Space Planner中的Hybrid A* 这篇博客中的下列代码。对于车辆状态（x, y, phi），x和y的推算很简单，这里讲一下phi的推算的依据。

silver bullet：Baidu Apollo代码解析之Open Space Planner中的Hybrid A*​zhuanlan.zhihu.com

//扩展节点，扩展一个node就是扩展了一个grid，但是会产生多个在同一grid内的路径点

本文主要参考了 Apollo代码学习(二)—车辆运动学模型 和 无人驾驶汽车系统入门（五）——运动学自行车模型和动力学自行车模型 2篇博客。同时，推荐一篇论文《基于多传感器多路径规划自动泊车系统仿真及实车验证》便于理解。

Apollo代码学习(二)-车辆运动学模型_人工智能_follow轻尘的博客-优快云博客​blog.youkuaiyun.com

无人驾驶汽车系统入门（五）--运动学自行车模型和动力学自行车模型_Python_AdamShan的博客-优快云博客​blog.youkuaiyun.com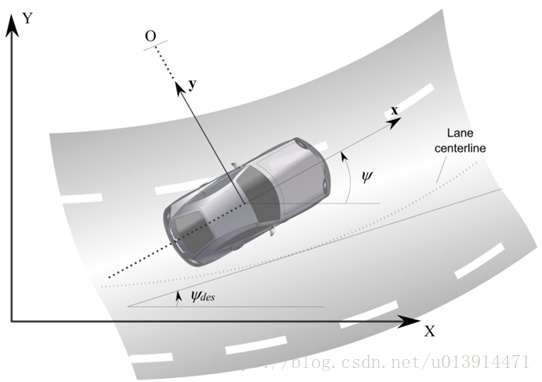

1. 代码中的steering是什么含义？

steering的计算思路我在代码注释中分析过了，steering由max_steer_angle_ 推算而来，因此首先要理解max_steer_angle_ 是什么。max_steer_angle_ 在HybridAStar类的构造函数中初始化。

在自行车模型中，假设后轮朝向与车体朝向始终相同，因此，相对于车体的后轮转角恒等于0，由前轮控制、影响车辆的朝向，也就是说，转动方向盘导致的方向盘转角（即通常意义上的steer）变化，都反映到前轮转角（相对于车体）的变化上了，再由前轮转角影响到车体朝向（phi）。那么，方向盘转角和前轮转角的量化关系是怎样的呢？在Apollo中，假设了该量化关系是线性的（或许是在某种条件下的近似），即前轮转角 = 方向盘转角 / 某个比例。对应max_steer_angle_ 的赋值代码来看，vehicle_param_.max_steer_angle() 就是车辆允许的最大方向盘转角，vehicle_param_.steer_ratio() 就是线性关系的比例参数，而max_steer_angle_ 就是车辆允许的最大前轮转角。综上，steering是车辆的前轮转角大小。

HybridAStar

2. 为什么下一个状态的车体朝向这样计算？

抛开NormalizeAngle()不谈，代码中 新的朝向 = 旧的朝向 + 行驶距离 / 轴距 * tan(前轮转角)。这个式子的依据是什么呢？

const 

假设短时间内，车辆的角速度是恒定的，则

。而角速度

。则

行驶距离 / 转弯半径。

如图1，以后轴中心为参考基准，在直角三角形 O-前轮-后轮 中，

。那么

，

next_phi = last_phi + 行驶距离 / 轴距 * tan(前轮转角)，得证。

图1 以后轴中心为基准的自行车模型

3. 参考文章2中的车体朝向计算方式与此不同，怎么理解？

文章 无人驾驶汽车系统入门（五）——运动学自行车模型和动力学自行车模型 中，以车辆质心为参考基准，如图2所示。其（x, y, phi）的更新方式如图3所示。

图2 以车体质心为基准的自行车模型

图3 参考文章2中的状态计算

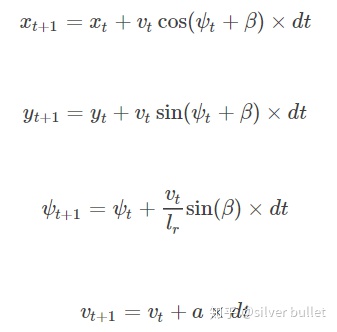
此时，

和

w * dt = v * dt / R = 行驶距离 / 转弯半径 依然成立。不同之处在于如何求R。在图2左侧直角三角形 O-后轮-质心 中，

。那么

next_phi = last_phi + v * dt * sin(β) / Lr = last_phi + 行驶距离 / Lr * sin(β)。

4. 2种不同的计算方式的区别有多大？

对比2个式子，不同之处在于 行驶距离 / 轴距 * tan(前轮转角) 与 行驶距离 / Lr * sin(β)。对比图1和图2，当 L << R 时，前轮转角与β都会很小，tan(前轮转角) ≈ 前轮转角，sin(β) ≈ β，且 前轮转角 ≈ 2*β， 轴距 ≈ 2*Lr。二者几乎相等。

5. 题外话——向心加速度

Apollo在 Lattice Planner 中会对采样构造的横纵向轨迹进行评估，其中一项是计算向心加速度，代码如下。其实向心加速度就是车辆的横向加速度。那么

假设车辆偏离参考线较小，即

较小，则

。那么

因为车辆偏离参考线较小，代码中使用参考线映射点的曲率来近似自车所在位置的曲率，即 ref_point.kappa()。

double