卷积计算公式_深度学习中卷积计算(coarse)指南

• 前言

卷积的计算是CNN中最基本的算术单元，卷积的计算过程中出现的：Input Feature Map(FP), Output Feature Map(FP), 以及与 Kernel(size, strides, padding， dilation rate等)之间的关系和计算方式是我们应该掌握的基本知识。笔者在这里对其进行简要介绍。

• 卷积Input FP size 与 Output FP size之间的计算公式

1、如图1所示， 其展示了从Input FP 经过卷积计算得到 Output FP的过程，每个通道相互之间独立；

                                             图 1：卷积计算示意图

2、假设Input FP的channels数为n_in， Output FP的channels数为n_out为例，kernel为方形，大小为k, Input FP的Padding为p, 卷积计算的步长(stride)为s。则输入输出的关系如下：

3、如图2计算示意图；由于卷积计算采用权值共享，输出的FP的每个channel是由输入FP经过n_in个卷积后采用elementwise add叠加得到一个Output FP channel，一个channel卷积的参数量为n_in * k * k，Output FP channel有n_out个channel, 所以整个卷积核参数量为：n_in * k * k * n_out.

                                     

        图 2：Input FP(Channel: 2), Output FP(Channel: 3), Kerenl(Size: 3x3)

• 卷积计算方法(Convolution as a matrix operation)

以3*3卷积核K对4*4的特征图(FP)I做计算为例，将输入FP按从左到右，从上往下展开成一个16-d的向量I_vector，那么对应的3*3的卷积核应该展开如下C(4 * 16)：

然后C * I_vector ==> O_vector(1*4); 最后对O_vector处理成2*2，得到输出FP。

• 感受野计算(Receptive Field Arithmetic)

两层之间的感受野是指下层的FP中某一点对应上一层的size， 也就是kernel的大小。但是这里要讨论的是，某一层FP中像素对应与原始输入图像的感受野(RF)的大小如何计算？

这里笔者先直接给出计算公式，然后解释下公式中参数的定义，同时读者自己需要手推揣摩这种计算方式。

                                  

1、公式第一行中的参数定义与上述一样；

2、第二行中的j_in表示当前层的Jump, 这个参数与stride相关，其表示截至到目前层的总stride，该j直接影响第三行中r的计算；

3、第三行中r表示当前层FP中的某一个点对应的感受野的大小。

• 空洞卷积(Dilated Conv)输入与输出尺寸计算公式

dilate_rate为d， kernel的尺寸为k的卷积核的有效尺寸为：K = k + (k-1)*(d-1)

则有：输出o与输入i尺寸之间计算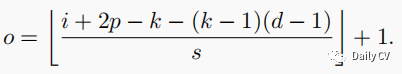                                        

参考：

1、A guide to convolution arithmetic for deep learning.

2、A guide to receptive field arithmetic for Convolutional Neural Networks.