什么是KMP?
kmp是一种字符匹配算法,可以用来比较一串字符(父串S)中是否包含另一串字符(子串P)。
接下来讲一下大体思路,后面细说。
比起暴力匹配,kmp借助子串自有的信息来规避必定错误的匹配,实现优化。

那kmp是怎么做到匹配错误时,避免从头开始,而是直接跳到x位置呢?
你会发现,在“起跳”位置D,与“落地”位置C,前面都有个AB。
而ABC属于子串P的一个前缀[1],ABD属于子串P的一个后缀。这两个缀不同的地方在最后一个字母D和C。
当D与父串S不匹配时,就会跳到和它相同前缀的ABC,让C与父串S比较。也正是因为他们有相同的前缀,跳转才不会失败。
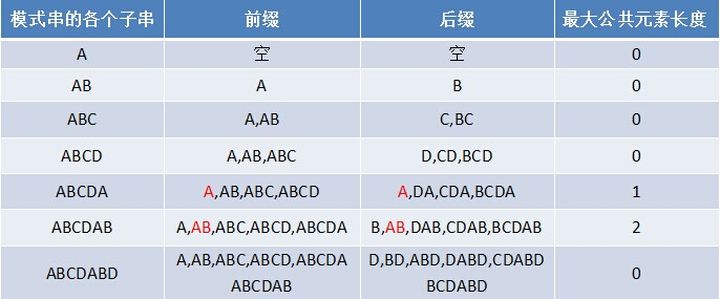
例如“ABCDABD”的“最长公共前后缀表”为:
而D是最后一个值2,当字符不匹配时就跳转到2(第三个位置)重新匹配
什么是最长公共前后缀?
若是给你一个字符串,你会用什么方法得到这个字符串的最长公共前后缀呢?
你会很自然的把它复制两份,从头开始一一对比,就像子串与父串比较那样
例如“ABCDABD”:
- 将A与B比较,发现不同
- C,D同理,直到再次匹配到A(下标4),
- 拿起B(下标1)与匹配到的第二个位置(下标5)比较,发现B与B相同,
- 拿起C(下标2)与匹配到的第三个位置(下标6)比较,发现C和D不同,放弃匹配。
- 将A与剩下的BD比较,发现都不同
但是这个方法比较慢,慢在最后一步“将A与剩下的BD比较”
突破口在刚刚那张图里的“各个子串”。
从“A”到“AB”是怎么计算公共前后缀的?或者换个问法
若是你知道了“ABCDAB”的最长公共后缀,你可以知道“ABCDABD”的吗?
具体操作如下:
- 两个指针(k,j)放在字符数组
上
- 创建一个next数组,用来存放以为结尾的字符串有多长公共前后缀。
- 令
只有三步:
- k=-1时,同时移动,
- 字符相等,同时移动,
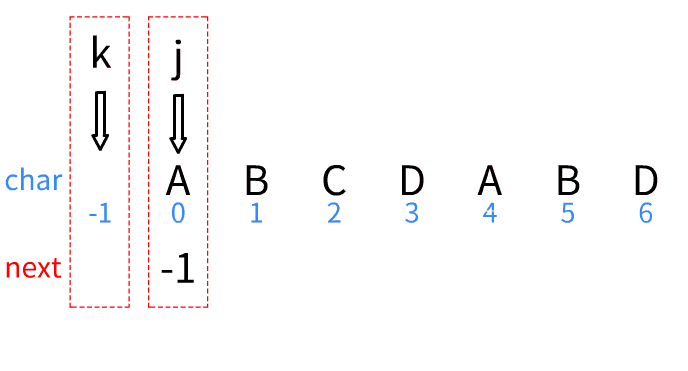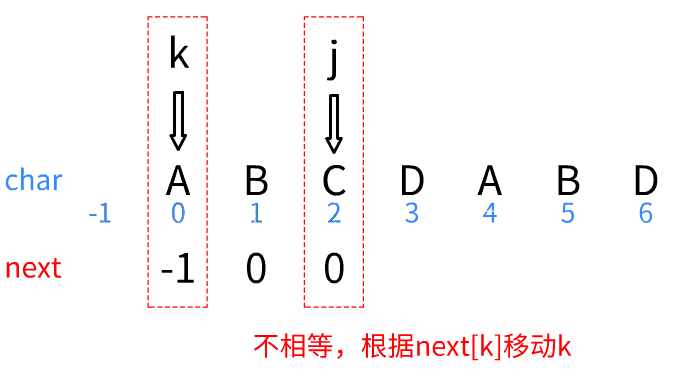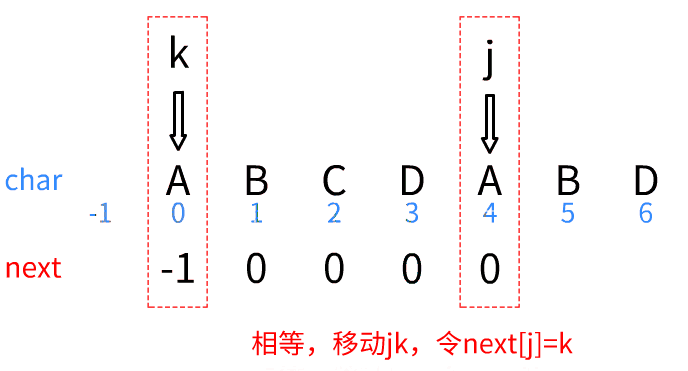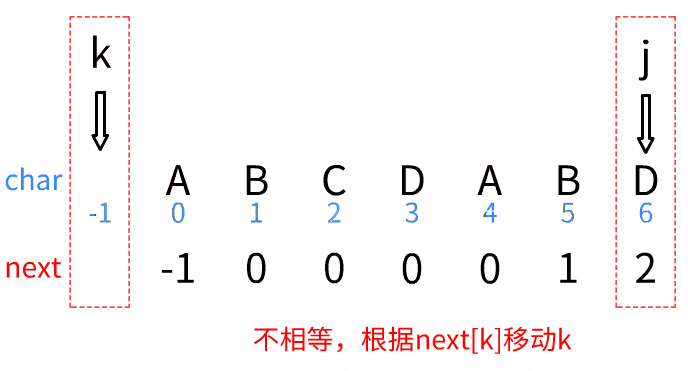
- 字符不相等时,根据移动k
一点一点解释:
对于字符串“ABCDABD”,用来存放以j为结尾的字符串有多长公共前后缀的数组应该为
- 全部往右移动一格:
(1)计算出的next数组是需要当作“参考跳转表”的。若是不移动,当位置匹配到D而不适配时,就需要从前一个位置B那里,才能拿到“相同前缀”的地方。
(2)与其说是右移动,不如说是用“-1”的代价,导致后续匹配时被“强行-1”。而这个“代价”刚好成为了(1)的优势 - 将next[0]设为-1:前缀的第一个值设为-1,这样在比较时才可以清楚的知道“当前匹配的字符为第一个”。若是“连第一个都匹配不上”,则会对k进行“暂时的流放”,等待j移动到下一个位置,k又会重新回归,对新的字符进行比较。而这个过程与第二步“字符相等”时操作一样,所以可以把步骤1,2合并起来。
回到刚刚说的“突破口”
为什么k能够利用
因为k用的都是“j曾经走过的路”,是之前“慢慢累积起来”的数据。从一个字符到两个,从两个到三个,j利用k不断拓宽边界,k也在利用“j的遗产”来指导j。而“最后跳两下”也是k在尽力帮j,在满足前缀相同的条件下获得更大的数字,而跳到-1时,就相当于k在对j说:“兄弟,你以前留下的东西只允许我帮你到这了,删档玩下个号吧”。
回到最开始,
继续回到kmp
现在你一手拿着子串P,一手拿着next数组,准备开始干父串S,但是心中还有疑问:为什么我拿着一个“最长前后缀表”就可以跳的不出错了?为什么是子串的后缀跳前缀,如果有相同的“中缀”,不能跳到“中缀”吗?
第一个问题:在跳之前,是不是得要先“匹配出错”,那出错之前呢?出错之前是不是已经有些字符匹配了,才能轮到这个字符“不匹配”?而在那些“已匹配”的字符中,本身就包含着子串P的字符。所以根据“匹配出错”的前一个位置的后缀,跳转到相同的前缀就不会出错。
第二个问题:举个例子:“ABABCABD”,为什么后缀ABD只能跳到前缀ABA,而不是中缀ABC?
因为最终是要和父串S比的,若是你能保证后缀与前缀相同,那么跳过去不会错;但若是你跳到中缀,就相当于拿着“前缀+中缀”去比较后缀。如果例子是“ABABAB”,那确实可以从“后缀AB(4,5)”跳到“中缀AB(2,3)”,那是因为中缀AB本身就包含在了“前缀ABAB”和后缀“ABAB”里了。
kmp的具体流程其实和填充next数组相似:
创建两个指针
这个过程是不是很熟悉呢,
若是想参考具体代码,可前往leetcode28.实现strStr()的题解区
顾不问:算法入门笔记-目录zhuanlan.zhihu.com参考
- ^前缀是从头往后数,后缀是从后往前数,但是相互比较时,比较顺序是一个方向。
























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








