c++分治法求最大最小值实现_最优化计算与matlab实现（14）——非线性最小二乘优化问题——L-M法...

参考资料

《精通MATLAB最优化计算（第二版）》

编程工具

Matlab 2019a

目录

石中居士：最优化计算与Matlab实现——目录​zhuanlan.zhihu.com

---

L-M法（Levenberg-Marquardt法）

• 原理

当矩阵

为病态矩阵时，用G-N算法可能得不到正确的解，甚至当

不可逆时，这时G-N算法就无法计算下去。L-M算法通过采用系数矩阵阻尼的方法改造矩阵

的性态，使算法能够进行下去。

L-M算法中有两个主要的步骤：一是解方程

（其中

为阻尼系数）求出自变量的增量，另一个是阻尼系数

的调整算法。

• 算法步骤

用L-M法求解非线性最小二乘优化问题

的算法过程如下：

【1】给定初始点

，选取参数

，

及精度

，置

；

【2】计算

；

【3】计算

；

【4】计算

；

【5】令

解方程

；

【6】令

，计算终止条件是否满足，不满足转【7】；

【7】若

，令

，转【8】，否则令

，转【5】；

【8】令

，转【2】。

• Matlab代码与试算

用L-M法求下面的优化问题：

，其中初始点取

，参数

。

test.m

syms 

Levenberg_Marquardt_Method.m

function

命令行窗口

x_optimization =

    1.0410


f_optimization =

    1.9582

图像

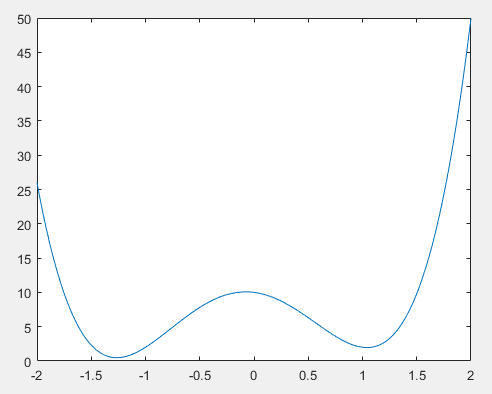
初始点为5时，求出的是极小值，而不是最小值。初始点为-5时，能求得最小值。

---

---

目录

石中居士：最优化计算与Matlab实现——目录​zhuanlan.zhihu.com

---