皮尔逊相关系数_皮尔逊相关系数（Pearson Correlation Coefficient）

    散点图检验显示，两个连续变量的散点呈直线趋势，则认为二者存在直线相关趋势(简单相关趋势)。皮尔逊相关系数(Pearson Correlation Coefficient)，也称乘积相关系数，是一种线性相关系数，用来反映两个符合正太分布的连续变量线性相关程度的统计量；用r来表示样本相关系数、ρ(读音接近rao)表示总体相关系数，r是ρ的估计值。两个变量来自同一个个体，可以是：

eg1. 身高  、  体重

eg2. 年龄  、  工作家庭增益     

eg3. 办公护士久坐工作时间 、  胆固醇浓度

eg4. 急诊护士心理弹性量表得分  、  情绪劳动量表得分

eg5. 环绕立体四面八方声音的累积分贝  、  每周平均入睡时间

        Pearson相关系数的适用条件：①适用于线性相关的情形，对于曲线相关等更为复杂的情形、积差相关系数的大小并不能代表相关性的强弱。②无明显异常值，存在极端值则予剔除或转换。③变量呈双变量正态分布，如各自服从正态分布两个变量计算Pearson相关系数、假阳率偏高一点。

      利用样本相关系数推断总体中两个变量是否相关，可以用t 统计量对H0假设(即二者相关系数为0)进行检验。若t检验显著，则拒绝原假设，即两个变量是线性相关的；反之，则不能拒绝原假设，即两个变量不是线性相关的。

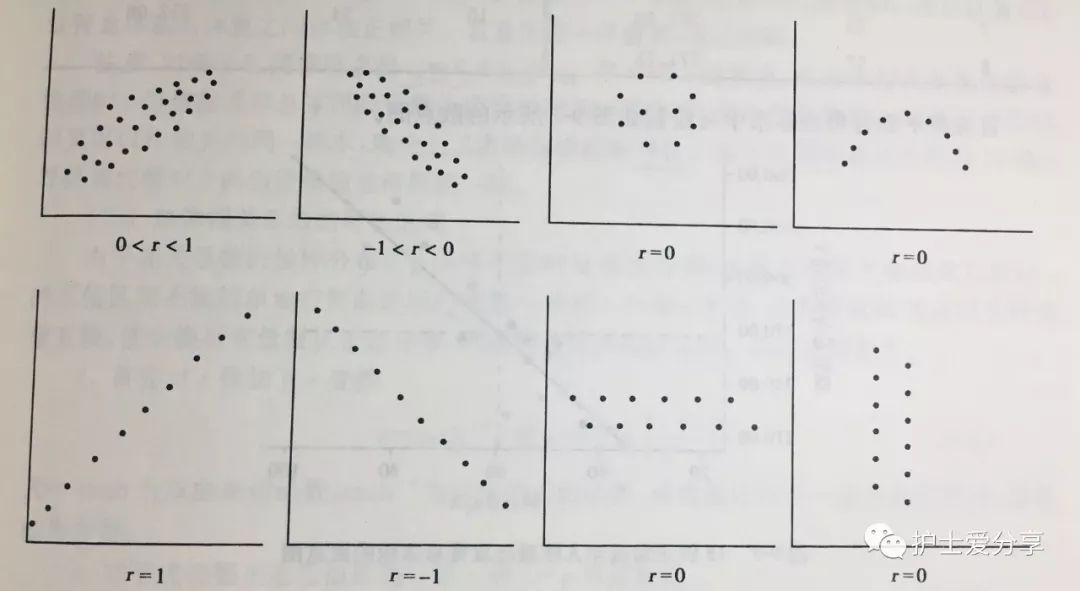
图9-6 直线相关示意图(医学统计学第3版)

     r的取值为，-1~+1。r＞0表明两个变量是正相关，即一个变量的值越大，另一个变量的值也会越大；r＜0表明两个变量是负相关，即一个变量的值越大另一个变量的值反而会越小。r 的绝对值越大，则两变量相关性越强。若r=0，表明两个变量间不是线性相关，但可能存在其他方式的相关(比如曲线方式)。

(1)一般认为：|r|≥0.8时，可认为两变量间高度相关；0.5≤|r|<0.8，可认为两变量中度相关；0.3≤|r|<0.5，可认为两变量低度相关；|r|<0.3，可认为两变量基本不相关。

(2)也有认为：|r|≥0.8时，可认为两变量间极高度相关；0.6≤|r|<0.8，可认为两变量高度相关；0.4≤|r|<0.6，可认为两变量中度相关；0.2≤|r|<0.4，可认为两变量低度相关；|r|<0.2，可认为两变量基本不相关。

(3)还有认为：|r|≥0.7时，可认为两变量间强相关；0.4≤|r|<0.7，可认为两变量中度相关；0.2≤|r|<0.4，可认为两变量弱相关；|r|<0.2，可认为两变量极弱相关或不相关。

        不论如何，图中论文有明显的错误：r =-0.198(P＜0.01)并不相关。

注：

(1)相关关系≠因果关系。

eg1. 一个人家里打火机的数量  、 这个人得肺癌的几率

eg2. 本季度冰淇淋的销量 、 泳池里淹死的人数

(2)相关系数r并不成比例关系。

eg. 相关系数0.6大于0.2≠前者是后者的3倍，因为r=0.6、r²=0.36是指两变量共享36%的方差。