拉格朗日乘数法_条件极值与拉格朗日乘数法

对于条件极值问题，当条件形式较为简单时可以采用消元法，将多元函数求条件极值问题转化为单变量函数的极值问题。但当问题的维数增加以及限制条件变得更加复杂的时候，消元法往往难以求解。下面介绍一个求条件极值问题的常用方法——拉格朗日乘数法。

考虑模型：二元函数在平面曲线上的极值

求二元函数

的极值，其中

受条件

限制，即

在讲解之前先明确几个《高等数学》中的概念

1. 对于二元函数
   ，其
   梯度为其两个偏导数组成的向量
   ；梯度的方向代表
   函数值增长最快的方向，相应的梯度的反向对应函数值下降最快的方向；梯度的模对应增长率。
2. 对于平面曲线
   ，其对应于曲面
   被平面
   所截的曲线；在曲线上的梯度
   对应于曲线的
   法向量；曲线的方向向量与法向量垂直，为
   。

为方便理解，下面的讲解希望尽量通过几何意义来使得公式的导出更加形象化，为此不得不放弃一些严谨性。

用符号

和

分别表示梯度向量和方向向量

条件极值图示

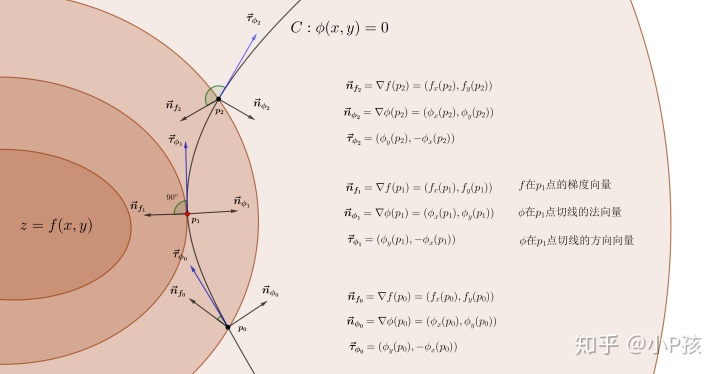
如上图所示，当点沿着曲线

移动的时候，如果在某点

切线方向向量

和梯度向量

的夹角

• 时(
  点)，点沿着
  的方向移动，
  的值会增大；
• 时(
  点)，点沿着
  的方向移动，
  的值会减小；
• 时(
  点)，此时该点对应函数
  在
  上的一个条件极值点。

可以看出取极值的必要条件是

的梯度向量与

的方向向量垂直，或者说

的梯度向量与

的法向量共线。基于这样一个想法，给出下面的方程组

其中，第一个等式的意义是

的梯度向量与

的法向量共线；第二个等式是曲线

本身的约束。由上面所讨论的条件极值的几何意义，可知

式这个方程组的解就对应于

在

上的条件极值点。

当问题由二维变成三维的时候，

式将对应为

此时上面的第一个式子对应着两个约束等式，为方便求解这个方程组，我们引入一个辅助变量

，称其为

拉格朗日乘数，令

于是

式可以改写成

式为拉格朗日乘数法的一般表示形式。

此外我们引入拉格朗日函数的概念

进一步将

式转化为

[例1] 用拉格朗日乘数法求解下面条件极值问题

由拉格朗日乘数法将原条件极值问题转化成方程组的求解，写出拉格朗日函数

对应的方程组为

求解方程组

得到

于是函数

在点

处取得极值，进一步判断函数在该点取

极小值，极值为

。

更一般的情况，对于n元函数和m个等式约束的条件极值问题，拉格朗日函数如下

可将问题转化为求解一个有

个变量

个等式的方程组

该方程组的解对应原条件极值问题的极值点。

以上讨论的范围都是限制条件为等式的情况，而在机器学习领域中的模型往往都是带不等式约束的，不等式约束条件极值问题的拉格朗日乘数法将在下次更新中讨论。

最后，第一次在知乎写文章，不当之处请多指正｡◕‿◕｡