标准正态分布_Student‘s t分布和标准正态分布

在统计分析的假设检验中，在总体方差未知时，常用的U统计量表示的不能用来构造的置信区间，因为此时它还含有位置参数。一个自然的想法是用样本标准差S去估计总体标准差，此时

就不再服从标准正态分布N(0,1)，而涉及t分布。

如果，且X与Y独立，则

的分布称为自由度为n的t分布，记为t(n)。

t分布是统计中常用的概率分布之一，它仅含一个位置参数n，这个参数称为自由度。自由度为的分布的密度函数有如下形式

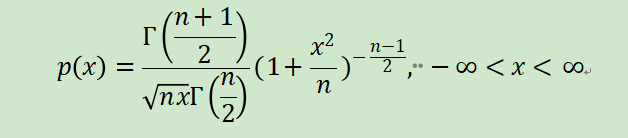
t(n)的密度函数是偶函数，它是关于纵轴对称的单峰函数，形状与标准正态分布相似，但峰比的N(0,1)峰低一些，两侧尾部厚一些，这表明t分布的取值的分散程度要比N(0,1)大一些。

可以从下图中看到，在x轴2-4范围与分布线包含的面积上，标准正态分布要比t分布包含的面积小的多，通过微积分我们可以准确测算出这部分面积的数值(就是指取值落入2，4这一范围的概率)，从而可以认为在2-4的范围内，t分布出现数值落入的概率(也就是出现极大值的概率)比标准正态分布要大，故这种现象被我们称为肥尾现象(fat tail or heavy tail)

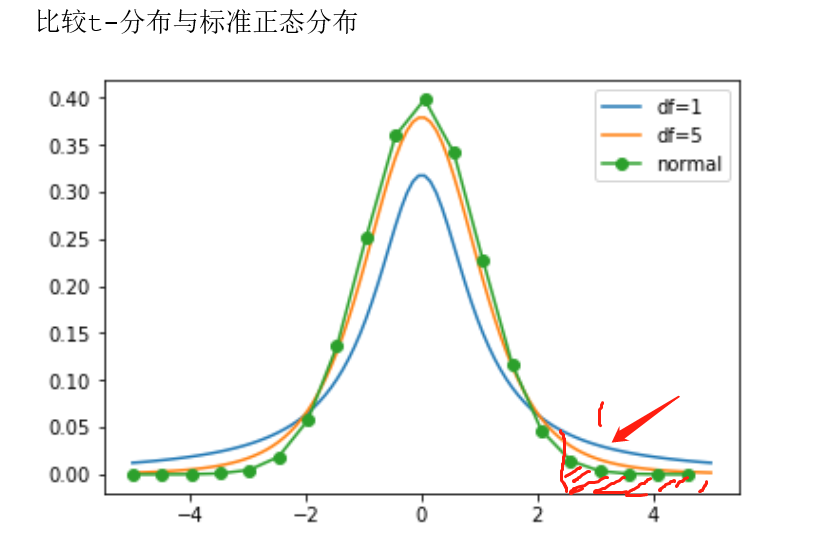
其实t分布这一肥尾现象的产生就是受到自由度n这个参数的影响，(the degrees of freedom has the most important effect on the shape of the tails)

Kurtosis[t(n)]=3*(n-2)/(n-4)

从上面的公式不难看出，t分布的峰度仅仅受到自由度n这一参数的影响，事实上，t分布在实践中非常适合对许多资产的收益率做拟合，它更容易抓住资产收益率的肥尾特征(意味着一个资产出现极端收益率的概率相对较大)。

但由于随着自由度n的增大，t分布与N(0,1)之间的差别就越来越小，比如，从下图可见，自由度为10的t分布已很接近标准正态分布了。所以

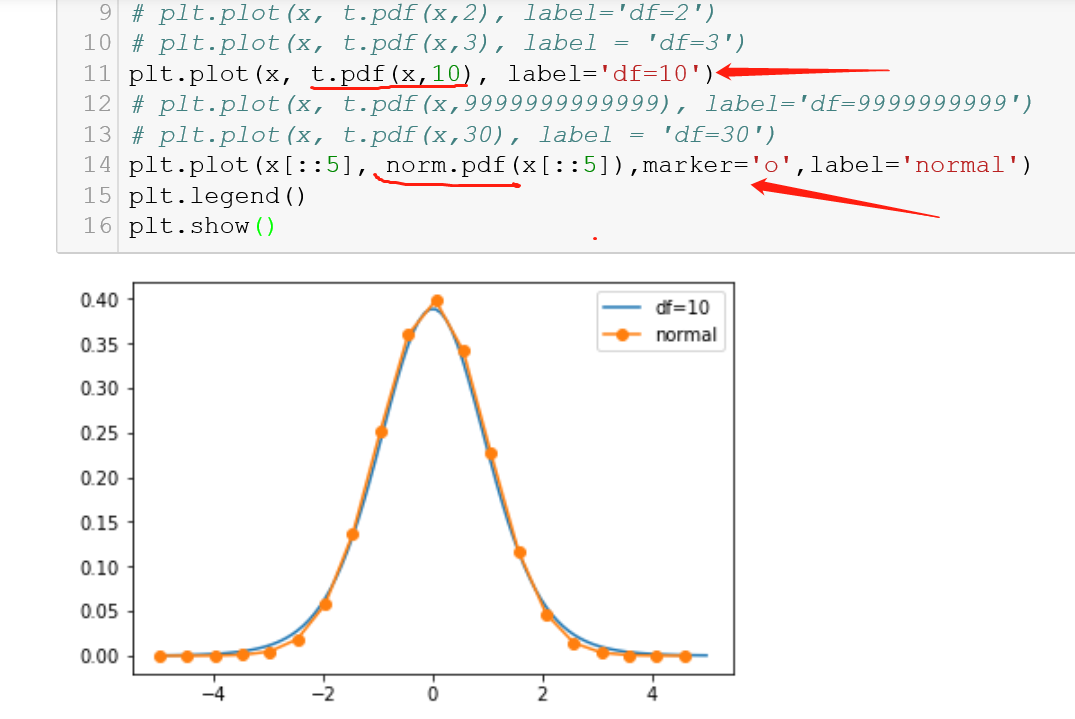
在n=25时已经基本就是正态分布，加上中心极限定理(CLT)的加持，n越大，t分布就像一个正态分布。所以延伸开来，对于VaR(Value at Risk)的估计，本来用t分布的效果就应该比正态分布要好，但是由于样本肯定是大样本的缘故，所以最终对VaR的估计方面仍然使用了正态分布法(analytical method)。

而自由度为1的分布的密度函数

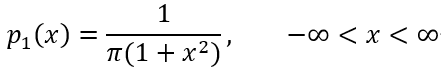
这便是柯西分布，其特点数学期望与方差均不存在。

干货总结(附英文)

关于t分布在CFA和FRM考试中的常用总结：

1 t分布更容易捕捉厚尾现象，是一个比标准正态分布更 fat tail的分布

it captures the heavy or fat tails in asset return(i.e. ,the increased likelihood of observing a value larger than relative to a normal distribution).

2 更适合拟合资产的收益率

t distribution makes it better suited to modeling the returns of many assts than normal distribution.

3 标准正态分布是t分布的极限分布

A standard normal distribution is the limiting distribution as n

goes to infinite.

4 t分布更尖峰，更肥尾，在+or-1.5的x轴范围内有着更小的概率取值。

The Students's t is more peaked, heavier-tailed, and has less probability in the region around +or-1.5.

5 t分布在假设检验中更适用与小样本(n<=30)

The Students's t distribution was originally developed for testing hypotheses using small samples.