Python中使用EMD（经验模态分解）

在Python中使用EMD（经验模态分解）进行信号分解时，通常可以设置信号分解的数目。EMD算法的目标是将信号分解成多个称为“本征模态函数”（Intrinsic Mode Functions，简称IMF）的成分，每个IMF都代表了信号中的不同频率成分。你可以通过控制分解过程中的停止条件来控制生成的IMF的数量。

一种常见的停止条件是确保生成的IMF满足一些特定的性质，如以下之一：

能量或方差的百分比：你可以设置一个阈值，当生成的IMF的能量或方差低于该阈值时停止分解。这可以帮助你控制IMF的数量。

IMF数目：你可以设定要分解的IMF的最大数量，当达到这个数量时停止分解。

残差的能量：分解过程会生成一个残差信号，可以计算其能量。你可以设置一个阈值，当残差的能量低于该阈值时停止分解。

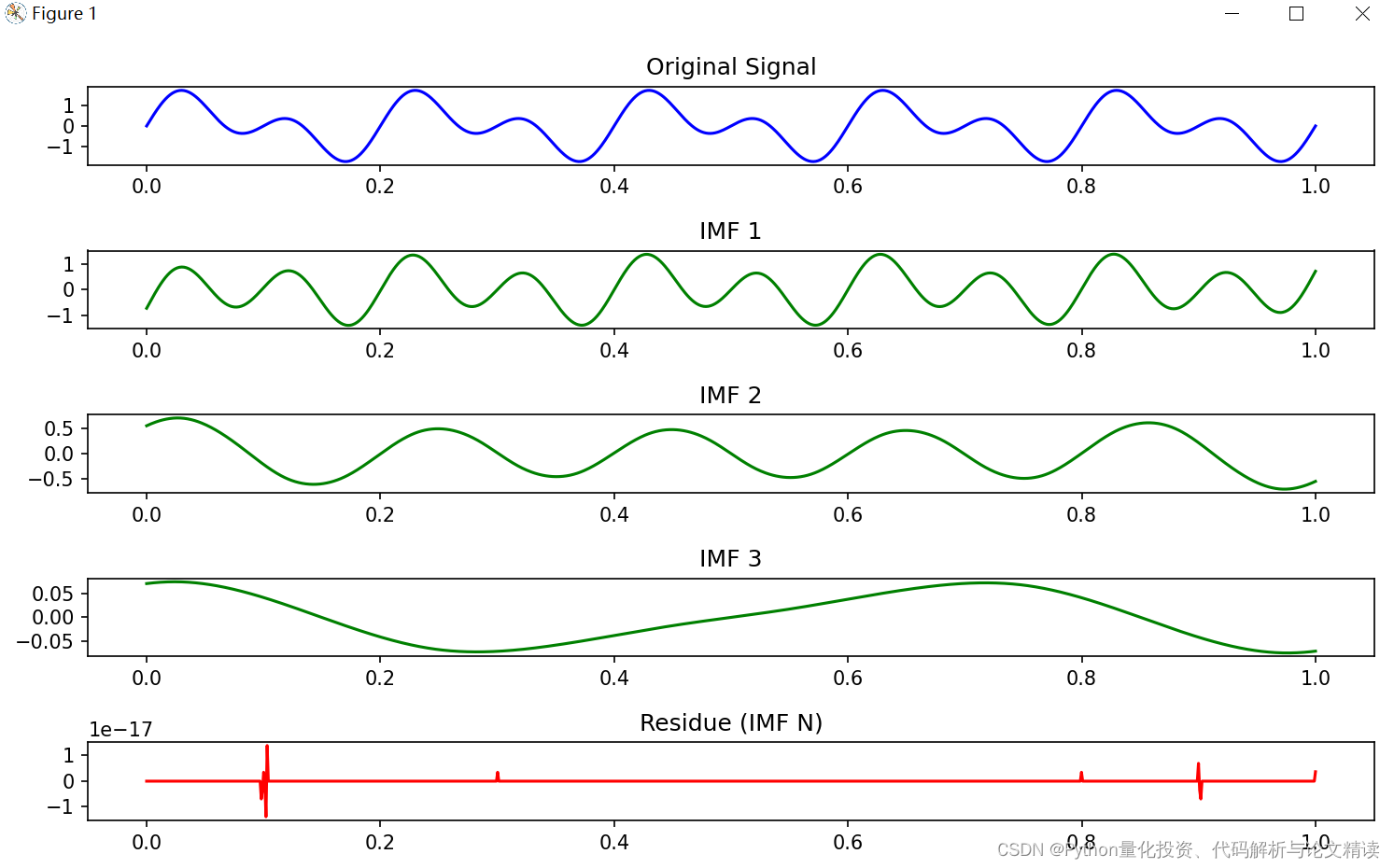
以下是一个使用PyEMD库进行EMD分解并设置IMF数量的简单示例：

from PyEMD import EMD
import matplotlib.pyplot as plt

# 创建一个示例信号
t = np.linspace(0, 1, 1000)
signal = np.sin(2 * np.pi * 5 * t) + np.sin(2 * np.pi * 10 * t)

# 创建EMD对象
emd = EMD()

# 设置分解的IMF数量
num_imfs = 3

# 执行EMD分解
imfs = emd(signal, max_imf=num_imfs)

# 计算残差项
residue = signal - np.sum(imfs, axis=0)

# 可视化展示
plt.figure(figsize=(10, 6))

# 原始信号
plt.subplot(num_imfs + 2, 1, 1)
plt.plot(t, signal, 'b')
plt.title('Original Signal')

# 绘制各个IMF
for i in range(num_imfs):
    plt.subplot(num_imfs + 2, 1, i + 2)
    plt.plot(t, imfs[i], 'g')
    plt.title(f'IMF {i + 1}')

# 绘制残差
plt.subplot(num_imfs + 2, 1, num_imfs + 2)
plt.plot(t, residue, 'r')
plt.title('Residue (IMF N)')

plt.tight_layout()
plt.show()