一、基本概念
1、先验概率:
定义:由以往数据分析得到的概率
根据大量样本情况的统计,在整个特征空间中,任取一个特征向量x,它属于类Wj的概率,即P(wj)。
如果总共有c个类别
P(w1)+P(w2)+...+P(wc)=1
2、后验概率
当我们获得了某个样本的特征向量X,则在x条件下样本属于类wj的概率P(wj|x)成为后验概率。
3、类条件概率
P(x|wj)是指当已知类别为wj的条件下,看到样本x出现的概率。
4、获取后验概率
通过贝叶斯公式
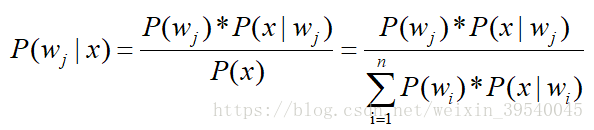
P(wj) 先验概率(总共有n个类别)
P(x|wj) 类条件概率
P(x) 由全概率公式求出的
二、最小风险贝叶斯分类
定义:最小错误率贝叶斯分类错误的概率最小,但是,每次分类错误带来的损失是不一样个的。
例如:要判断某人是正常(w1)还是肺病患者(w2),于是在判断中可能出现以下情况:
第一类:判对(正常—>正常) λ11;
第一类:判错(正常—>肺病) λ21;
第一类:判对(肺病—>肺病) λ22;
第一类:判错(肺病—>正常) λ12;
第二类和第四类属于分类错误
显然第四类错误带来的随时大于第二类错误带来的损失
为了评估分类错误的风险,引入以下概念:
- 决策αi: 表示把模式x判决为wi类的一次行动
- 判策空间:所有决策αi的集合
- 损失函数:λij = λ(αi, wj)
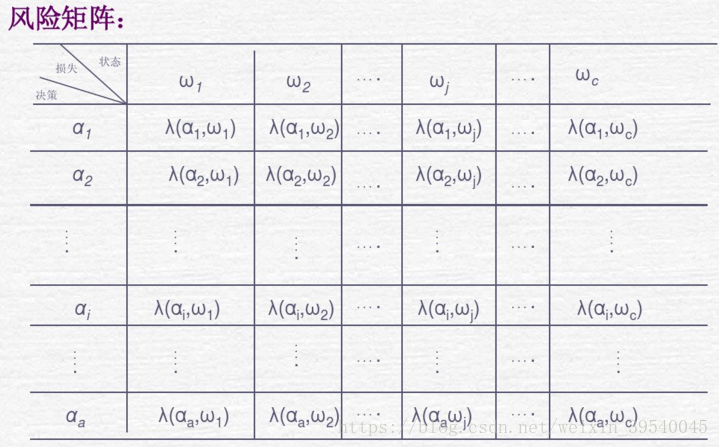
表示模式x本来属于wj类而采取的决策为αi时所带来的损失,这样就可以得到风险矩阵
- 条件风险(也叫条件期望损失):对于x采取一个判决行动αi(x)所冒的风险(或所付出的代价)
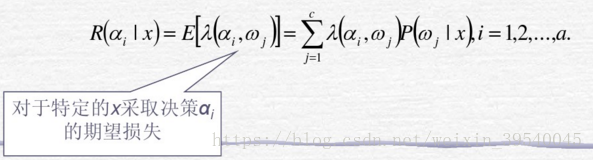
周立功《机器学习》

风险矩阵:
1、最小风险判决准则
首先举一个例子:






 本文介绍了贝叶斯分类的基本概念,包括先验概率、后验概率和类条件概率等,并详细阐述了如何通过贝叶斯公式计算后验概率。此外,还探讨了最小风险贝叶斯分类的应用场景。
本文介绍了贝叶斯分类的基本概念,包括先验概率、后验概率和类条件概率等,并详细阐述了如何通过贝叶斯公式计算后验概率。此外,还探讨了最小风险贝叶斯分类的应用场景。
















 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








