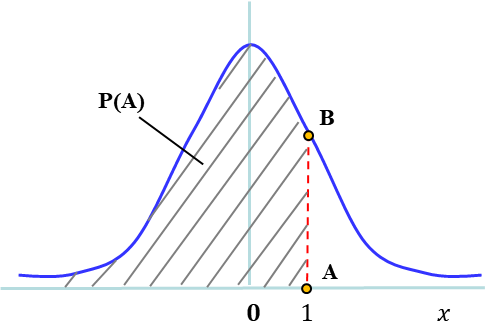
这里主要是指分位数、累积概率值与概率密度值的相互计算。三者之间的关系主要是曲线函数和概率函数。比如,知道分位数,要计算累积概率,或者计算概率密度值。如下图所示,斜线面积部分为
累积概率,累积范围为-∞到1,而该累积概率所对应的横轴位置1(A点)则称为其
分位数;而图中B点为曲线中的一点,对应横坐标为1,而纵坐标值又是多少呢?这里B点即是正态分布的
概率密度值。
 众所皆知,标准正态分布的平均值μ=0,标准差σ=1。在统计应用中,曲线之下与横轴的面积定义为1,那么,分位数为0时,累积概率就是0.5。对标准正态分布而言,概率值与分位数之间有标准表,只要知道分位数的大小,即可以查到概率值了。对于非标准的正态分布,在手工计算时,则需要进行标准化的转换。假如已知正态分布的均值和方差,要求分位数为X的概率函数,按以下转换公式将分位数X进行转换,将得到新的分位数
众所皆知,标准正态分布的平均值μ=0,标准差σ=1。在统计应用中,曲线之下与横轴的面积定义为1,那么,分位数为0时,累积概率就是0.5。对标准正态分布而言,概率值与分位数之间有标准表,只要知道分位数的大小,即可以查到概率值了。对于非标准的正态分布,在手工计算时,则需要进行标准化的转换。假如已知正态分布的均值和方差,要求分位数为X的概率函数,按以下转换公式将分位数X进行转换,将得到新的分位数
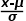 ,用新的分位数去查标准正态分布表即可。
,用新的分位数去查标准正态分布表即可。
 简单去理解,曲线下方的面积为1,但不同的正态分布形状是不一样
简单去理解,曲线下方的面积为1,但不同的正态分布形状是不一样
 众所皆知,标准正态分布的平均值μ=0,标准差σ=1。在统计应用中,曲线之下与横轴的面积定义为1,那么,分位数为0时,累积概率就是0.5。对标准正态分布而言,概率值与分位数之间有标准表,只要知道分位数的大小,即可以查到概率值了。对于非标准的正态分布,在手工计算时,则需要进行标准化的转换。假如已知正态分布的均值和方差,要求分位数为X的概率函数,按以下转换公式将分位数X进行转换,将得到新的分位数
众所皆知,标准正态分布的平均值μ=0,标准差σ=1。在统计应用中,曲线之下与横轴的面积定义为1,那么,分位数为0时,累积概率就是0.5。对标准正态分布而言,概率值与分位数之间有标准表,只要知道分位数的大小,即可以查到概率值了。对于非标准的正态分布,在手工计算时,则需要进行标准化的转换。假如已知正态分布的均值和方差,要求分位数为X的概率函数,按以下转换公式将分位数X进行转换,将得到新的分位数
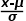 ,用新的分位数去查标准正态分布表即可。
,用新的分位数去查标准正态分布表即可。
 简单去理解,曲线下方的面积为1,但不同的正态分布形状是不一样
简单去理解,曲线下方的面积为1,但不同的正态分布形状是不一样







 这篇博客详细介绍了标准正态分布的概念,并探讨了如何使用标准正态分布表进行简单计算。对于统计学和数据分析爱好者,理解标准正态分布是至关重要的。通过实例解析,帮助读者更好地掌握这一关键工具。
这篇博客详细介绍了标准正态分布的概念,并探讨了如何使用标准正态分布表进行简单计算。对于统计学和数据分析爱好者,理解标准正态分布是至关重要的。通过实例解析,帮助读者更好地掌握这一关键工具。
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章
















 7457
7457

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








