多臂老虎机/多臂赌博机 （Multi-Armed Bandit）

多臂老虎机/多臂赌博机（Multi Armed Bandit）是强化学习（Reinforcement Learning）的一种特例——只有一个state

啥是MAB

如下图所示。casino里面有这样的一个机器，有多个摇臂（arm）可以去拉，每次要投币才能玩～～（就像抓娃娃机器那样哦）。 投币后可以选择其中一个摇臂拉一下（choose an action），然后有可能（有概率的）获得奖励（reward）。人品不好就两手空空了。

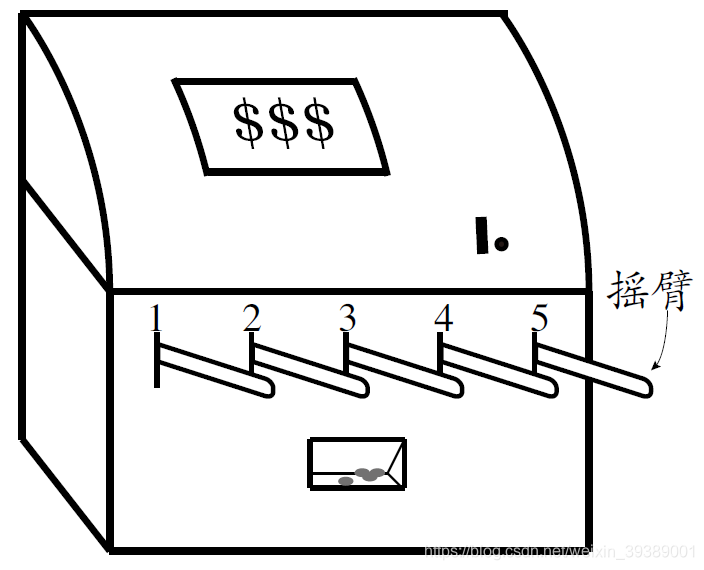
我们就是agent，和我们交互的环境（environment）就是这个老虎机。我们对环境的作用就是选择一个摇币拉动，叫做一个action。环境的反馈就是reward。
这就是一个强化学习的框架。只是环境状态是不会发生转移的，就是这个摇臂。一般来讲（简化这个问题），拉动每个摇臂能够获得的reward是一个随机数，这个随机数是服从一定的概率分布的，假设这个概率分布不会变。（但是我们不知道每个摇臂能吐出reward的概率，而且每个摇臂的概率是不同的）

总结一下：
**K-摇臂赌博机 (K-Armed Bandit)

• 只有一个状态，K个动作
• 每个摇臂的奖赏服从某个期望未知的分布
• 执行有限次动作
• 最大化累积奖赏**

困境是啥

我们不知道每个摇臂能吐出reward的概率是多少，因此我们要通过多次尝试来总结经验，估计每个摇臂的reward的期望（均值）。
理论上，如果我们足够有钱，把每个摇臂都拉动足够多的次数，那么就可以计算每个摇臂的reward的期望。然后再选择reward的期望最大的那个摇臂来拉，就可以了。
但是。。。怎么可能咧。。。妈妈只给了一点零花钱。。。
有限的次数中，又想探索哪个摇臂好，又想赶紧回本啊～要是谁已经探索完了，知道哪个摇臂的reward的期望最大，我就一直拉那个摇臂就好了（想的总是美）

**探索-利用窘境 (Exploration-Exploitation dilemma)

• 探索：估计不同摇臂的优劣 (奖赏期望的大小)
• 利用：选择当前最优的摇臂**

怎样折中

在探索与利用之间进行折中

• Epsilon greedy
• Softmax
  简单解释一下 $ϵ$贪心就是 以一个较小的概率$ϵ$进行探索，随机选择摇臂来拉。而以一个较大的概率$1-ϵ$进行利用，选择目前为止我们认为最好的那个摇臂。目前为止我们认为最好：就是这么多次尝试之后，记录每个摇臂的平均reward咯。
  一般改进一下会效果更好，就是刚开始时候，估计的每个摇臂的平均reward是很不准确的，因此应该多探索。后面估计的越来越准确了，则要多利用，因此把$ϵ$设置为一个随着玩的次数增多而逐渐递减的数，而不是固定值。

Softmax算法也类似，其中$\tau$称为“温度”，越小就表示平均reward高的那个摇臂被选去的概率高。

进入算法

准备工作1

用变量来替代上面的语言～～
每个摇臂的平均奖赏：
value of action $a$： $q_{\ast }(a)$
q∗(a)=E[Rt∣At=a]q_*(a)=E[R_t|A_t=a]