一、基于图像梯度(空域)
正焦的清晰图像比模糊的离焦图像边缘更加锐利清晰,边缘像素灰度值变化大,因而有更大的梯度值。在进行图像处理时,将图像看作二维离散矩阵,利用梯度函数获取图像灰度信息,以此来评判图像清晰度。在离散信号中梯度表现为差分形式。常用的梯度函数有:能量梯度函数EOG、Roberts函数、Tenengrad函数、Brenner函数、方差Variance函数、拉普拉斯Laplace函数等等。下面分别对其进行介绍。
1、Tenengrad 梯度函数
Tenengrad梯度函数是一种基于图像的边缘信息,通过计算图像中边缘的梯度变化来评估图像的清晰度。边缘信息通常与图像中的高频成分相关,因此,边缘的强度和数量可以作为图像清晰度的指标。
在Tenengrad算法中,首先会对图像应用Sobel等边缘检测算子来检测边缘。然后,计算检测到的边缘的梯度幅值,并对这些幅值进行统计,得到一个表示图像清晰度的度量。通常,边缘梯度幅值的总和或平均值可以作为清晰度评价指标,数值越大说明图像越清晰。
方法存在的缺点:
对噪声敏感:由于Tenengrad梯度函数主要依赖图像的边缘信息,因此它对噪声非常敏感。图像中的噪声可能会导致边缘检测的不准确,进而影响清晰度评价的准确性。
计算复杂度高:为了计算梯度幅值,Tenengrad方法需要对每个像素点应用边缘检测算子,并进行相应的数学运算。因此,在处理大规模图像或实时应用时,计算复杂度可能会成为瓶颈,影响处理速度。
参数依赖性:Tenengrad方法的性能可能受到所选参数的影响,如边缘检测算子的类型和大小。选择合适的参数对于获得准确的清晰度评价至关重要,但这也增加了算法的复杂性和调参的难度。
边缘信息局限性:虽然边缘信息对于评估图像清晰度很重要,但它并不能完全反映图像的所有特征。有些图像可能具有丰富的纹理信息而不是明显的边缘,这种情况下,Tenengrad方法可能无法准确评估图像的清晰度。
c++程序实现:
#include <opencv2/opencv.hpp>
#include <cmath>
#include <iostream>
double calculateTenengrad(const cv::Mat& img) {
cv::Mat grayImg;
if (img.channels() == 3) {
cv::cvtColor(img, grayImg, cv::COLOR_BGR2GRAY);
} else {
grayImg = img;
}
cv::Mat grad_x, grad_y;
// 使用Sobel算子计算x和y方向的梯度
cv::Sobel(grayImg, grad_x, CV_32F, 1, 0, 3);
cv::Sobel(grayImg, grad_y, CV_32F, 0, 1, 3);
// 计算梯度幅值
cv::Mat grad_mag;
cv::cartToPolar(grad_x, grad_y, grad_mag, cv::Mat(), true);
// 计算梯度幅值的总和作为清晰度评价
double sum = cv::sum(grad_mag)[0];
return sum;
}
int main() {
cv::Mat img = cv::imread("path_to_your_image.jpg", cv::IMREAD_COLOR);
if (img.empty()) {
std::cerr << "Error: Could not read the image." << std::endl;
return -1;
}
double tenengrad = calculateTenengrad(img);
std::cout << "Tenengrad Score: " << tenengrad << std::endl;
return 0;
}
2、 Laplacian梯度函数
Laplacian 梯度函数与Tenengrad梯度函数基本一致,用Laplacian算子替代Sobel算子即可。Laplacian 梯度函数基于图像的二阶导数信息来评估图像的清晰度。对图像中的边缘和突变点非常敏感,因此可以用来衡量图像的细节丰富程度和清晰度。
Laplacian梯度函数通过计算图像的Laplacian算子得到图像的梯度信息。在理想情况下,清晰图像的Laplacian响应(即梯度值的绝对值之和或平方和)应该比模糊图像更大。数值越大图像越清晰。
方法存在的缺点:
噪声敏感性:Laplacian算子对噪声非常敏感,因为噪声通常表现为高频成分,这可能导致清晰度评价的准确性降低。
边缘信息损失:Laplacian算子在检测边缘时,可能会丢失一些边缘信息,尤其是在边缘较宽或梯度变化平缓的情况下。
局部性质:Laplacian算子只关注图像的局部变化,对于全局性的清晰度评价可能不够准确。
阈值选择:在实际应用中,需要设定一个阈值来判断图像的清晰度,而这个阈值的选择可能需要根据具体的应用场景进行调整。
c++程序实现:
#include <opencv2/opencv.hpp>
#include <iostream>
double calculateLaplacianGradient(const cv::Mat& img) {
cv::Mat grayImg;
if (img.channels() == 3) {
cv::cvtColor(img, grayImg, cv::COLOR_BGR2GRAY);
} else {
grayImg = img;
}
cv::Mat laplacianImg;
cv::Laplacian(grayImg, laplacianImg, CV_64F);
// 计算Laplacian响应的绝对值之和作为清晰度评价
double sumAbs = cv::sum(cv::abs(laplacianImg))[0];
return sumAbs;
}
int main() {
cv::Mat img = cv::imread("path_to_your_image.jpg", cv::IMREAD_COLOR);
if (img.empty()) {
std::cerr << "Error: Could not read the image." << std::endl;
return -1;
}
double laplacianScore = calculateLaplacianGradient(img);
std::cout << "Laplacian Gradient Score: " << laplacianScore << std::endl;
return 0;
}
3、SMD(灰度差分绝对值之和)函数
SMD是用于计算两幅图像或同一图像不同区域之间差异的方法。其基本原理是逐像素地计算两幅图像的灰度值差异,并将所有差异的绝对值求和。这种方法简单直观,计算效率高,适用于需要快速比较图像相似性的场合,数值越大图像越清晰。公式如下:

方法存在的缺点:
对噪声敏感:由于SMD是基于像素级的差异计算,因此它对图像中的噪声非常敏感。即使是很小的噪声也可能导致较大的SMD值,从而影响对图像差异的判断。
忽略空间信息:SMD方法只考虑了像素值之间的差异,而没有考虑像素之间的空间关系。这意味着即使两幅图像的内容完全不同,但只要它们的像素值分布相似,SMD值也可能很小。
对缩放、旋转等变换不鲁棒:如果两幅图像之间存在缩放、旋转等几何变换,那么即使它们的内容相似,SMD值也可能很大。这是因为这些变换会改变像素的空间位置,导致对应像素的灰度值差异增大。
计算效率受图像大小影响:虽然SMD方法的计算效率相对较高,但当处理大尺寸图像时,由于需要遍历图像中的每一个像素,因此计算时间可能会显著增加。
c++程序实现:
#include <iostream>
#include <vector>
#include <cmath>
using namespace std;
// 假设我们有一个简单的灰度图像表示,使用二维vector存储像素值
typedef vector<vector<unsigned char>> GrayImage;
// 计算两幅灰度图像的SMD值
int calculateSMD(const GrayImage& image1, const GrayImage& image2) {
int width = image1.size();
int height = image1[0].size();
int smd = 0;
// 遍历图像中的每一个像素
for (int y = 0; y < height; ++y) {
for (int x = 0; x < width; ++x) {
// 计算两个图像在对应像素位置上的灰度值之差,并取绝对值
int diff = abs(static_cast<int>(image1[x][y]) - static_cast<int>(image2[x][y]));
// 将差值累加到SMD中
smd += diff;
}
}
return smd;
}
int main() {
// 创建两幅示例灰度图像(这里仅为示例,实际使用时需要加载或生成图像数据)
GrayImage image1 = {{10, 20, 30}, {40, 50, 60}};
GrayImage image2 = {{11, 19, 31}, {41, 49, 59}};
// 计算SMD值并输出
int smd = calculateSMD(image1, image2);
cout << "SMD: " << smd << endl;
return 0;
}
4、SMD2 (灰度方差乘积)函数
SMD2算法通过计算图像中相邻像素的灰度值差异,并将这些差异进行乘积运算,然后求和,从而得到一个反映图像清晰度的指标。数值越大图像越清晰。
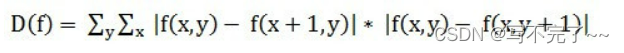
c++程序实现:
#include <iostream>
#include <vector>
#include <cmath>
float SMD2(std::vector<std::vector<int>>& img) {
int shape_x = img.size();
int shape_y = img[0].size();
float out = 0;
for (int x = 0; x < shape_x - 1; x++) {
for (int y = 0; y < shape_y - 1; y++) {
out += std::abs(img[x][y] - img[x + 1][y]) * std::abs(img[x][y] - img[x][y + 1]);
}
}
return out;
}
int main() {
// 示例图像,可以根据实际情况修改
std::vector<std::vector<int>> img = {{1, 2, 3},
{4, 5, 6},
{7, 8, 9}};
float result = SMD2(img);
std::cout << "SMD2结果为: " << result << std::endl;
return 0;
}
5、EOG(能量梯度)函数
EOG(Energy of Gradient)算法是一种基于图像梯度信息的清晰度评价方法。它通过计算图像中像素灰度值的变化率(即梯度)来评估图像的清晰度。EOG算法认为,清晰度高的图像在边缘和纹理区域应该具有较大的灰度变化,即较大的梯度值。
在EOG算法中,首先计算图像中每个像素在水平和垂直方向上的梯度值。这通常通过卷积运算实现,使用预先定义的梯度算子(如Prewitt算子、Sobel算子等)与图像进行卷积。然后,将每个像素的梯度值进行平方并求和,得到整个图像的梯度能量。这个梯度能量值就作为评价图像清晰度的指标。数值越大图像越清晰。
c++程序实现:
#include <iostream>
#include <vector>
#include <cmath>
#include <opencv2/opencv.hpp>
using namespace std;
using namespace cv;
double computeGradientEnergy(const Mat& image) {
Mat grad_x, grad_y;
double gradientEnergy = 0.0;
// 计算图像在x和y方向上的梯度
Sobel(image, grad_x, CV_64F, 1, 0, 3); // 水平方向梯度
Sobel(image, grad_y, CV_64F, 0, 1, 3); // 垂直方向梯度
// 计算梯度能量的和
for (int y = 0; y < image.rows; ++y) {
for (int x = 0; x < image.cols; ++x) {
double grad_mag = sqrt(grad_x.at<double>(y, x) * grad_x.at<double>(y, x) +
grad_y.at<double>(y, x) * grad_y.at<double>(y, x));
gradientEnergy += grad_mag * grad_mag; // 计算梯度能量的平方和
}
}
return gradientEnergy;
}
int main() {
// 读取图像
Mat image = imread("path_to_image.jpg", IMREAD_GRAYSCALE);
if (image.empty()) {
cerr << "Error: Unable to load image." << endl;
return -1;
}
// 计算图像的梯度能量
double gradientEnergy = computeGradientEnergy(image);
cout << "Gradient Energy: " << gradientEnergy << endl;
return 0;
}
6、Roberts函数
Roberts函数是一种基于梯度信息的图像清晰度评价算法。它利用Roberts算子来计算图像中每个像素点在水平和垂直方向上的梯度,并通过这些梯度值来评估图像的清晰度。Roberts算子是一种简单的2x2梯度算子,对图像进行卷积运算后,可以得到图像中每个像素点处边缘的强度。
具体来说,Roberts算子包括两个2x2的矩阵,分别用于计算水平和垂直方向上的梯度。通过将这两个矩阵与图像的每个2x2像素块进行卷积,可以得到水平和垂直方向上的梯度值。然后,可以将这两个梯度值结合起来,比如取它们的平方和作为该像素点的梯度强度。最后,对所有像素点的梯度强度进行求和或平均,得到整个图像的清晰度评价指标。
该方法的抗干扰能力较差。当用该算法对边缘灰度值变换缓慢的目标图像(例如白云,海滩)做清晰度评价时,很难识别边缘,算法性能较差。
方法存在的缺点:
对噪声敏感:由于Roberts算子只考虑了相邻像素的差异,它对噪声非常敏感。噪声会引入虚假的边缘,从而影响清晰度的评价结果。
边缘定位精度不高:Roberts算子是一个简单的2x2算子,它在边缘定位上可能不够精确,特别是在边缘较宽或复杂的情况下。
无法区分不同方向的边缘:Roberts算子只能计算水平和垂直方向上的梯度,对于其他方向的边缘可能不够敏感。
对图像尺寸和内容的依赖:Roberts方法的评价结果可能受到图像尺寸和内容的影响,不同尺寸的图像或具有不同纹理和细节的图像可能产生不同的评价结果。
#include <opencv2/opencv.hpp>
#include <iostream>
using namespace cv;
using namespace std;
Mat computeRobertsGradient(const Mat& image) {
Mat grad_x, grad_y, abs_grad_x, abs_grad_y, gradient;
grad_x = Mat::zeros(image.size(), CV_32F);
grad_y = Mat::zeros(image.size(), CV_32F);
// Roberts算子
const int gx[2][2] = {{1, 0}, {0, -1}};
const int gy[2][2] = {{0, 1}, {-1, 0}};
// 计算水平和垂直方向的梯度
filter2D(image, grad_x, CV_32F, gx);
filter2D(image, grad_y, CV_32F, gy);
// 取绝对值
convertScaleAbs(grad_x, abs_grad_x);
convertScaleAbs(grad_y, abs_grad_y);
// 计算梯度强度(梯度幅值)
addWeighted(abs_grad_x, 0.5, abs_grad_y, 0.5, 0, gradient);
return gradient;
}
int main() {
// 读取图像
Mat image = imread("path_to_image.jpg", IMREAD_GRAYSCALE);
if (image.empty()) {
cerr << "Error: Unable to load image." << endl;
return -1;
}
// 计算Roberts梯度
Mat gradient = computeRobertsGradient(image);
// 显示梯度图像(可选)
imshow("Gradient", gradient);
waitKey(0);
// 在这里,您可以进一步处理gradient来计算清晰度评价指标
// ...
return 0;
}
7、Brenner梯度函数
Brenner梯度函数是最简单的梯度评价函数。它通过对图像中相邻像素的灰度值进行差分运算,然后计算差分的平方和来评估图像的清晰度。这种方法主要依据图像的边缘信息来判断图像的清晰程度。
具体来说,Brenner梯度函数计算图像中每个像素与其水平方向上相邻像素的灰度差值的平方,然后将所有像素的差值平方和作为图像的清晰度评价指标。这个指标越大,通常表示图像的清晰度越高。
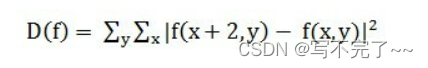
方法存在的缺点:
对噪声敏感:和许多基于梯度的清晰度评价方法一样,Brenner梯度函数对图像中的噪声非常敏感。噪声会导致灰度值的随机波动,从而影响梯度计算的准确性。
方向性:Brenner梯度函数主要关注水平方向的梯度变化,因此对于垂直方向或对角线方向的边缘可能不够敏感。这可能导致在某些情况下无法准确评估图像的清晰度。
局部性:Brenner梯度函数只考虑了相邻像素之间的灰度差异,因此它只能提供局部清晰度的信息,而不能反映整个图像的清晰度分布情况。
阈值设定:在实际应用中,需要设定一个阈值来判断图像的清晰度是否满足要求。然而,这个阈值的设定往往需要根据具体的应用场景和图像特点进行调整,缺乏通用性。
#include <iostream>
#include <vector>
#include <cmath>
#include <opencv2/opencv.hpp>
using namespace cv;
using namespace std;
double computeBrennerGradient(const Mat& image) {
int width = image.cols;
int height = image.rows;
double sum = 0.0;
// 遍历图像中的每个像素(除了最左边的列)
for (int i = 0; i < height; ++i) {
for (int j = 1; j < width; ++j) {
// 计算相邻像素的水平方向梯度差的平方
int diff = static_cast<int>(image.at<uchar>(i, j)) - static_cast<int>(image.at<uchar>(i, j - 1));
sum += diff * diff;
}
}
// 返回梯度平方和作为清晰度指标
return sum;
}
int main() {
// 读取图像
Mat image = imread("path_to_image.jpg", IMREAD_GRAYSCALE);
if (image.empty()) {
cerr << "Error: Unable to load image." << endl;
return -1;
}
// 计算Brenner梯度
double brennerGradient = computeBrennerGradient(image);
// 输出清晰度指标
cout << "Brenner Gradient: " << brennerGradient << endl;
// 在这里,您可以根据布伦纳梯度值来判断图像的清晰度,并进行相应的处理
return 0;
}
二、基于信息熵
1、 Entropy(信息熵)函数
基于统计特征的熵函数是衡量图像信息丰富程度的一个重要指标,有信息论可知,一幅图像 f 的信息量是由该图像的信息熵 D(f) 来度量:
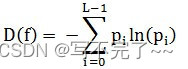
其中:Pi 是图像中灰度值为i的像素出现的概率,L为灰度级总数(通常取值256)。
在图像处理中,特别是用于评估图像清晰度时,信息熵可以被用来量化图像灰度级别的分布。如果图像的灰度分布均匀,则信息熵较高,意味着图像包含较多的信息;反之,如果灰度分布集中在某一特定范围,则信息熵较低,图像信息含量较少,可能意味着图像模糊。熵函数灵敏度不高,依据图像内容不同容易出现与真实情况相反的结果。
c++程序实现:
#include <opencv2/opencv.hpp>
#include <cmath>
#include <iostream>
#include <vector>
double calculateEntropy(const cv::Mat& img) {
cv::Mat grayImg;
if (img.channels() == 3) {
cv::cvtColor(img, grayImg, cv::COLOR_BGR2GRAY);
} else {
grayImg = img;
}
std::vector<float> histogram;
int histSize = 256;
float range[] = { 0, 256 };
const float* histRange = { range };
cv::calcHist(&grayImg, 1, 0, cv::Mat(), histogram, 1, &histSize, &histRange);
// Normalize histogram to get probabilities
double sum = cv::sum(histogram)[0];
if (sum > 0) {
for (int i = 0; i < histSize; ++i) {
histogram[i] /= sum;
}
} else {
std::cerr << "Error: Sum of histogram is zero." << std::endl;
return 0.0;
}
double entropy = 0.0;
for (size_t i = 0; i < histogram.size(); ++i) {
double p = histogram[i];
if (p > 0) {
entropy -= p * log2(p);
}
}
return entropy;
}
int main() {
cv::Mat img = cv::imread("path_to_your_image.jpg", cv::IMREAD_COLOR);
if (img.empty()) {
std::cerr << "Error: Could not read the image." << std::endl;
return -1;
}
double entropy = calculateEntropy(img);
std::cout << "Image Entropy: " << entropy << std::endl;
return 0;
}
三、基于频域
1、二维离散傅里叶变换(DFT)函数
在频率域中,图像的信息被表示为不同频率成分的组合,这使得我们可以更容易地分析和处理图像的某些特性,如边缘、纹理和周期性结构。
对于清晰度评价,DFT的主要思想是:清晰的图像在频率域中应该有更多的高频成分,因为高频成分通常与图像的细节和边缘相关。因此,通过计算图像的DFT并分析高频分量的强度,可以对图像的清晰度进行评估。数值越大图像越清晰。

方法存在的缺点:
计算复杂性:DFT的计算复杂度较高,特别是对于大尺寸的图像。这可能导致实时应用中的性能问题。
对噪声的敏感性:DFT对图像中的噪声非常敏感。噪声在频率域中表现为高频分量,这可能会干扰对图像清晰度的准确评估。
高频分量不一定代表清晰度:虽然高频分量通常与图像的细节和边缘相关,但并非所有高频分量都代表清晰度。例如,图像的纹理和噪声也会在频率域中产生高频分量。
缺乏直观的清晰度指标:DFT提供的是频率域的信息,而不是直接的清晰度指标。因此,需要进一步的处理和分析才能将DFT的结果转换为清晰度评价指标。
#include <opencv2/opencv.hpp>
#include <iostream>
#include <complex>
using namespace cv;
using namespace std;
Mat computeDFT(const Mat& image) {
Mat planes[] = {Mat_<float>(image), Mat::zeros(image.size(), CV_32F)};
Mat complexI;
merge(planes, 2, complexI);
Mat dft;
dft(complexI, dft, DFT_COMPLEX_OUTPUT);
split(dft, planes);
magnitude(planes[0], planes[1], planes[0]);
Mat magI = planes[0];
magI += Scalar::all(1);
log(magI, magI);
normalize(magI, magI, 0, 1, NORM_MINMAX);
return magI;
}
int main() {
// 读取图像
Mat image = imread("path_to_image.jpg", IMREAD_GRAYSCALE);
if (image.empty()) {
cerr << "Error: Unable to load image." << endl;
return -1;
}
// 计算DFT
Mat dftResult = computeDFT(image);
// 显示原始图像和DFT结果
imshow("Original Image", image);
imshow("DFT Result", dftResult);
waitKey(0);
return 0;
}
2、离散余弦变换(DCT)函数
离散余弦变换(DCT)是一种实数域变换,与DFT相比,它在图像和视频压缩等领域有着广泛的应用。DCT的基本思想是将信号(在这里是图像的灰度值)分解为一组不同频率的余弦函数之和。这些余弦函数的频率逐渐增高,并且幅度(即系数)表示了原始信号中对应频率分量的强度。
在清晰度评价中,DCT可以被用来分析图像中不同频率分量的分布。理论上,一个清晰的图像应该包含较多的高频分量,因为高频分量通常与图像的细节和边缘相关。因此,DCT系数中高频分量的能量或幅度可以被用作评价图像清晰度的指标。
方法存在的缺点:
计算复杂性:虽然DCT的计算复杂性比DFT低一些,但对于大尺寸的图像,DCT的计算仍然可能相对耗时。
高频噪声敏感性:和DFT一样,DCT也对图像中的高频噪声敏感。噪声的存在可能会干扰对图像清晰度的准确评估。
缺乏直观的清晰度指标:DCT提供的是变换域的信息,需要进一步的处理和分析才能转换为直观的清晰度指标。
可能不适用于所有类型的图像:某些类型的图像(如模糊图像或具有大量均匀区域的图像)可能不适合用DCT进行清晰度评价,因为这些图像在DCT变换后可能没有明显的高频分量
#include <opencv2/opencv.hpp>
#include <iostream>
#include <vector>
using namespace cv;
using namespace std;
Mat computeDCT(const Mat& image) {
Mat dct;
// 将图像转换为单通道灰度图像
Mat gray;
cvtColor(image, gray, COLOR_BGR2GRAY);
// 对图像进行DCT变换
dct(gray, dct, DCT_NORM_SCALED);
// 可以根据需要进一步处理DCT系数,例如计算高频分量的能量等
// ...
return dct;
}
int main() {
// 读取图像
Mat image = imread("path_to_image.jpg");
if (image.empty()) {
cerr << "Error: Unable to load image." << endl;
return -1;
}
// 计算DCT
Mat dctResult = computeDCT(image);
// 显示原始图像和DCT结果(这里仅显示DCT系数矩阵的绝对值,因为DCT可能包含负数)
imshow("Original Image", image);
Mat dctAbs;
absdiff(dctResult, Scalar::all(0), dctAbs); // 计算DCT系数的绝对值
normalize(dctAbs, dctAbs, 0, 255, NORM_MINMAX, CV_8UC1); // 归一化到0-255范围并转换为8位无符号整数类型
imshow("DCT Result (Absolute Values)", dctAbs);
waitKey(0);
return 0;
}
四、基于统计学
1、自相关(Vollaths)函数
Vollaths函数反映空间两点的相似性。正焦图像边缘清晰锐利,像素点之间相关程度低;离焦图像像素点相关程度高。清晰度评价函数如下所示:
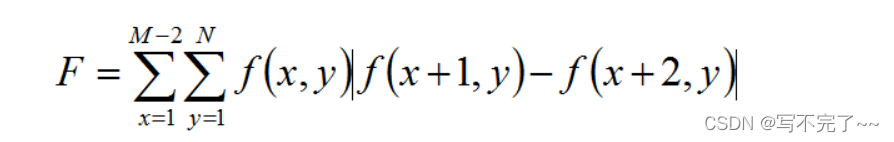
#include <iostream>
#include <vector>
#include <cmath>
std::vector<double> computeAutocorrelation(const std::vector<double>& signal) {
int N = signal.size();
std::vector<double> autocorrelation(N, 0.0);
for (int tau = 0; tau < N; ++tau) {
for (int t = 0; t <= N - tau - 1; ++t) {
autocorrelation[tau] += signal[t] * signal[t + tau];
}
autocorrelation[tau] /= N - tau; // 归一化
}
return autocorrelation;
}
int main() {
std::vector<double> signal = {1, 2, 3, 2, 1}; // 示例信号
std::vector<double> autocorr = computeAutocorrelation(signal);
std::cout << "Autocorrelation:" << std::endl;
for (double val : autocorr) {
std::cout << val << " ";
}
std::cout << std::endl;
return 0;
}
小结
各方法主要思想如下:
图像模糊这一特点在空域中表现为相邻像素间的特征值如灰度、纹理、颜色等在离焦时大小发生变化,因此可以采用图像的梯度信息作为图像清晰度评价依据。
图像模糊时损失大量的高频信息,因此可以依据高频信息的多少来判断离焦程度。对图像进行变换域处理之后,提取其中的高频分量作为图像清晰度函数。
不同清晰度的图像就会形成不同的光能量分布,图像越模糊,相邻像素之间的影响就越大,导致图像的光能量分布更趋于平均分布。
清晰的图像具有更多的细节信息,在灰度上的表现就是灰度分布的直方图集中度低,灰度范围大,反过来说,图像越模糊,灰度越向均值附近集中,灰度范围逐渐变小。
参考链接:
https://blog.youkuaiyun.com/jzwong/article/details/113823821
https://blog.youkuaiyun.com/zsk444/article/details/122985940




















 195
195










