1.概述
是一个可以并行执行任务的线程池。可以处理一个可递归划分的任务并获取结果(分而治之的思想,父任务等待子任务执行完成并组装结果)。因为是多线程去执行任务,可以充分利用多核,提高cpu的利用率。那么他如何做构建管理任务队列,多线程如何去处理任务,以及他的应用场景和性能瓶颈是什么?通过下面原理以及源码我们来进一步了解。
2.Fork/Join介绍
为分治算法的并行实现。
Result solve(Problem problem) {
if (problem is small)
directly solve problem
else {
split problem into independent parts
fork new subtasks to solve each part
join all subtasks
compose result from subresults
}
}
fork操作会启动一个新的任务。而join则是等待该任务阻塞完成。
如果问题较大。我们只需要将问题分解。fork出去,然后通过join等待结果,最后计算结果返回。这里有个问题就是大部分任务做的事情就是分解任务,然后等待子任务执行。
3.数据结构
1.会创建一个Worker线程池,每个线程用来处理队列中的任务。
2.所有的任务都是一个轻量级可执行的类(ForkJoinTask)。任务的方法就在工作线程运行的时候被调用处理。
工作窃取
对于CPU,重要的可能就是进程和线程的调度。但是对于上层,考虑的应该是如何充分利用线程资源。这就需要进行合理的任务(工作量)调度。
对于工作窃取调度策略实现如下:
- 每个线程都有自己的任务队列。
- 队列是一个双端队列,可以 前后取
- Fork的子任务只会被丢进所在线程的队列
- 工作线程通过LIFO获取任务
- 任务队列没有任务,会尝试随机窃取一个队列的任务执行。FIFO
- 工作线程调用join的时候,线程并不会阻塞,而是会去处理其他队列的任务。直到当前任务执行完成,返回结果
- 如果工作线程没有任务处理(自己队列无任务,并且没有窃取到任务),会让其让出资源。阻塞线程。等待后续激活。对于工作线程会有一个顶层线程去激活它。
工作线程获取自己队列任务和窃取别人任务的方式不同。这能减少竞争。
fork采用LIFO,这保证了队列头部任务都会是更大的任务,尾部是分解出来的子任务。窃取采用FIFO,窃取更大的任务有助于本次窃取的性价比很高。
如上所述,ForkJoinPool有一个WorkQueue数组。每个数组的元素是一个双端队列(Dqueue)。WorkQueue主要用来存储需要执行的任务。
需要注意的一点是,线程对应的WorkQueue在数组的下标都是奇数。那么大家会问,偶数索引对应的WorkQueue是什么。其实是用来存储直接向ForkJoinPool提交的(外部提交)任务。
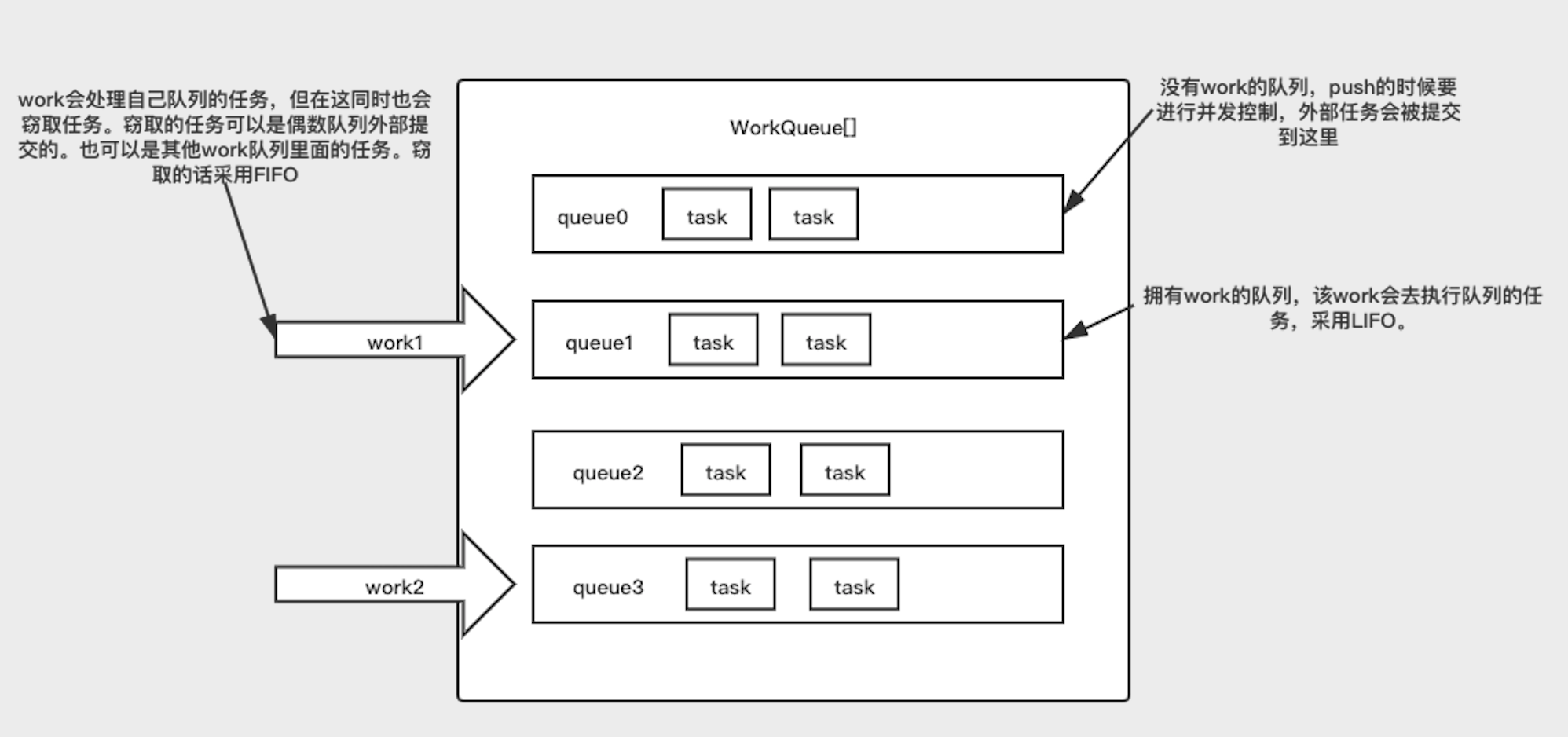
双端队列
需要考虑的是队列的并发控制。
双端队列采用数组的形式,维护了一个top和base的指针。push、pop、take操作都会通过移动指针去维护。对于push和pop都是同一个线程去执行。所以不会有并发问题。take窃取过程可能会有多线程操作。所以需要加锁。
那么核心问题就是解决队列元素不足时pop、push和take的冲突。
通过volatile的top和base指针。我们可以计算出队列元素数量。显然当数量大于1的时候。不冲突。
对于pop操作会先递减top:if(–top) >= base) …
对于take操作先递增base:if(++base < top) …
我们只需要比较这两个索引来检测是否会导致队列为空。对于pop,如果可能导致为空,加锁再判断。然后根据结果进行对应逻辑。如果是take。直接回退。不需要二次判断。
4.跟踪源码
通过上面介绍,我们了解线程如何获取任务。要进一步了解我们就需要深入到源代码中。首先我们用一个测试程序来进行分析。
public class ForkJoinCalculator {
private ForkJoinPool pool;
public ForkJoinCalculator() {
// 也可以使用公用的 ForkJoinPool:
// pool = ForkJoinPool.commonPool()
pool = new ForkJoinPool();
}
public long sumUp(long[] numbers) {
return pool.invoke(new SumTask(numbers, 0, numbers.length - 1));
}
private static class SumTask extends RecursiveTask<Long> {
private long[] numbers;
private int from;
private int to;
public SumTask(long[] numbers, int from, int to) {
this.numbers = numbers;
this.from = from;
this.to = to;
}
@Override
protected Long compute() {
// 当需要计算的数字小于6时,直接计算结果
if (to - from < 6) {
long total = 0;
for (int i = from; i <= to; i++) {
total += numbers[i];
}
return total;
// 否则,把任务一分为二,递归计算
} else {
int middle = (from + to) / 2;
SumTask taskLeft = new SumTask(numbers, from, middle);
SumTask taskRight = new SumTask(numbers, middle + 1, to);
taskLeft.fork();
taskRight.fork();
return taskLeft.join() + taskRight.join(







 ForkJoinPool是Java中实现并发任务的一种高效工具,基于分治策略,利用工作窃取算法来充分利用多核CPU。本文深入探讨了ForkJoinPool的工作原理,包括数据结构中的双端队列、任务的Fork与Join操作,以及源码跟踪分析,展示了ForkJoinPool如何通过线程间任务窃取实现负载均衡,与ThreadPoolExecutor的区别及其适用场景。
ForkJoinPool是Java中实现并发任务的一种高效工具,基于分治策略,利用工作窃取算法来充分利用多核CPU。本文深入探讨了ForkJoinPool的工作原理,包括数据结构中的双端队列、任务的Fork与Join操作,以及源码跟踪分析,展示了ForkJoinPool如何通过线程间任务窃取实现负载均衡,与ThreadPoolExecutor的区别及其适用场景。
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章

















 847
847

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








