236 Lowest Common Ancestor of a Binary Tree

最新推荐文章于 2024-10-16 01:06:12 发布

weixin_39145266

最新推荐文章于 2024-10-16 01:06:12 发布

阅读量76

点赞数

CC 4.0 BY-SA版权

分类专栏： LeetCode # Medium # Solved # Tree

本文链接：https://blog.youkuaiyun.com/weixin_39145266/article/details/89473235

LeetCode 同时被 3 个专栏收录

200 篇文章

订阅专栏

Medium

178 篇文章

订阅专栏

Solved

160 篇文章

订阅专栏

本文探讨了在二叉树中寻找两个节点的最低公共祖先(LCA)的问题，提供了两种解决方案：一种是通过记录每个节点的父亲节点路径，然后比较路径找到公共祖先；另一种是递归遍历树，直接返回LCA。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

1 题目

Given a binary tree, find the lowest common ancestor (LCA) of two given nodes in the tree.

According to the definition of LCA on Wikipedia: “The lowest common ancestor is defined between two nodes p and q as the lowest node in T that has both p and q as descendants (where we allow a node to be a descendant of itself).”

Given the following binary tree:  root = [3,5,1,6,2,0,8,null,null,7,4]

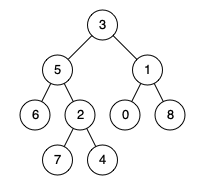
Example 1:

Input: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
Output: 3
Explanation: The LCA of nodes 5 and 1 is 3.

Example 2:

Input: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4
Output: 5
Explanation: The LCA of nodes 5 and 4 is 5, since a node can be a descendant of itself according to the LCA definition.

2 尝试解

class Solution {
public:
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        vector<TreeNode*> father_p,father_q,temp;
        findFather(root,p,temp,father_p);
        temp.clear();
        findFather(root,q,temp,father_q);
        for(int i = 0; i < father_q.size() && i < father_p.size(); i++){
            if(i == father_q.size()-1 || i == father_p.size()-1 || father_p[i+1] != father_q[i+1]) return father_p[i];
        }
        return root;
    }
    void findFather(TreeNode* root,TreeNode* target,vector<TreeNode*>&temp,vector<TreeNode*>&result){
        if(root == NULL) return;
        temp.push_back(root);
        if(root == target) {
            result = temp; return;
        }
        if(root->left != NULL){
            findFather(root->left,target,temp,result);
        }
        if(root->right != NULL){
            findFather(root->right,target,temp,result);
        }
        temp.pop_back();
    }
};

3 标准解

TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
    if (!root || root == p || root == q) return root;
    TreeNode* left = lowestCommonAncestor(root->left, p, q);
    TreeNode* right = lowestCommonAncestor(root->right, p, q);
    return !left ? right : !right ? left : root;
}