数据结构——2-3-4树

1 引言

在上一篇文章中介绍了2-3树的定义以及插入删除操作。本篇文章将在2-3树的基础上更进一步，介绍比2-3树更为复杂的数据结构2-3-4树。之所以介绍2-3-4树是因为2-3-4树与极为重要的红黑树有着等价关系，通过先学习2-3-4树为后面学习红黑树打下基础，增进对于红黑树的理解。

2 2-3-4树

2-3树不再是单纯的二叉树了，因为2-3树中除了2-节点之外还存在3-节点。在2-3树的基础上进一步扩展，2-3-4树在2-3树的基础上添加4-节点。4-节点可以存储3个键值，最多可以拥有4棵子树。

3 定义

（1）每个节点每个节点有1、2或3个key，分别称为2-节点，3-节点，4-节点。
（2）所有叶子节点到根节点的长度一致（也就是说叶子节点都在同一层）。
（3）每个节点的key从左到右保持了从小到大的顺序，两个key之间的子树中所有的 key一定大于它的父节点的左key，小于父节点的右key。

例如：图3.1所示的一棵2-3-4树。其中，有5个2-节点，2个3-节点和1个4-节点。

图3.1

4 查找

2-3-4树的查找类似了二叉树的查找过程，通过键值的比较来决定遍历方向。

例如：在图3.1所示树中查找key为22的节点。

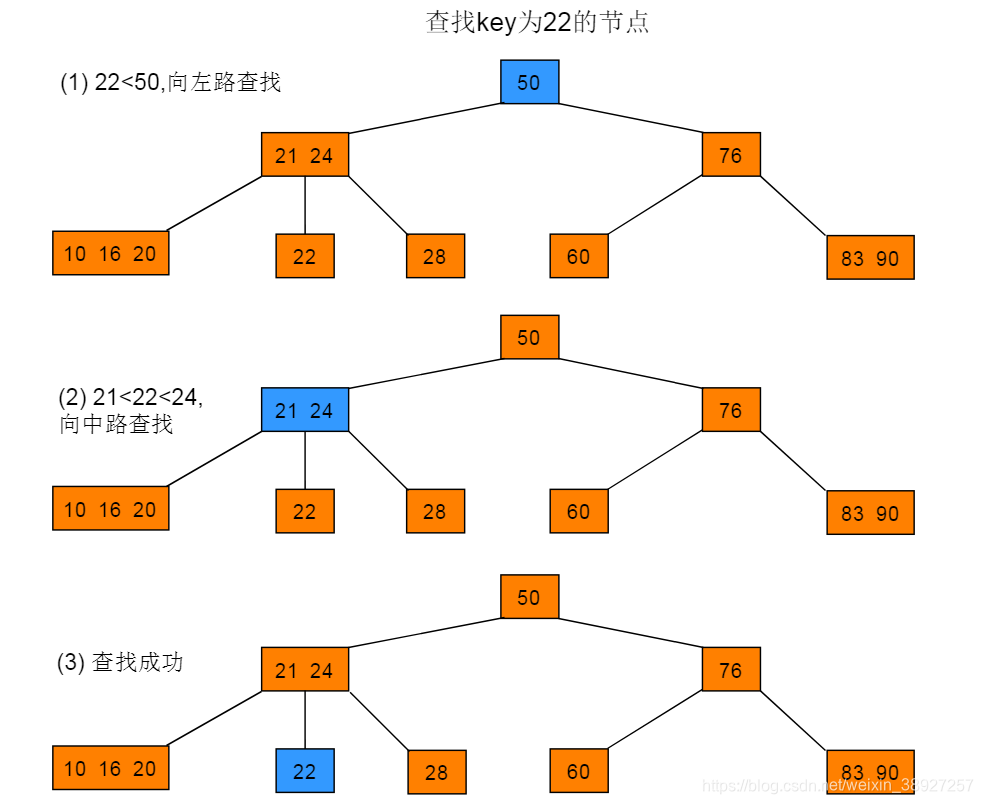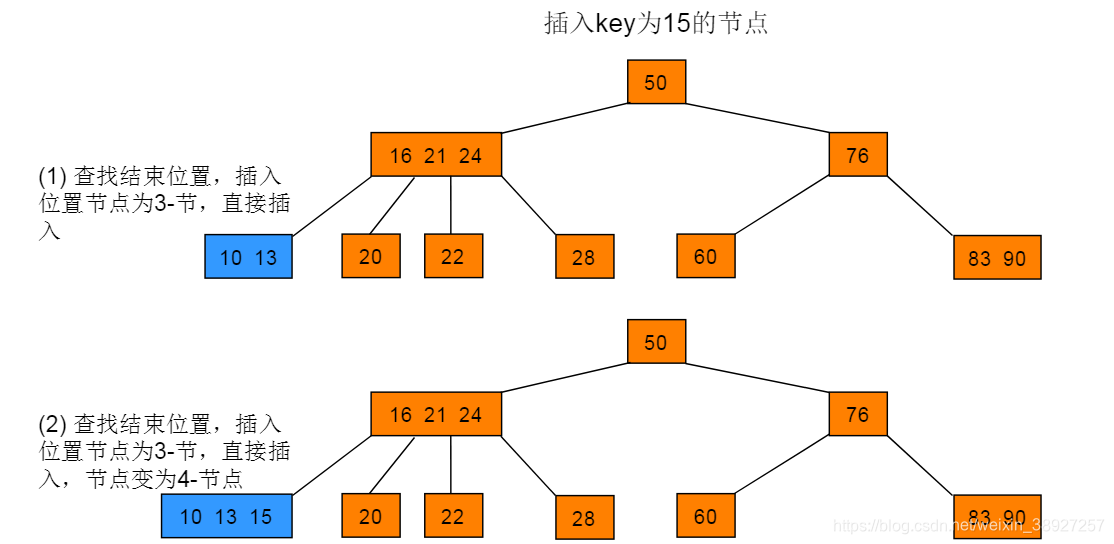
例如：在图3.1所示树中查找key为15的节点。

5 插入

如果2-3-4树中已存在当前插入的key，则插入失败，否则最终一定是在叶子节点中进行插入操作，因为查找过程的结束位置在叶子节点。节点的插入主要有以下几种情形：

5.1 非4-节点插入

插入步骤：如果待插入的节点不是4-节点，那么直接在该节点插入。

例如：在2-节点插入key为62的节点：
图解

例如：在3-节点插入key为94的节点：
图解

5.2 4-节点插入

插入步骤：如果待插入的节点是个4-节点，那么应该先分裂该节点然后再插入。一个4-节点可以分裂成一个根节点和两个子节点（这三个节点各含一个key）然后在子节点中插入，我们把分裂形成的根节点中的key看成向上层插入的key，然后重复5.1和5.2。

图解：

5.3 父节点分裂

如果是在4节点中进行插入，每次插入会多出一个分支，如果插入操作导致父节点分裂。若插入节点，导致根节点发生分裂，则2-3-4树会生长一层。

图解：

6 删除

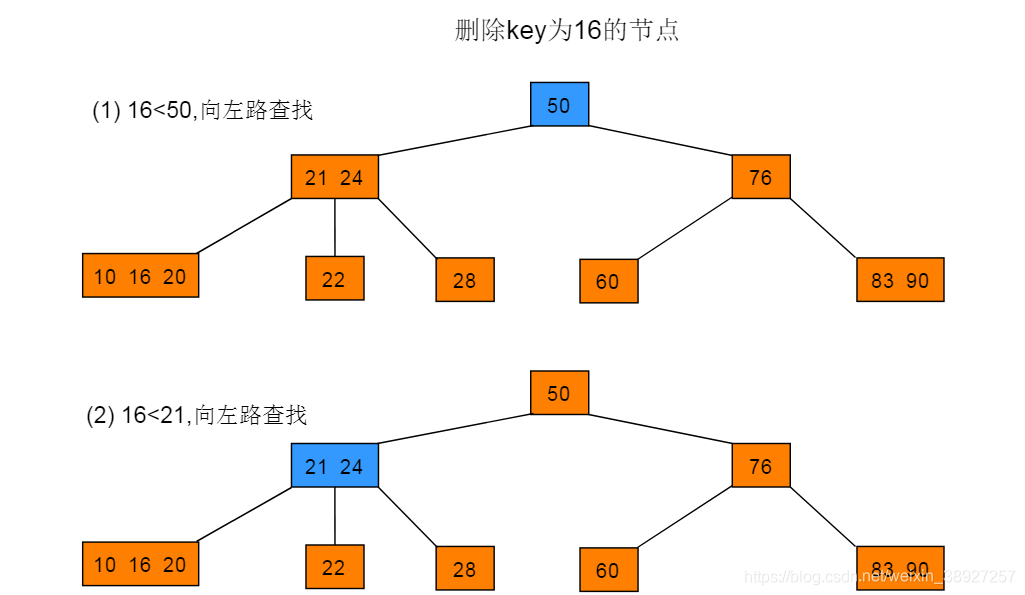
执行删除之前需要对删除key进行查找，若查找失败则无法删除。查找成功，才可删除key。删除节点情况有以下几种：

6.1 删除的节点不为2-节点

删除方法：若删除的节点不为2-节点，则将要删除的目标key直接删除即可。

图解：

6.2 删除非叶子节点

删除方法：当删除的节点是非叶子节点，无论待删除节点的key是多少个，先使用中序遍历找到待删除节点的后继节点，然后将后继节点与待删除节点位置互换，此时就将问题转化为删除节点为叶子节点（平衡树的非叶子节点中序遍历后继节点肯定叶子节点），如果该叶子是非2-节点，则与6.1节情形一样，如果该节点是2-节点，则跟后面的6.3情形一样。
图解：

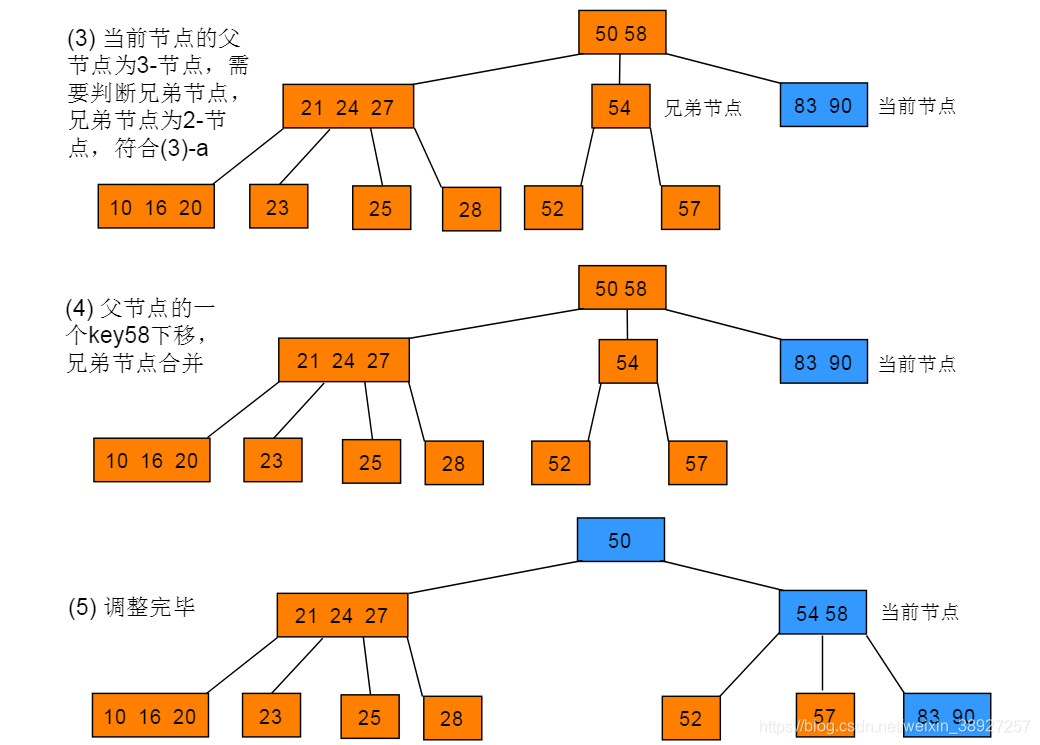
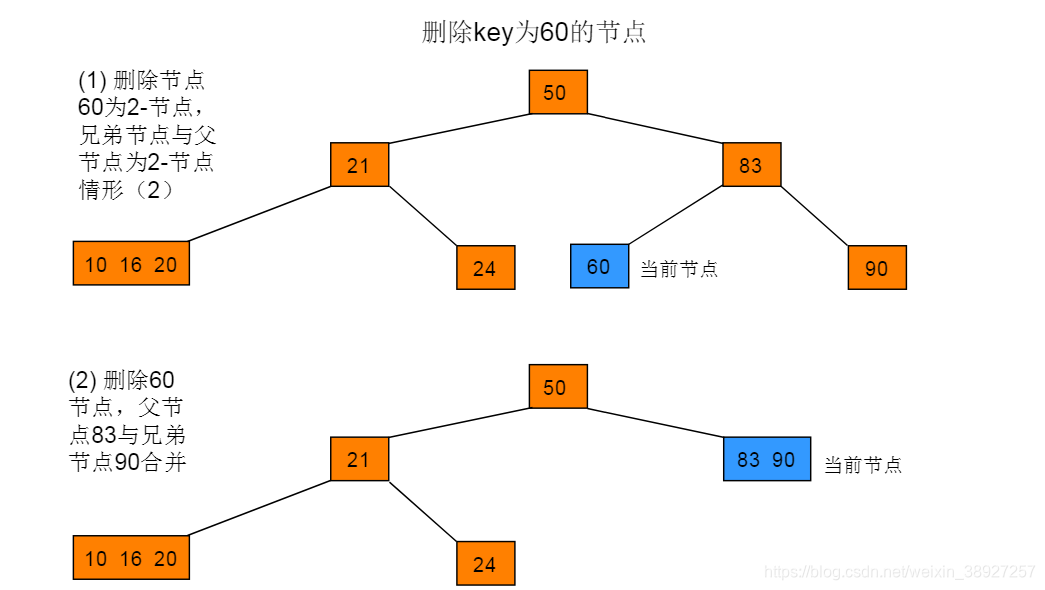
6.3 删除的叶子节点为2-节点

删除方法：当删除的叶子节点是2-节点，则将节点删除后，需要对树进行调整，调整规则如下：
（1）当前节点的父节点是2-节点，兄弟节点不为2-节点，则将兄弟节点的一个key上移成父节点，而父节点下移成子节点，此时树满足2-3-4树，完成调整。
（2）当前节点的父节点是2-节点，兄弟节点也为2-节点，则此时将父节点与兄弟节点合并，将合并后的节点看成当前节点，然后重复的判断，即判断合并后的当前节点的兄弟节点与父节点的情况，然后走对应的（1）（2）（3）处理，直到满足2-3-4树，完成调整。
（3）当前节点的父节点不为2-节点，即此时有两个或三个兄弟节点，此时需要根据相邻兄弟节点情形进行调整，规则如下：

（3）-a：若当前节点的相邻兄弟节点为非3个key，则父节点的一个key下移，与相邻兄弟节点合并，此时树满足2-3-4树，完成调整。
（3）-b：若当前节点的相邻兄弟节点为3个key，则父节点的一个key下移成1个key的节点，相邻兄弟节点的一个key上移与父节点合并，此时树满足2-3-4树，完成调整。

图解：
图解：
图解：

7 结语

本篇文章主要介绍了2-3-4树的性质，以及插入删除等操作。介绍2-3-4树的目的主要是为了为后续学习红黑树和B-树打下基础。

推荐阅读

数据结构——二叉树基础

数据结构——平衡二叉树（AVL树）（java版）

数据结构——2-3树